🚀个人主页：为梦而生~ 关注我一起学习吧！
💡专栏：机器学习 欢迎订阅！后面的内容会越来越有意思~
💡往期推荐：
【机器学习基础】机器学习入门（1）
【机器学习基础】机器学习入门（2）
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估（评估方法及性能度量原理及主要公式）
【机器学习基础】一元线性回归（适合初学者的保姆级文章）
【机器学习基础】多元线性回归（适合初学者的保姆级文章）
💡本期内容：Logistic回归和对数几率回归是同一个模型，是统计学习中的经典分类方法，属于对数线性模型。上一节讨论了如何使用线性模型进行回归学习，但若要做的是分类任务该怎么办？答案蕴涵在线性回归广义线性模型（假设函数）中：只需找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。超级基础的文章，赶紧收藏学习吧！！！

---

---

1 什么是对数几率回归

对数几率回归，也称为逻辑回归，是一种广义线性模型。在逻辑回归中，通过使用sigmoid函数，将线性回归的输出映射到0和1之间，表示样本属于某一类的概率。所以它属于分类模型。

逻辑回归模型的训练通常通过最大化似然函数来完成，常用的解决方法是使用梯度下降算法进行模型优化，通过迭代调整模型参数，使得模型的预测结果逐渐接近实际标签。

逻辑回归可以表示为一个关于θ的函数hθ(x)，即hθ(x) = P(y=1|x;θ)，表示给定特征x和参数θ的条件下，样本属于正例的概率。

由于它属于一个分类模型，所以它的输出应该具有分类的性质，于是，这里规定其输出永远在0，1之间。

---

2 假设函数

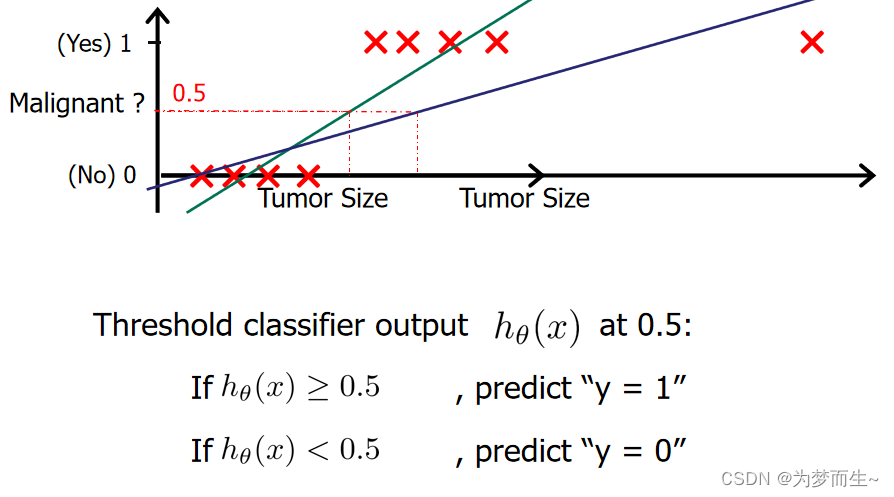
考虑二分类任务,其输出标记 y∈{0, 1}，而线性回归模型产生的预测值$h_{\theta }(x)$是实值，于是，我们需将实值$z$转换为 0/1值最理想的是“单位阶跃函数”(unit-step function)

但阶跃函数并不连续，于是我们希望找到能在一定程度上近似单位阶跃函数的“替代函数”(surrogate function)，并希望它单调可微对数几率函数(logistic function)正是这样一个常用的替代函数：

那么对数几率回归的假设函数应该将输出控制到0~1之间，于是就有了大名鼎鼎的sigmoid函数：

• 对于假设函数在对数几率回归的解释：

$h_{\theta }(x)$的作用是：对于给定的输入变量，根据选择的参数计算输出变量=1的可能性。即$h_{\theta }(x)$带有一定的概率含义。

例如，对于给定的x，通过已知的参数计算出 $h_{\theta }=0.7$,则表示有70%的概率y为正例.

若将$y$视为样本$x$作为正例的可能性，则 $1-y$ 是其反例可能性，两者的比值$\frac{y}{1-y}$称为"几率" (odds) ，反映了$x$作为正例的相对可能性. 对几率取对数则得到"对数几率" (log odds ，亦称 logit)

由此可看出，式(3.18) 实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率，因此，其对应的模型称为"对数几率回归" (logistic regression ，亦称 logit regression) .

---

3 决策边界

在对数几率回归中，我们预测：

当hθ(x)>=0.5
时，预测y=1.

当hθ(x)<0.5
时，预测y=0.

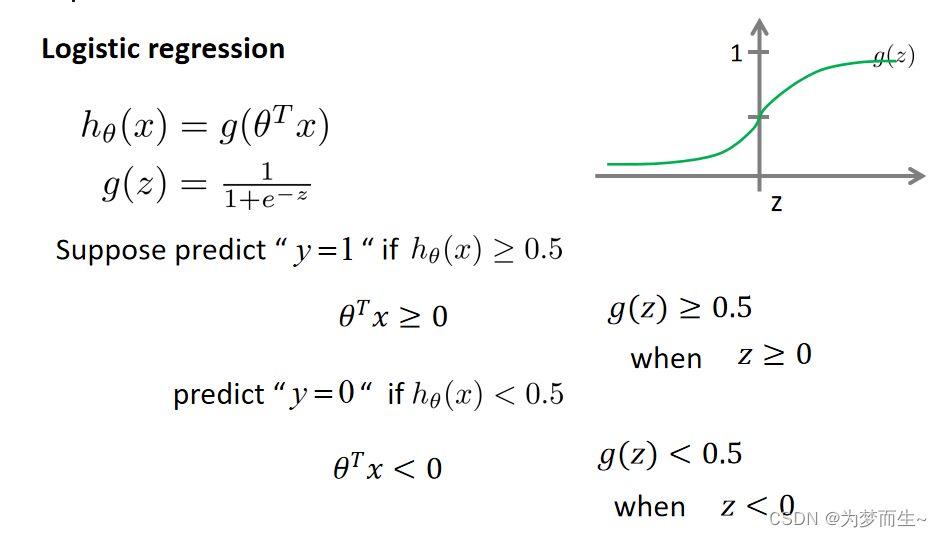
根据上面绘制的图像，我们知道：

当z>=0时，g(z)>=0.5

当z<0时，g(z)<0.5

• 举个例子

当参数$\theta$是向量$[-3,1,1]$。 则当$-3+x_1+x_2=0$时，模型将预测 y=1。我们可以绘制这条线便是我们模型的分界线，将预测为 1 的区域和预测为 0 的区域分隔开.

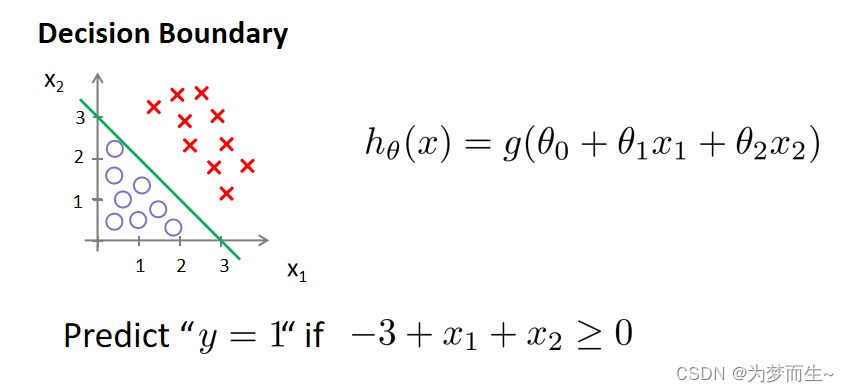
换句话说，大于这条线的部分预测y=0,小于这条线的部分预测y=0. 这条线就叫做决策边界。

---

4 代价函数

4.1 与线性回归模型的区别

对于线性回归，我们知道它的代价函数为$J(\theta )=\frac{1}{2m}{\Sigma }_{i=1}^m(h_{\theta }{x}^{(i)}-y^{(i)}{)}^2$, 我们可以对其进行梯度下降求最小值。其中可以用梯度下降最根本的原因在于它是一个凸函数，如下图所示

在逻辑回归中，如果还用和线性回归一样的代价函数的话，是求不到全局的最小值的，只能求到局部的最小值。这是因为，逻辑回归的假设函数变成了$h_{\theta }(x)=g({\theta }^{T}x)=g(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-{\theta }^{T}x}}$,将其带入上面的代价函数，可得到它的图像为:

由此我们知道，我们需要重新定义逻辑回归的代价函数。且这个代价函数一定是一个凸函数，否则不方便使用梯度下降求最小值。

4.2 重新定义代价函数

这里我们定义新的代价函数为：
$$J(\theta )=\frac{1}{m}{\Sigma }_{i=1}^{m}cost(h_{\theta }(x^{(i)}),y^{(i)})$$

这样分条件构建代价函数，可以使得当实际的 𝑦 = 1 且ℎ𝜃(𝑥)也为 1 时误差为 0， 当 𝑦 = 1 但ℎ𝜃(𝑥)不为 1 时误差随着ℎ𝜃(𝑥)变小而变大；当实际的 𝑦 = 0 且ℎ𝜃(𝑥)也为 0 时 代价为 0，当𝑦 = 0 但ℎ𝜃(𝑥)不为 0 时误差随着 ℎ𝜃(𝑥)的变大而变大。
由此可以保证它的输出用于分类

对其进行化简：

在得到这样一个代价函数以后，我们便可以用梯度下降法来求得代价函数取最小值时的参数了。方法和前面的线性回归求梯度下降差不多。

---

5 如何处理多分类问题

现实生活中，我们遇到的问题往往是很多类别的东西需要分类，所以如何利用二分类的模型解决多分类问题呢？

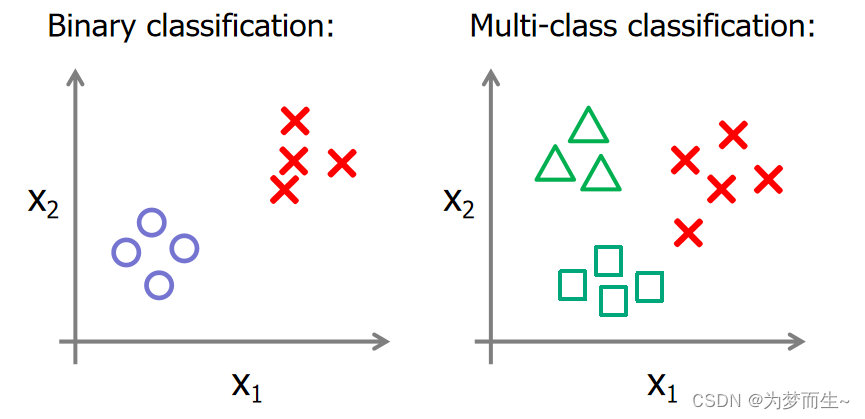
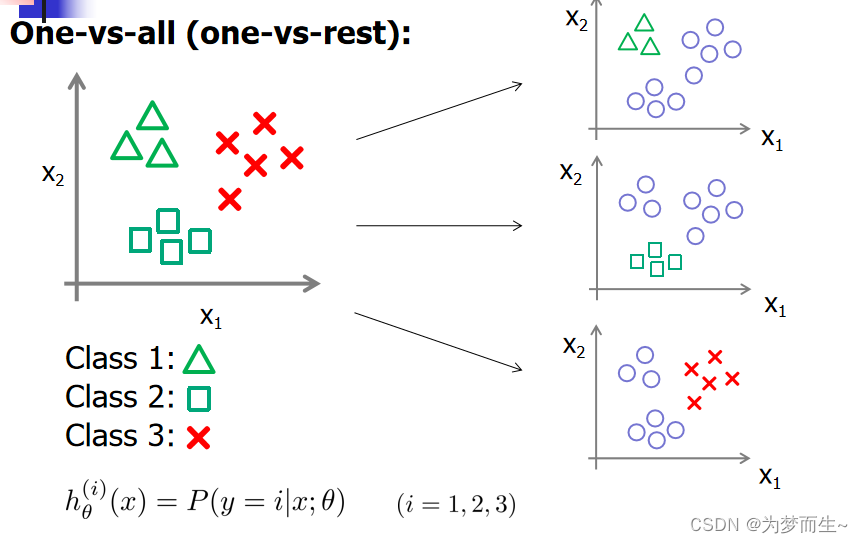
5.1 一对多法（one-versus-rest,简称OVR SVMs）

训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类，这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。

假如我有四类要划分（也就是4个Label），他们是A、B、C、D。
于是我在抽取训练集的时候，分别抽取

1. A所对应的向量作为正集，B，C，D所对应的向量作为负集；
2. B所对应的向量作为正集，A，C，D所对应的向量作为负集；
3. C所对应的向量作为正集，A，B，D所对应的向量作为负集；
4. D所对应的向量作为正集，A，B，C所对应的向量作为负集；

使用这四个训练集分别进行训练，然后的得到四个训练结果文件。在测试的时候，把对应的测试向量分别利用这四个训练结果文件进行测试。最后每个测试都有一个结果f1(x),f2(x),f3(x),f4(x)。
于是最终的结果便是这四个值中最大的一个作为分类结果。

• 评价：

这种方法有种缺陷,因为训练集是1:M,这种情况下存在biased.因而不是很实用。可以在抽取数据集的时候，从完整的负集中再抽取三分之一作为训练负集。

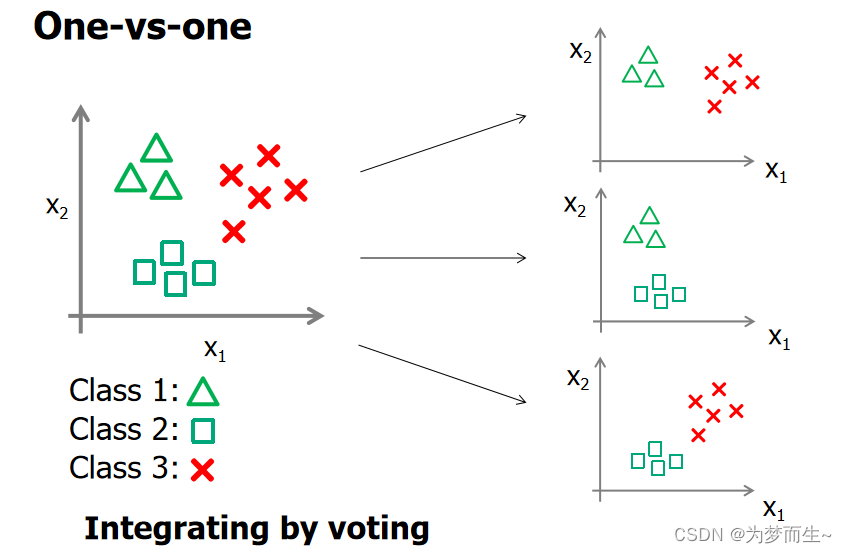
5.2 一对一的投票策略（One-vs-one）

分类器的选择：

• 将A、 B、C、 D四类样本两类两类地组成训练集， 即(A,B)、(A.C)、(A,D)、(B,C)、(B,D)、(C,D), 得到6个（对于n类问题，为n(n-1)/2个）SVM二分器。
• 在测试的时候，把测试样本又依次送入这6个二分类器， 采取投票形式， 最后得到一组结果。

投票是以如下方式进行的。

• 初始化：vote(A)= vote(B)= vote( C )= vote(D)=0。

• 投票过程：
  （1）如果使用训练集(A,B)得到的分类器将一个测试样本判定为A类，则vote(A)=vote(A)+1 ,否则vote(B)=vote(B)+ 1;
  （2）如果使用(A,C)训练的分类器将又判定为A类，则vote(A)=vote(A)+1, 否则vote( C )=vote( C )+1;
  （3）… ;
  （4）如果使用(C,D)训练的分类器将又判定为C类，则vote( C )=vote( C )+ 1 , 否则vote(D)=vote(D)+ 1。
  

• 最终判决：
  Max(vote(A), vote(B), vote( C ), vote(D))。
  如有两个以上的最大值，则一般可简单地取第一个最大值所对应的类