Day48 力扣动态规划 : 647. 回文子串 |516.最长回文子序列 |动态规划总结篇
- 647. 回文子串
- 第一印象
- 看完题解的思路
- dp
- 递推公式
- 初始化
- 递归顺序
- 实现中的困难
- 感悟
- 代码
- 516.最长回文子序列
- 第一印象
- 我的尝试遇到的问题
- 看完题解的思路
- dp
- 递推公式
- 初始化
- 实现中的困难
- 感悟
- 代码
- 动态规划总结篇
- 动态规划基础
- 背包问题
- 打家劫舍
- 股票问题
- 子序列问题
- 卡哥的dp结束语
- 我的结束语
647. 回文子串
动态规划解决的经典题目,如果没接触过的话,别硬想 直接看题解。
https://programmercarl.com/0647.%E5%9B%9E%E6%96%87%E5%AD%90%E4%B8%B2.html
第一印象
有点点难看起来,直接看题解把。
看完题解的思路
dp
这道题比较特殊,之前做的题,dp数组的定义一般都是题目求什么,就定义成什么。
这样的话这道题应该定义成过dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。
这道题的dp要定义成:dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
请看VCR:
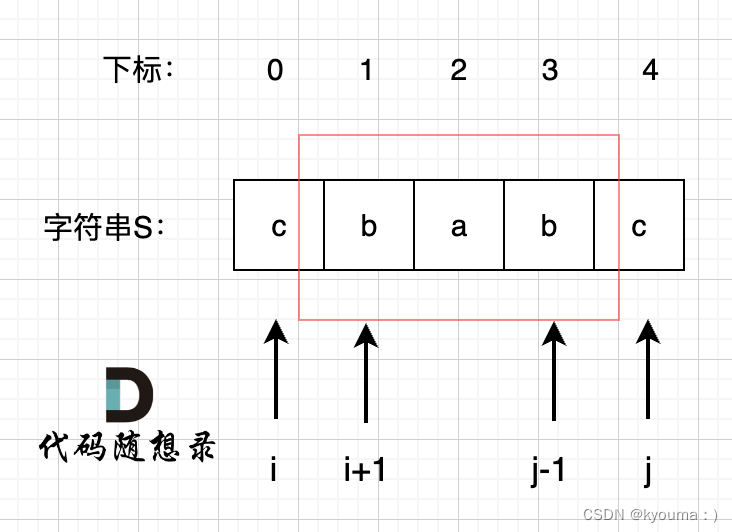
我们判断 i j的位置是不是相同的,如果是相同的,只要 i+1 到 j-1 是回文,那么 i 到 j 就是回文的。
所以我们可以找到一种递归关系:如果想要判断 [i, j] 是不是回文的,就要去看[i + 1, j - 1] 是不是回文的。
所以为了明确这种递归关系,我们的dp数组是要定义成一位二维dp数组。
递推公式
总体上分为两种:
- s[I] s[j] 两个元素相同
- s[I] s[j] 两个元素不相同
这种情况肯定就直接 dp[i, j] 是false了,肯定不回文。
两个元素相同的情况就比较复杂一些
情况一:i 和 j 指向同一个元素,一定是回文的。
情况二:i 和 j 是挨着的,i + 1 = j 。比如 aa,bb这样的情况,肯定是回文的。
情况三:i 和 j 距离超过 1 了,j - i > 1。比如 acba,a和a相同,然后就需要去判断cb是不是回文的
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
不用写不相等的情况了,因为初始化的时候就会默认都是 false。
初始化
全初始化为false,默认没有回文字串。
递归顺序
这道题的顺序就有说法了。
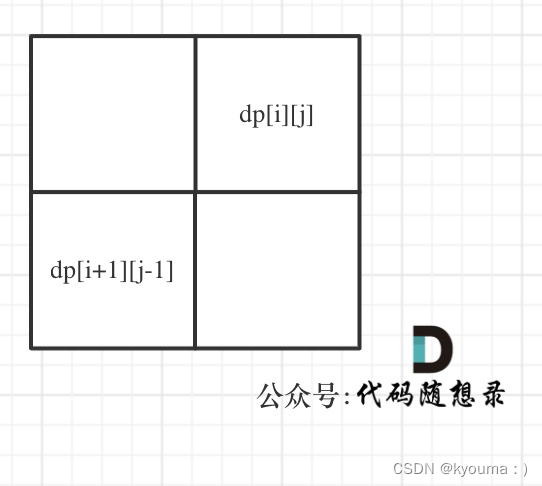
每个元素是用它左下角的元素推出来的。所以这个矩阵,行要从下向上遍历,列要从左到右遍历。
for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
for (int j = i; j < s.size(); j++) {
实现中的困难
无
感悟
I 和 j 基于 i+1 和 j-1 很容易理解。
但是我有点不理解倒序这个过程,他要求倒序只是从矩阵角度去看的。
从逻辑角度感觉看不出什么。
也能吧,如果正序的话,比如 i 是第二个元素,j 是第五个元素。他们相同,就需要看第三个到第四个元素是不是回文的。
但是呢,还没遍历到第三个元素,因为 i 才遍历到第二个元素。
如果倒序呢,i 遍历到第二个元素的时候就会遍历过第三个元素了。
感觉其实也是把矩阵里的事情用场景描述一下。
主要还是下面手动模拟体验一下,确实巧妙啊,用bcb的例子举例子,写在右边了。
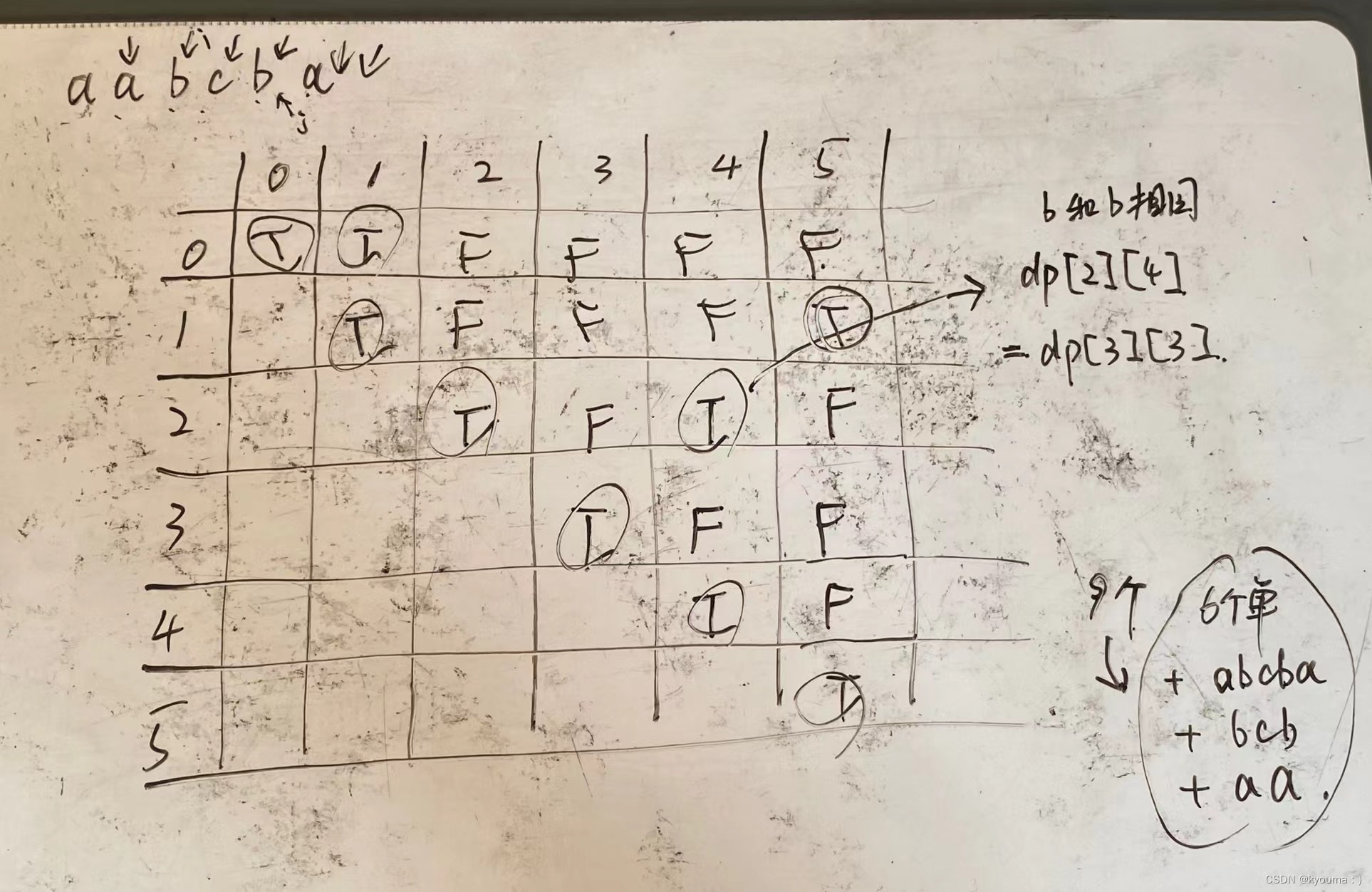
代码
class Solution {
public int countSubstrings(String s) {
int length = s.length();
//dp
int[][] dp = new int[length][length];
int count = 0;
//init
//func
for (int i = length - 1; i >= 0; i--) {
for (int j = i; j < length; j++) {
//当两个元素相同的时候才做,不相同就是默认的 0 不用管了
if (s.charAt(i) == s.charAt(j)) {
//距离 0 和 1 肯定ture
if ( i == j || i + 1 == j) {
dp[i][j] = 1;
count++;
} else {
//依赖于内部是不是回文
dp[i][j] = dp[i + 1][j - 1];
//是回文就count++
if (dp[i][j] == 1) count++;
}
}
}
}
return count;
}
}
516.最长回文子序列
- 回文子串,求的是回文子串,而本题要求的是回文子序列, 大家要搞清楚两者之间的区别。 https://programmercarl.com/0516.%E6%9C%80%E9%95%BF%E5%9B%9E%E6%96%87%E5%AD%90%E5%BA%8F%E5%88%97.html
第一印象
上一道题是连续的,这道题是子序列,可以不连续。
上一道题 i j 相等的话,就看 i + 1 和 j - 1 是不是回文,是的话 I j 就是回文的,然后用count记录回文数量。
这道题我觉得应该是i j 相等的话, 看 i + 1 到 j - 1 所有子串里面谁是回文的,求出回文子串里最大的长度。然后用length记录+2。
也可以直接在dp数组里赋值最大长度,长度为0代表不是回文,有长度就代表是回文,而且还有长度是多少。
诶,那上一道题是不是也可以dp数组赋值个数呢??等会试试
我先试试这道题。
我的尝试遇到的问题
我写出了代码,能跑过大部分测试用例,但是会超时,因为找内部最大的长度这个过程时间复杂度太高了。我相当于嵌套4层for循环了。
找内部最大这个事情,我是从最长递增子序列那道题影响过来的,每次从连续问题变成子序列问题的时候,我都想要去找内部最大,而连续就是找上一个就行。
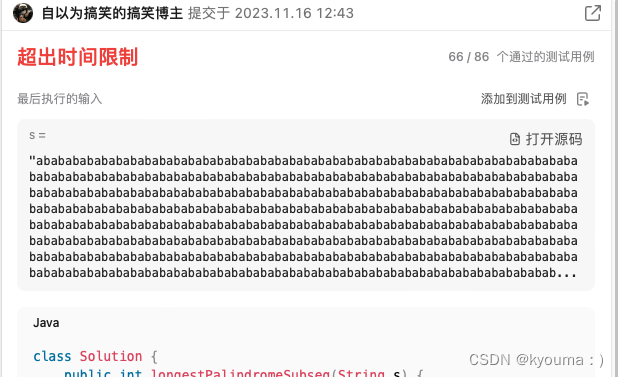
class Solution {
public int longestPalindromeSubseq(String s) {
// dp
int[][] dp = new int[s.length()][s.length()];
int length = 0;
//init
//func
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j)) {
if(i == j) {
dp[i][j] = 1;
length = Math.max(dp[i][j], length);
} else if (i + 1 == j) {
dp[i][j] = 2;
length = Math.max(dp[i][j], length);
} else {
int maxLength = 0;
//找内部最大的长度
for (int m = i + 1; m <= j - 1; m++) {
for (int n = m; n <= j - 1; n++) {
maxLength = dp[m][n] > maxLength ? dp[m][n] : maxLength;
}
}
//没找到回文的
if (maxLength == 0) {
dp[i][j] = 0;
} else {
//最大长度是内部最大的 + 2
dp[i][j] = maxLength + 2;
length = Math.max(dp[i][j], length);
}
}
}
}
}
// for (int i = 0; i < s.length(); i++) {
// for (int j = 0; j < s.length(); j++) {
// System.out.print(dp[i][j]);
// }
// System.out.println();
// }
//返回
return length;
}
}
看完题解的思路
dp
和我想的一样,记录这个情况下最长的长度。
递推公式
看一下题解吧,看看怎么优化呢。
我有点明白了,因为dp数组的含义是,i 和 j的时候,最长的回文子序列长度。
其实直接 dp[i][j] = dp[i + 1][j - 1] + 2; 就可以。但我为什么像上面那么做呢?
因为虽然dp数组定义为最长的长度,但是找到最长 这个逻辑、这个过程得有啊。
所以我就每次都去找内部的最长,再给到i j,这就是最长的。
但从dp数组含义出发,元素相同时,就可以像上面那样直接dp[i][j] = dp[i + 1][j - 1] + 2;
这样的话,找到最长的逻辑在哪呢?
答案是,在元素不相同的处理当中。
代码随想录的解释是
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
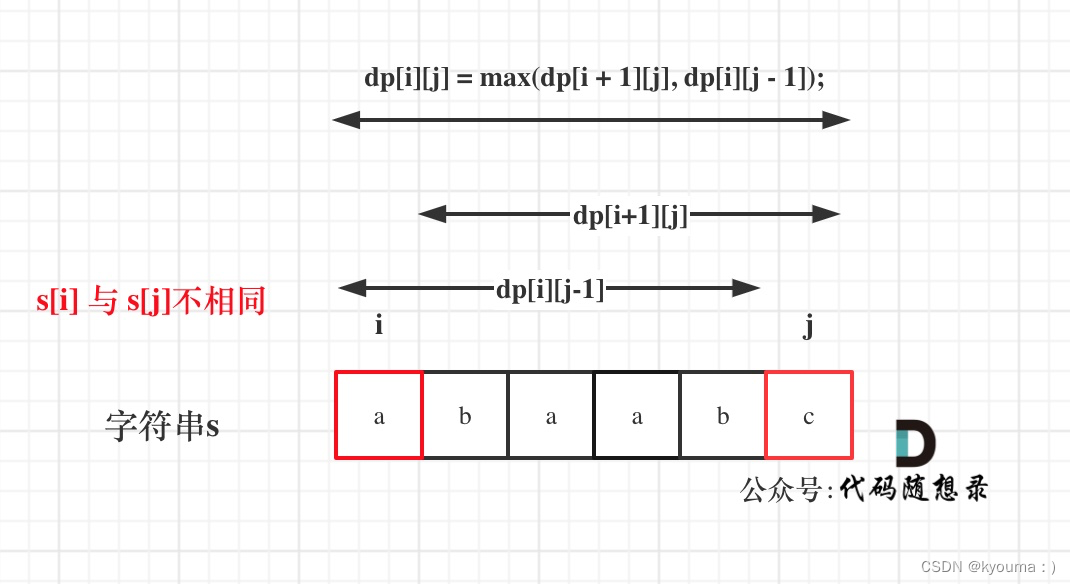
这样就把寻找最长的逻辑转移到元素不相同的处理当中了。
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
初始化
要对对角线元素初始化,因为每个元素自己肯定是回文的。我觉得这个也可以像上一道题一样处理
//如果相等
if (s.charAt(i) == s.charAt(j)) {
if(i == j) {
dp[i][j] = 1;
length = Math.max(dp[i][j], length);
} else {
dp[i][j] = dp[i + 1][j - 1] + 2;
length = Math.max(dp[i][j], length);
}
这里我就没初始化,而是在递推公式里初始化了算是。
实现中的困难
无
感悟
我觉得我明白连续子序列 ---->> 零散子序列的操作了
之前受那道最长递增子序列影响颇深,导致我每次都想找最大。
其实应该对不相等的情况进行找最大,而相等的时候按 dp 数组含义可以直接写出来了。
还有一道题也是类似的,是编辑距离里面的某一道,我记不住了,不过还行,有比较深的体会了。
代码
class Solution {
public int longestPalindromeSubseq(String s) {
// dp
int[][] dp = new int[s.length()][s.length()];
int length = 0;
//init
//func
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
//如果相等
if (s.charAt(i) == s.charAt(j)) {
if(i == j) {
dp[i][j] = 1;
length = Math.max(dp[i][j], length);
} else {
dp[i][j] = dp[i + 1][j - 1] + 2;
length = Math.max(dp[i][j], length);
}
} else {
//如果不相等
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
// for (int i = 0; i < s.length(); i++) {
// for (int j = 0; j < s.length(); j++) {
// System.out.print(dp[i][j]);
// }
// System.out.println();
// }
//返回
return length;
}
}
动态规划总结篇
https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E6%80%BB%E7%BB%93%E7%AF%87.html
总结可以直接看代码随想录了,我先做一下简单的总结。
动态规划感觉,一开始的一些题比较简单,属于用手就能模拟,比如爬楼梯那种,就给我一种数学归纳法的感觉。
后来到了背包问题,我觉得比较难理解,但我理解的还可以,做了不少总结。难在 dp 数组的理解、递推公式的理解、遍历顺序也会变。
然后打家劫舍,树形的打家劫舍不好弄,整体不算难。
股票问题,感觉很套路。难在 dp 数组的理解、递推公式的理解,遍历顺序就还好。
编辑距离,就是字符串上的一些操作,我也不理解为什么叫编辑距离。遍历顺序也是后面发生改变了。
最后就是回文子串的题。
dp问题给我的感觉就是每种问题五步走的难度是不一样的,大部分的都是难在
- dp数组的含义不会确定
- 递推公式关系找不到,这个我觉得是最关键的
- 遍历顺序不容易理解,其实遍历顺序也就正序逆序,两层for循环内外有没有区别(背包那里有区别)
- 初始化,绝大部分的初始化都是能一下子解决的,个别的偏难怪一些。
- 打印数组,这个其实就是通用操作了。
以上都是我过一遍脑子的回忆,下面去看看卡哥的总结。
动态规划基础
- 关于动态规划,你该了解这些! (opens new window)
- 动态规划:斐波那契数 (opens new window)
- 动态规划:爬楼梯 (opens new window)
- 动态规划:使用最小花费爬楼梯 (opens new window)
- 动态规划:不同路径 (opens new window)
- 动态规划:不同路径还不够,要有障碍! (opens new window)
- 动态规划:整数拆分,你要怎么拆? (opens new window)
- 动态规划:不同的二叉搜索树 (opens new window)
背包问题
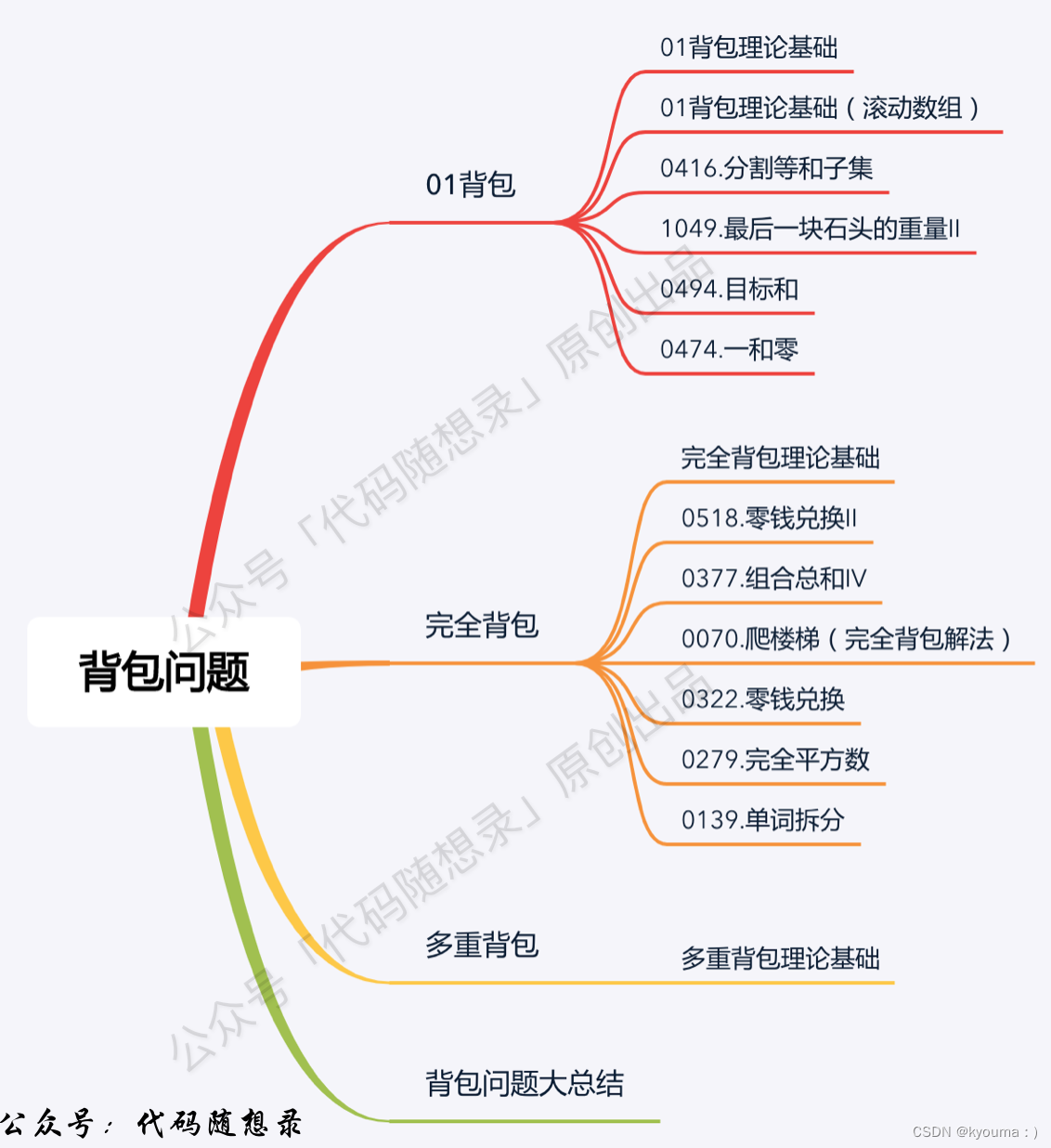
- 动态规划:关于01背包问题,你该了解这些! (opens new window)
- 动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)
- 动态规划:分割等和子集可以用01背包! (opens new window)
- 动态规划:最后一块石头的重量 II (opens new window)
- 动态规划:目标和! (opens new window)
- 动态规划:一和零! (opens new window)
- 动态规划:关于完全背包,你该了解这些! (opens new window)
- 动态规划:给你一些零钱,你要怎么凑? (opens new window)
- 动态规划:Carl称它为排列总和! (opens new window)
- 动态规划:以前我没得选,现在我选择再爬一次! (opens new window)
- 动态规划: 给我个机会,我再兑换一次零钱 (opens new window)
- 动态规划:一样的套路,再求一次完全平方数 (opens new window)
- 动态规划:单词拆分 (opens new window)
- 动态规划:关于多重背包,你该了解这些! (opens new window)
打家劫舍
- 动态规划:开始打家劫舍! (opens new window)
- 动态规划:继续打家劫舍! (opens new window)
- 动态规划:还要打家劫舍! (opens new window)
股票问题
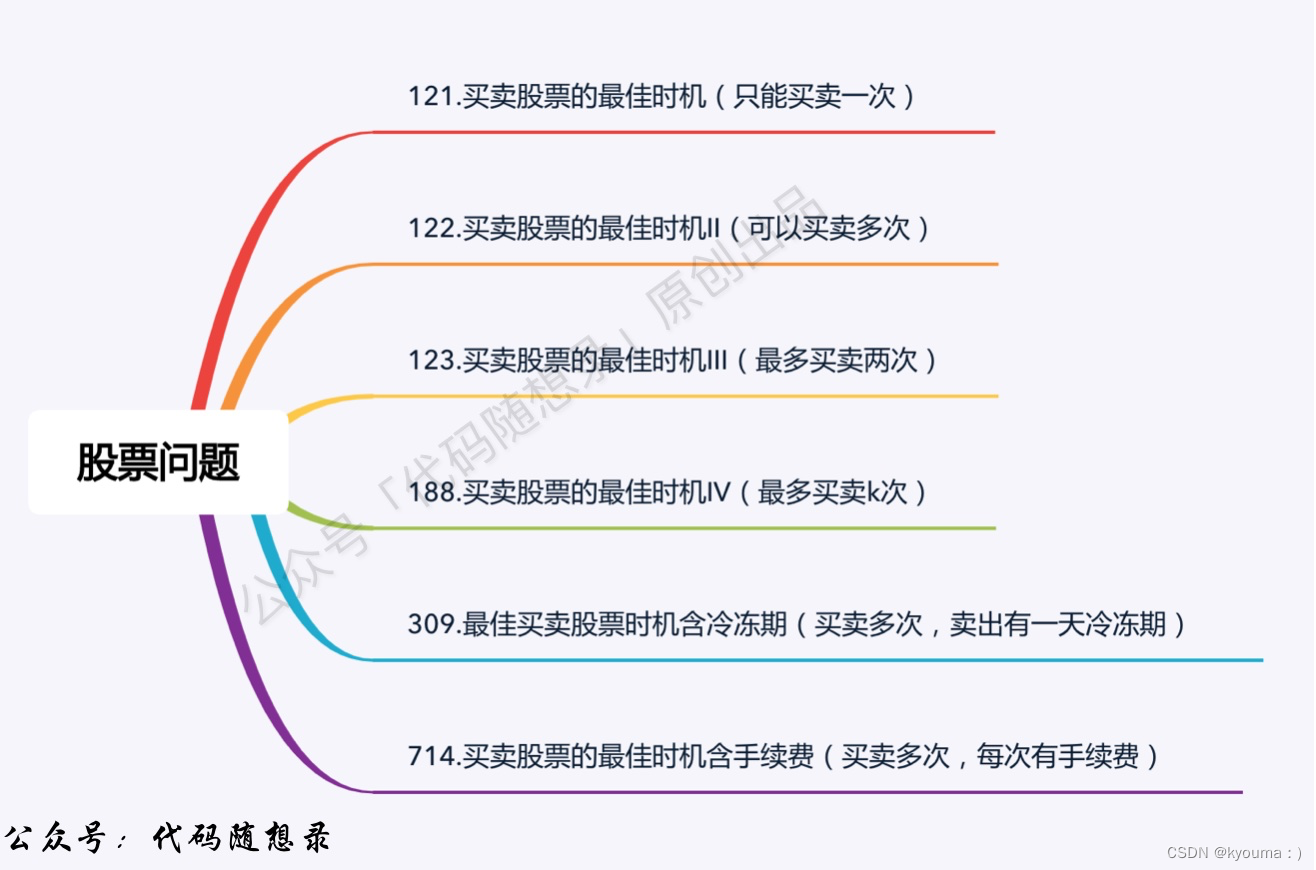
- 动态规划:买卖股票的最佳时机 (opens new window)
- 动态规划:本周我们都讲了这些(系列六) (opens new window)
- 动态规划:买卖股票的最佳时机II (opens new window)
- 动态规划:买卖股票的最佳时机III (opens new window)
- 动态规划:买卖股票的最佳时机IV (opens new window)
- 动态规划:最佳买卖股票时机含冷冻期 (opens new window)
- 动态规划:本周我们都讲了这些(系列七) (opens new window)
- 动态规划:买卖股票的最佳时机含手续费 (opens new window)
- 动态规划:股票系列总结篇 (opens new window)
子序列问题

- 动态规划:最长递增子序列 (opens new window)
- 动态规划:最长连续递增序列 (opens new window)
- 动态规划:最长重复子数组 (opens new window)
- 动态规划:最长公共子序列 (opens new window)
- 动态规划:不相交的线 (opens new window)
- 动态规划:最大子序和 (opens new window)
- 动态规划:判断子序列 (opens new window)
- 动态规划:不同的子序列 (opens new window)
- 动态规划:两个字符串的删除操作 (opens new window)
- 动态规划:编辑距离 (opens new window)
- 为了绝杀编辑距离,我做了三步铺垫,你都知道么? (opens new window)
- 动态规划:回文子串 (opens new window)
- 动态规划:最长回文子序列 (opens new window)
卡哥的dp结束语
关于动规,还有 树形DP(打家劫舍系列里有一道),数位DP,区间DP ,概率型DP,博弈型DP,状态压缩dp等等等,这些我就不去做讲解了,面试中出现的概率非常低。
能把本篇中列举的题目都研究通透的话,你的动规水平就已经非常高了。 对付面试已经足够
我的结束语
看来我的回忆也没什么错
因为dp内容太大了,这里也很难对所有的都进行一个总结。
如果有机会,我也学着去画画这种思维导图吧。
dp! 完结! 撒花!!!🎉