1.进制
A.二进制与各种转换
其实我们经常能听到2进制、8进制、10进制、16进制这样的讲法,那是什么意思呢?其实2进制、8进制、10进制、16进制是数值的不同表⽰形式⽽已。
⽐如:数值15的各种进制的表⽰形式:
15的2进制:1111
15的8进制:17
15的10进制:15
15的16进制:F
我们重点介绍⼀下⼆进制:
⾸先我们还是得从10进制讲起,其实10进制是我们⽣活中经常使⽤的,我们已经形成了很多尝试:
•
10进制中满10进1。
•
10进制的数字每⼀位都是0~9的数字组成。
其实⼆进制也是⼀样的:
•
2进制中满2进1
•
2进制的数字每⼀位都是0~1的数字组成。
那么
1101
就是⼆进制的数字了。
B.2进制转10进制
其实10进制的123表⽰的值是⼀百⼆⼗三,为什么是这个值呢?其实10进制的每⼀位是权重的,10进制的数字从右向左是个位、⼗位、百位....,分别每⼀位的权重是 1 , 10 , 100 ...
2进制和10进制是类似的,只不过2进制的每⼀位的权重,从右向左是:
1, 2 , 4 ...
如果我们现在知道31,如何转化为二进制呢?
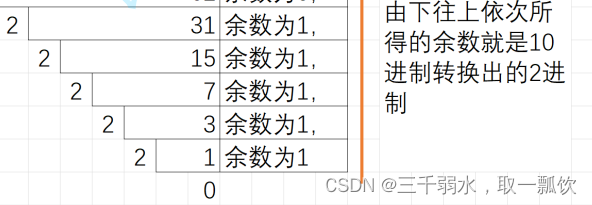
即结果为11111
C.2进制转8进制和16进制
8进制的数字每⼀位是0~7的,0~7的数字,各⾃写成2进制,最多有3个2进制位就⾜够了,⽐如7的⼆进制是111,所以在2进制转8进制数的时候,从2进制序列中右边低位开始向左每3个2进制位会换算⼀个8进制位,剩余不够3个2进制位的直接换算。
如:2进制的01101011,换成8进制:0153,0开头的数字,会被当做8进制

16进制的数字每⼀位是0~9,a ~f 的,0~9,a ~f的数字,各⾃写成2进制,最多有4个2进制位就⾜够了, ⽐如 f 的⼆进制是1111,所以在2进制转16进制数的时候,从2进制序列中右边低位开始向左每4个2进制位会换算⼀个16进制位,剩余不够4个⼆进制位的直接换算。
如:2进制的01101011,换成16进制:0x6b,16进制表⽰的时候前⾯加0x。
2. 原码、反码、补码
整数的2进制表⽰⽅法有三种,即原码、反码和补码。
有符号整数的三种表⽰⽅法均有符号位和数值位两部分,2进制序列中,最⾼位的1位是被当做符号 位,剩余的都是数值位。 符号位都是⽤0表⽰“正”,⽤1表⽰“负”。
正整数的原、反、补码都相同。
负整数的三种表⽰⽅法各不相同。
原码:直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。
反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。
补码:反码+1就得到补码。
反码得到原码也是可以使⽤:取反,+1的操作。
xdx要给大家举例子了,比如我们现在取一个整形变量,4个字节,一个字节有8个比特位,以一为例子:
原码:00000000000000000000000000000001
反码:00000000000000000000000000000001
补码:00000000000000000000000000000001
以-1为例子:
原码:1
0000000000000000000000000000001
反码:111111111111111111111111111111111110
补码:111111111111111111111111111111111111
对于整形来说:数据存放内存中其实存放的是补码。
为什么呢?
在计算机系统中,数值⼀律⽤补码来表⽰和存储。原因在于,使⽤补码,可以将符号位和数值域统⼀ 处理;同时,加法和减法也可以统⼀处理(CPU只有加法器)此外,补码与原码相互转换,其运算 过程是相同的,不需要额外的硬件电路。
所以进行相加时负数会转化为补码,这样子得到了1
00000000000000000000000000000000
前面的这个一会溢出,因为超过了32位,所以才会得到00000000000000000000000000000000
所以想到这个方法的人也是很牛牛的。省略了一个减法硬件,全部用加法算