t-product的matlab实现

news2024/11/29 8:39:13

t-product是一个比较好的概念，相对应于矩阵中的乘法。

定义如下

这里的 circ(A),MatVec(b) 的定义分别如下

这么定义的原因是为了映射到FFT域里面去，简化计算。

上面的一段摘录说明：直接按照定义来计算，会耗费大量的计算资源。因此，实际使用中是应用的另外一种方法“FFT”.

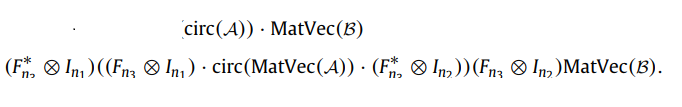
这两个等式是相等的，因为下面的公式其实施加了FFT变换之后又做了逆变换。注意发现上面的等式很有意思，结合文字好好看一下就有下面的计算方式。

计算方式

简单的说， A∗B 的过程如下

先把 A,B 模三展开，对每一个切片分别施加FFT, A¯(i),B¯(i)
切片对应相乘， A¯(i)∗B¯(i)
折叠回张量。

具体的原理，只知道可以这么做。具体理论分析，等待后续的知识（也在这篇论文上）。

Matlab代码实现

function C = tprod(A, B)
% tensor-tensor product of two 3-order tensors : C = A * B
% compute in the Fourier domain, efficiently
% A - n1 x n2 x n3 tensor
% B - n2 x l  x n3 tensor
% C - n1 x l  x n3 tensor
[n1, ~, n3] = size(A);
l = size(B, 2);
Af = fft(A, [], 3);
Bf = fft(B, [], 3);
Cf = zeros(n1, l, n3);
for i = 1 : n3
    Cf(:, :, i) = Af(:, :, i) * Bf(:, :, i);
end
C = ifft(Cf, [], 3);
end

fft(A,[],3)是标准的三阶张量沿模三做FFT的matlab操作.不必理会。

一个模拟数据验证

clc
clear all
%如何计算两个张量的t-product
X1 = 1:12;
X1 = reshape(X1,[3,4]);
X2 = 13:24;
X2 = reshape(X2,[3,4]);
X(:,:,1) = X1;
X(:,:,2) = X2;
Y1 = ones(4,3);
Y2 = ones(4,3);
Y(:,:,1) = Y1;
Y(:,:,2) = Y2;
C = tprod(X,Y)
C1 = X1*Y1 + X2*Y2
C2 = X2*Y1 + X1*Y2

结果如下

C
C(:,:,1) =
    92    92    92
   100   100   100
   108   108   108

C(:,:,2) =
    92    92    92
   100   100   100
   108   108   108

C1 =
    92    92    92
   100   100   100
   108   108   108

C2 =
    92    92    92
   100   100   100
   108   108   108