1.串的基本概念

• 串，即字符串 (String) 是由零个或多个字符组成的有限序列。一般记为S='a1a2.....·an'(n>=0)

S="HelloWorld!"
T='iPhone 11 Pro Max?'

其中，S是串名，单引号括起来的字符序列是串的值;a;可以是字母、数字或其他字符;串中字符的个数n称为串的长度。n =0时的串称为空串 。

• 子串:串中任意个连续的字符组成的子序列。
• 主串:包含子串的串。
• 字符在主串中的位置:字符在串中的序号。子串在主串中的位置:子串的第一个字符在主串中的位置。
• 串是一种特殊的线性表，数据元素之间呈线性关系
• 串的数据对象限定为字符集（如中文字符、英文字符、数字字符、标点字符等）
• 串的基本操作，如增删改查等通常以子串为操作对象。

2.串的基本操作

• StrAssign(&T, chars)： 赋值操作，把串T赋值为chars。
• StrCopy(&T, S):：复制操作，把串S复制得到串T。
• StrEmpty(S)：判空操作，若S为空串，则返回TRUE，否则返回False。
• StrLength(S)：求串长，返回串S的元素个数。
• ClearString(&S)：清空操作，将S清为空串。
• DestroyString(&S)：销毁串，将串S销毁（回收存储空间）。
• Concat(&T, S1, S2)：串联接，用T返回由S1和S2联接而成的新串。
• SubString(&Sub, S, pos, len)：求子串，用Sub返回串S的第pos个字符起长度为len的子串.
• Index(S, T)：定位操作，若主串S中存在与串T值相同的子串，则返回它再主串S中第一次出现的位置，否则函数值为0.
• StrCompare(S, T)：串的比较操作，参照英文词典排序方式；若S > T,返回值>0; S = T,返回值=0 (需要两个串完全相同) ; S < T,返回值<0.

3.串的存储实现 

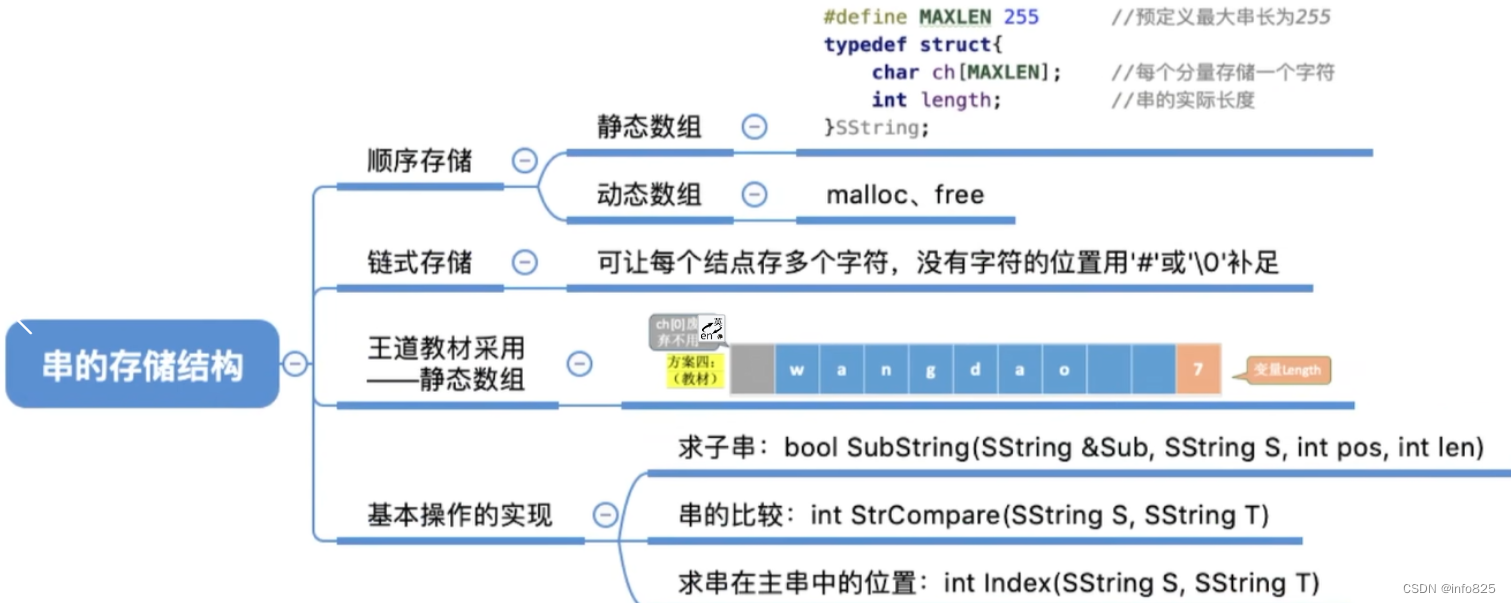
 3.1静态数组实现

静态数组实现(定长顺序存储)

#define MAXLEN 255   //预定义最大串长为255
 //静态数组实现（定长顺序存储）
typedef struct{
    char ch[MAXLEN];   //每个分量存储一个字符，每个char字符占1B
    int length;        //串的实际长度
}SString;

3.2 动态数组实现( 堆分配存储)

typedef struct{
    char *ch;          //按串长分配存储区，ch指向串的基地址
    int length;        //串的实际长度
}HString;
void Init(HString& S)
{
    S.ch = (char*)malloc(MAXLEN *sizeof(char));
    S.length = 0;
}

 3.3基本操作的实现

#define MAXLEN 255
 
typedef struct{
    char ch[MAXLEN];   
    int length;       
}SString;
 
// 1. 求子串
bool SubString(SString &Sub, SString S, int pos, int len){
    //子串范围越界
    if (pos+len-1 > S.length)
        return false;
    for (int i=pos; i<pos+len; i++)
        Sub.ch[i-pos+1] = S.ch[i];
    Sub.length = len;
    return true;
}
 
// 2. 比较两个串的大小
int StrCompare(SString S, SString T){
    for (int i = 1; i<S.length && i<T.length; i++){
        if(S.ch[i] != T.ch[i])
            return S.ch[i] - T.ch[i];
    }
    //扫描过的所有字符都相同，则长度长的串更大
    return S.length - T.length;
}
 
// 3. 定位操作,定位主串S中的子串T
int Index(SString S, SString T){
    int i=1;
    n = StrLength(S);
    m = StrLength(T);
    SString sub;        //用于暂存子串
 
    while(i<=n-m+1){
        SubString(Sub,S,i,m);
        if(StrCompare(Sub,T)!=0)
            ++i;
        else 
            return i;    // 返回子串在主串中的位置
    }
    return 0;            //S中不存在与T相等的子串
}
 

4.串的朴素模式匹配

• 串的模式匹配：在主串中找到与模式串相同的子串，并返回其所在主串中的位置。

4.1朴素模式匹配算法(简单模式匹配算法) 思想:

将主串中与模式串长度相同的子串搞出来，挨个与模式串对比当子串与模式串某个对应字符不匹配时，就立即放弃当前子串，转而检索下一个子串。

算法分析

• 若模式串长度为m，主串长度为n，则直到匹配成功/匹配失败最多需要(n-m+1)*m 次比较最坏时间复杂度: 0(nm)
• 最坏情况:每个子串的前m-1个字符都和模式串匹配，只有第m个字符不匹配。
• 比较好的情况:每个子串的第1个字符就与模式串不匹配
   

 4.2串的朴素模式匹配算法代码实现：

// 在主串S中找到与模式串T相同的子串并返回其位序，否则返回0
int Index(SString S, SString T){      
    int i=1, j=1;  
    while(i<=S.length && j<=T.length){    
        if(S.ch[i] == T.ch[j]){     
            ++i; ++j; 
        }else{        
           i = i - j + 2; j=1; 
        }   
    }   
    if(j>T.length) 
        return i - T.length;   
    else       
        return 0;
}


//引入辅助变量k,指向子串的首字符
// 在主串S中找到与模式串T相同的子串并返回其位序，否则返回0
int Index(SString S, SString T){   
    int k=1;    
    int i=k, j=1;  
    while(i<=S.length && j<=T.length){    
        if(S.ch[i] == T.ch[j]){     
            ++i; ++j; 
        }else{        
            k++; i=k; j=1; 
        }   
    }   
    if(j>T.length) 
        return k;   
    else       
        return 0;
}

时间复杂度：设模式串长度为m，主串长度为n

• 匹配成功的最好时间复杂度：
• 匹配失败的最好时间复杂度：
• 最坏时间复杂度：

5. KPM算法

算法思想

• 朴素模式匹配算法的缺点:当某些子串与模式串能部分匹配时，主串的扫描指针 i 经常回溯，导致时间开销增加。最坏时间复杂度。
• KMP算法:当子串和模式串不匹配时，主串指针i不回溯，模式串指针j = next[ j ]算法平均时间复杂度：。

5.1求模式串的next数组

相关概念：

串的前缀:包含第一个字符，且不包含最后一个字符的子串。

串的后缀:包含最后一个字符，且不包含第一个字符的子串。

最长公共前后缀（部分匹配值）：字符串的前缀和后缀的交集中最长的

前部分匹配值写成数组形式，就得到了部分匹配值表（partial match, PM)

使用PM表时，每当匹配失败需要去寻找它前一个元素的部分匹配值，这样使用起来有些不方便，所以将PM表右移一位，得到next数组，右移后第一位的空缺用-1填充，这样相当于将子串的比较指针回退到next[j+1] +1,有时为了使计算简介方便，会将next数组整体加1，如果next数组是从位序0开始的不需要加1

• next[j]的含义是，当第j个字符匹配失败，则跳转到子串的next[j]位置重新与主串当前值进行比较。

 KMP算法的核心是求next数组，下面给出next数组有三种求法 

5.1.1第一种next数组求法

首先看下面这个例子（1），当字符串匹配失败时，如果按照朴素版的话，模式串后移且两个指针初始化如（2）所示。但仔细观察模式串可以发现，绿框表示的是两个子字符串是相同的，那么只要将头子字符串直接移到 j 指针之前，那么依然能保证 j 指针前的字符串是匹配度如（3）所示。对照两者的区别可以发现，其中 i 指针是保持不变的，j 指针通过回溯去寻找相同的首字符串，通过这种思想做到了主串不回溯，时间复杂度可以大幅度降低至O(N+M)。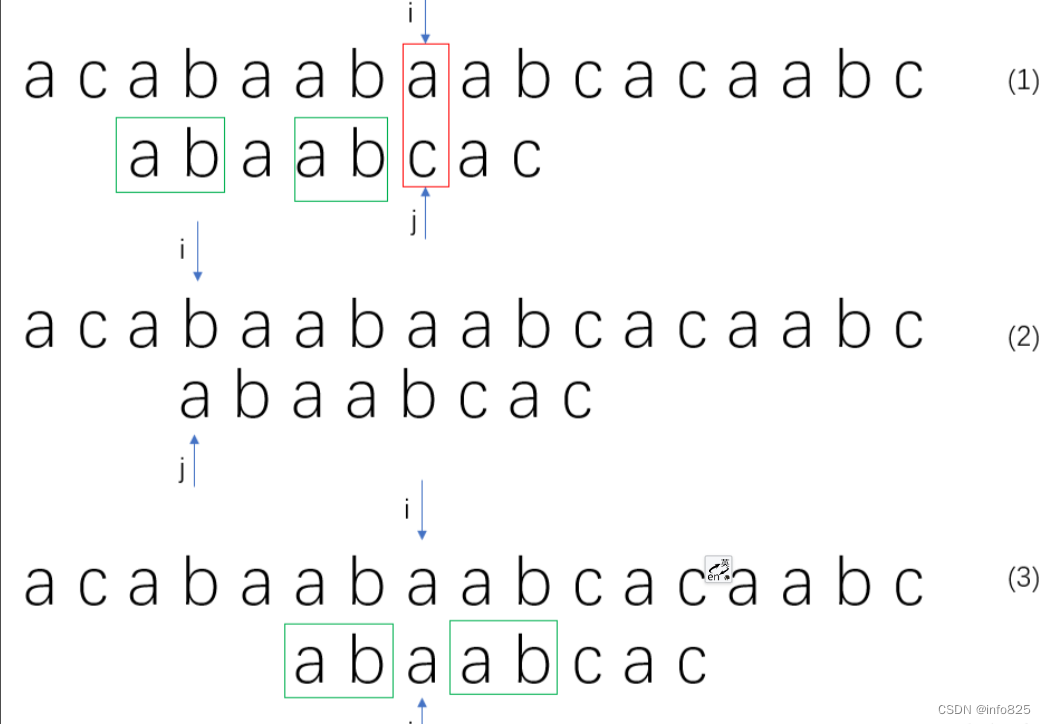

 对于如何让指针回溯的适合的位置，需要一个辅助数组next，next存放的是两字符串匹配时发生错误后指针 j 跳转的位置也就是态（1）转移到状态（3）。在计算next值之前，首先需要默认模式串从数组下标1开始存储，同样的next数组与存储数组相对应也是从1开始计算赋值为0。因为第一个字符如果匹配失败j指着跳转到0出也相当于模式串右移，下标0是用来判断没有匹配到的字符。如上模式串中的第一个c，虽然没有首字符串与它匹配，但是依然需要对它进行赋值，以便指针 j 匹配失败后制动到第一个字符的位置。匹配代码如下所示。

// 获取模式串T的next[]数组
void getNext(SString T, int next[]){ 
{
    for (int j = 0, i = 1; i < n;)
    {
        if (j == 0 || s[i] == s[j])
        {
            i++;        // 数组右移。存放当前指向元素的next
            j++        // 因为为了方便，数组整体加1
            next[i] = j;// 用下一时刻数组存放当前匹配的前缀位置+1
        }
        else    j = next[j];
    }
}

 根据上述代码模拟出模式串求next数组的过程，这个过程类似于模式串自己对自己进行KMP匹配，i指针及其之前的next值都已经求出来了，因此i指针指向的字符即使找不到匹配的字符，也可以让j指针回到0处赋值。

完整代码如下

// 获取模式串T的next[]数组
void getNext(SString T, int next[]){ 
{
    for (int j = 0, i = 1; i < n;)
    {
        if (j == 0 || T.ch[i] == S.ch[j])
        {
            j+, i++;
            next[i] = j;    // 用下一时刻数组存放当前匹配的前缀位置+1
        }
        else    j = next[j];
    }
}


// KPM算法，输出主串S中所有模式串T的位序，没有则输出0
void index_KMP(SString T, SString S)
{
    int i = 1, j = 1;
    bool flag = true;
    int next[T.length+1]; 
    getNext(T, next); 
    while (i <= S.length)
    {
        if (j == 0 || T.ch[j] == S.ch[i]) i++, j++;
        else    j = next[j];
        
        if (j > T.length)
        {
            cout << i - T.length - 1 << endl;    // 匹配成功，输出子串位置
            j--, i--;// 回退，寻找下一子串
            j = next[j];
            flag = false
        }
    }
    if (flag) cout << 0 << endl;
}
 
int main()
{
    SString S={"ababcabcd", 9};
	SString T={"bcd", 3};
    index_KMP(S, T);
    return 0;
}

5.1.2 第二种next数组求法

第一种next数组是存储回溯位置，在《算法导论》中提供了另一种next求法，next数组中存储的是最大的首字符串长度。如下代码所示，同样的从下标1开始存储，0为没有匹配字符，这里比较的是L+1和R的关系，当L+1与R不匹配返回让L继续回溯。当回溯完后还需要让L+1和R进行比较，因为可能原本字符匹配失败，但在回溯后匹配成功了。
 

void get_next()
{
    for (int l = 0, r = 2; r <= n; r ++ )
    {
        while (l != 0 && s[l + 1] != s[r])    l = next[l];
        if (s[l + 1] == s[r])    l++;
        next[r] = l;
    }
}

由于第二种KMP算法从始至终比较的都是L+1，回溯的是L，因此即使两个字符串匹配完成后，L和R指针依然指向两个字符串末字符，因此没必要确定位置，直接让L进行回溯即可。至于匹配过程，与上述匹配大同小异，需要额外注意L+1指针。

void index_KMP()
{
    for (int l = 0, r = 1; r <= m; r ++ )    //m为主串t的长度
    {
        while (l != 0 && s[l + 1] != t[r])  l = next[l];
        if (s[l + 1] == t[r]) l ++;
        if (l == n)    //可能存在多匹配成功
        {
            printf("%d ", r - n);
            l = next[l];
        }
    }
}

5.1.3第三种next数组求法

可以看到next[0]=-1，这个时候只需要让第一种计算出来的整体减1，

来自2024王道数据结构题P115第6题：

串“ababaaababaa”的next数组为（）

A、-1,0,1,2,3,4,5,6,7,8,8,8        B、-1,0,1,0,1,0,0,0,0,1,0,1

C、-1,0,0,1,2,3,1,1,2,3,4,5        D、-1,0,1,2,-1,0,1,0,1,2,1,1,2,3

按照第一种next数组求法结果为0 1 1 2 3 4 2 2 3 4 5 6，让每一个数都-1正好为答案：C 

或者直接手算最大公共前后缀然后整体右移

优化KMP算法

        在处理一些特殊的字符时，KMP算法还可以继续优化。如下案例，当模式串匹配遇到失败时，按照第一种匹配使得模式串后移一位。原本b！=a，在回溯后依然是b！=a……如果按照nextval数组，可以做到一步到位。

与原先的求next数组一样，nextval代码进行了两次比较，让后序的字符下标等于最初的下标，也就是上述的下标2~4全部都等于下标1的值。

void get_nextval(SString T, int nextval[])
{
	nextval[1]=0;
    for (int j = 0, i = 1; i < n;)
	{
		if (j == 0 || T.ch[j] == T.ch[i])
		{
			i++, j++;
			if (T.ch[j] != T.ch[i])	nextval[i] = j;
			else nextval[i] = nextval[j];
		}
		else	j = nextval[j];
	}
}

 next数组优化为nextval数组

首先nextval[0] = 1,然后从前往后依次求解，当遍历到的元素等于该元素的next元素时，此时next必然也不匹配，需要继续寻找可能匹配的，此时nextval[next[j]]早已求得（在前面），所以直接将nextval[j]赋值为nextval[next]，不需要再继续递归