🍎 博客主页:🌙@披星戴月的贾维斯
🍎 欢迎关注:👍点赞🍃收藏🔥留言
🍇系列专栏:🌙 蓝桥杯
🌙请不要相信胜利就像山坡上的蒲公英一样唾手可得,但是请相信,世界上总有一些美好值得我们全力以赴,哪怕粉身碎骨!🌙
🍉一起加油,去追寻、去成为更好的自己!
文章目录
- 前言
- 🍎1.中国象棋中的马的行动
- 题目描述
- 输入格式
- 输出格式
- 🍎2.Dijkstra求最短路 I(图论)
- 题目描述
- 🍎3.Dijkstra求最短路 II
- 🍎4. spfa求最短路
- 🍎总结
提示:以下是本篇文章正文内容,下面案例可供参考
前言
深度遍历算法(depth first search)俗称dfs和 广度优先遍历(broad first search)俗称bfs以及我们常听到的图论里面的最短路问题,借着这篇文章我们一起深入了解一下这些算法的逻辑和解法。
🍎1.中国象棋中的马的行动
题目描述
在中国象棋中,马的行动方式是“日”字形。假设我们有一个 8x8 的棋盘,棋盘的左上角是(0,0),右下角是(7,7)。马开始时位于给定的位置(x,y),你的任务是计算马需要多少步才能到达目标位置(a,b)。如果马不能到达目标位置,就返回-1。
注意:马只能按照“日”字形行动,即先向上或向下移动两步,然后向左或向右移动一步,或者先向左或向右移动两步,然后向上或向下移动一步。
输入格式
输入共两行,每行包含两个整数。第一行是马的初始位置(x,y),第二行是马的目标位置(a,b)。所有的整数都在0到7之间。
输出格式
输出一个整数,表示马到达目标位置需要的最少步数。如果不能到达,就输出-1。
输入输出样例
0 0;
7 7;
输出样例:
6
老规矩, 我们要养成一个好的写程序习惯,那就是先写思路,再写实现过程
解题思路:
首先,我们可以通过看数据范围大致判断这一题用到的算法,数据范围才8,可以支持dfs,bfs,dp等等各种算法,而且我们读题可以知道,🐎的行动方式是“日”字形,即可以画图得出它的方向图

即我们可以设置一个距离数组,通过bfs去枚举这八个方向,算出初始点到各个可能到达点的距离,我们通过队列来存储可能到达的下一个点,如果队列里面没有数字了就代表遍历结束,返回值。
代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
#define x first
#define y second
bool st[10][10];
int d[10][10];
int a1, b1, a2, b2;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2}, dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
int bfs(int x, int y)
{
queue<pii> q;
q.push({x, y});//把点放入队列
st[x][y] = true;//标记
while(q.size())
{
auto t = q.front();
q.pop();
if(t.x == a2 && t.y == b2) return d[a2][b2];//如果找到直接返回距离数组
for(int i = 0; i < 8; i++)
{
int ax = t.x + dx[i], ay = t.y + dy[i];
if(ax < 0 || ax > 7 || ay < 0 || ay > 7 || st[ax][ay] == true) continue;
st[ax][ay] = true;
d[ax][ay]=d[t.x][t.y]+1;
q.push({ax, ay});
}
}
return -1;//如果找不到就返回-1
}
int main ()
{
cin >> a1 >> b1;
cin >> a2 >> b2;
int t = bfs(a1, b1);
cout << t << endl;
return 0;
}
写法2:dfs深度搜索
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
#define x first
#define y second
bool st[10][10];
int dist[10][10];
int a1, b1, a2, b2;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2}, dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
void dfs(int x, int y)
{
if(x == a2 && y == b2) return;//判断结束条件
for(int i = 0; i <= 7; i++)
{
int tx = x + dx[i];
int ty = y + dy[i];
if(tx < 0 || tx > 7 || ty < 0 || ty > 7)
continue;
if(dist[tx][ty] > dist[x][y] + 1)
{
dist[tx][ty] = dist[x][y] + 1;
dfs(tx, ty);
}
}
return;
}
int main ()
{
cin >> a1 >> b1;
cin >> a2 >> b2;
memset(dist, 0x3f, sizeof dist); //先将方向数组置为0x3f
dist[a1][b1] = 0;
dfs(a1, b1);
if(dist[a2][b2] == 0x3f3f3f3f) cout << "-1" << endl;//如果没有搜到就输出-1
else cout << dist[a2][b2] << endl;//否则输出距离
return 0;
}
学习搜索我还推荐大家去看走迷宫和红与黑这两题,都是比较经典的。
🍎2.Dijkstra求最短路 I(图论)
题目描述
由于题目复制会乱码,所以博主干脆用图片代替。

图论问题和dp问题的区别
dp是选择下一个数(选择下一个状态)
图论是选择这个小的点去更新后继的节点

如下图例子:
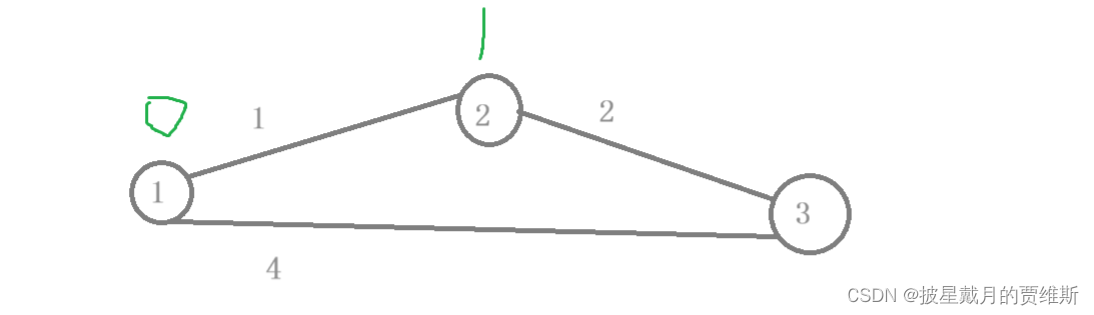
在这个例子中,我们把已经确定的最短的距离标为绿色,这时候我们t = 2这个节点,发现3这个节点 的距离到原点是4大于2 + 1,更新3和节点1的最短距离。
代码示例:
dist数组存储的是第一个节点到第 j个节点的距离是累加的
#include<bits/stdc++.h>
using namespace std;
//存稠密图用邻接矩阵
const int N = 510;
int n, m;
int g[N][N];
int dist[N];
bool st[N];
int dijkstar()
{
memset(dist, 0x3f, sizeof dist); // 1、先初始化距离
dist[1] = 0; //1号点到自己的距离为0
for(int i = 0; i < n; i++)
{
int t = -1;
for(int j = 1; j <= n; j++) //遍历所有点
{
if(!st[j] && (t == -1 || dist[t] > dist[j]))//如果j没有遍历过和t == -1或者t这点的距离>j的距离,更新t
t = j;
}
st[t] = true;
for(int j = 1; j <= n; j++)
{
dist[j] = min(dist[j], dist[t] + g[t][j]);//g的ab是a 到b 点的距离
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main ()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m; //n个点m条边
memset(g, 0x3f, sizeof g);
while(m --)
{
int a, b, c;
cin >> a >> b >> c;
g[a][b] = min(g[a][b], c);
}
int h = dijkstar();
cout << h << endl;
return 0;
}
🍎3.Dijkstra求最短路 II
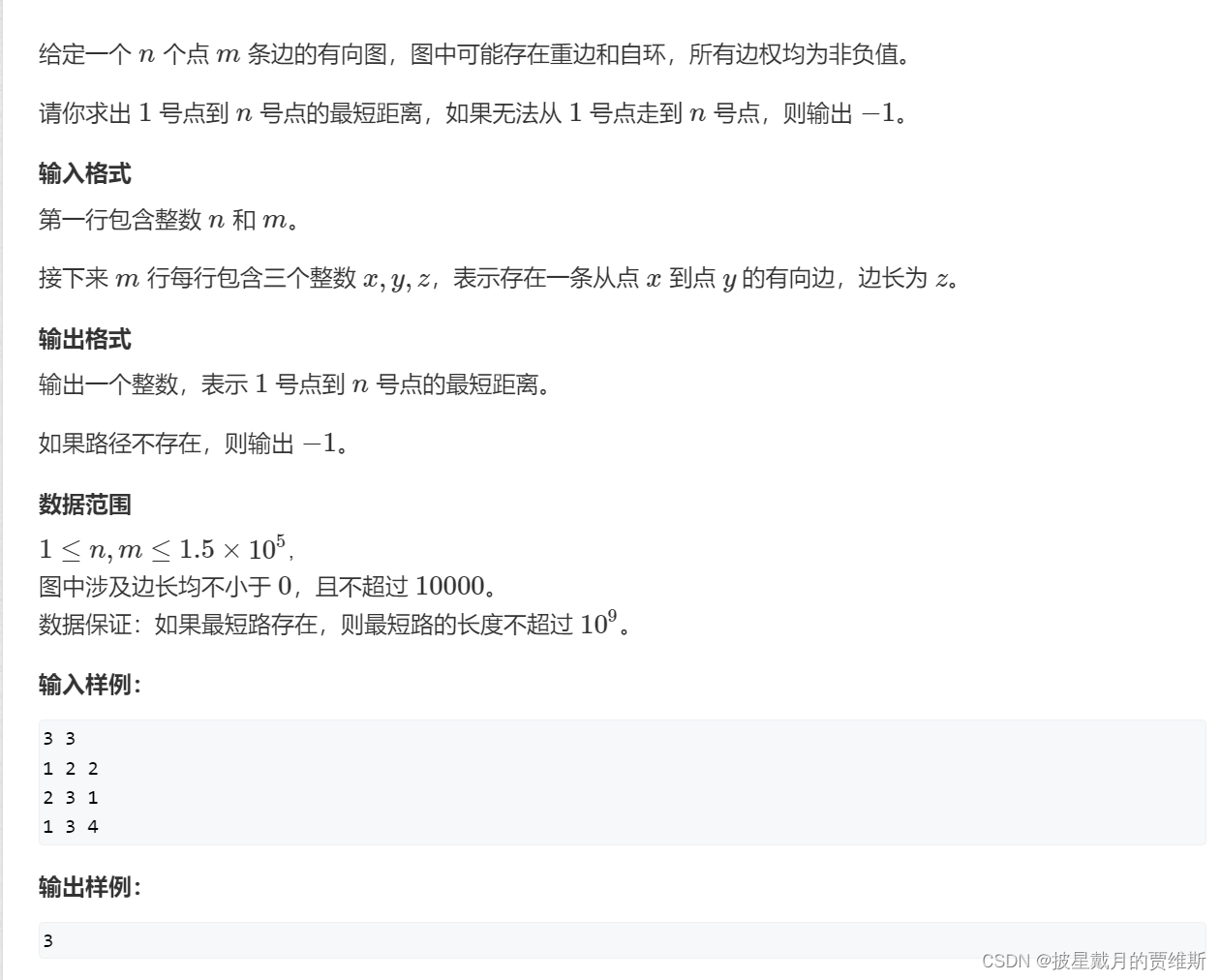
思路:n的数据范围从500 到了 1.5 * 10的五次方,数据量一下子变得很大,用邻接矩阵去存储很容易爆内存,而且会超时,所以要用邻接表去存。而且为了提高效率,我们要用优先级队列。
时间复杂度m*logn
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
#define x first
#define y second
typedef pair<int, int> pii;
int h[N], ne[N], e[N], idx, w[N];
int n, m;
bool st[N];
int dist[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] =idx++;
}
int dijkstart()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<pii, vector<pii>, greater<pii>> q;
q.push({0, 1}); //1号点,距离是0,编号是1
while(q.size())
{
auto t = q.top();
q.pop();
int ver = t.y, d = t.x;
if(st[ver]) continue; //说明遍历过了
st[ver] = true; //标记
for(int i = h[ver]; i!= -1; i = ne[i])
{
int j = e[i];//当前节点
if(dist[j] > d + w[i])
{
dist[j] = d + w[i];
q.push({dist[j], j});
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}
int main ()
{
memset(h, -1, sizeof h);
cin >> n >> m;
while(m --)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
int h = dijkstart();
cout << h << endl;
return 0;
}
🍎4. spfa求最短路
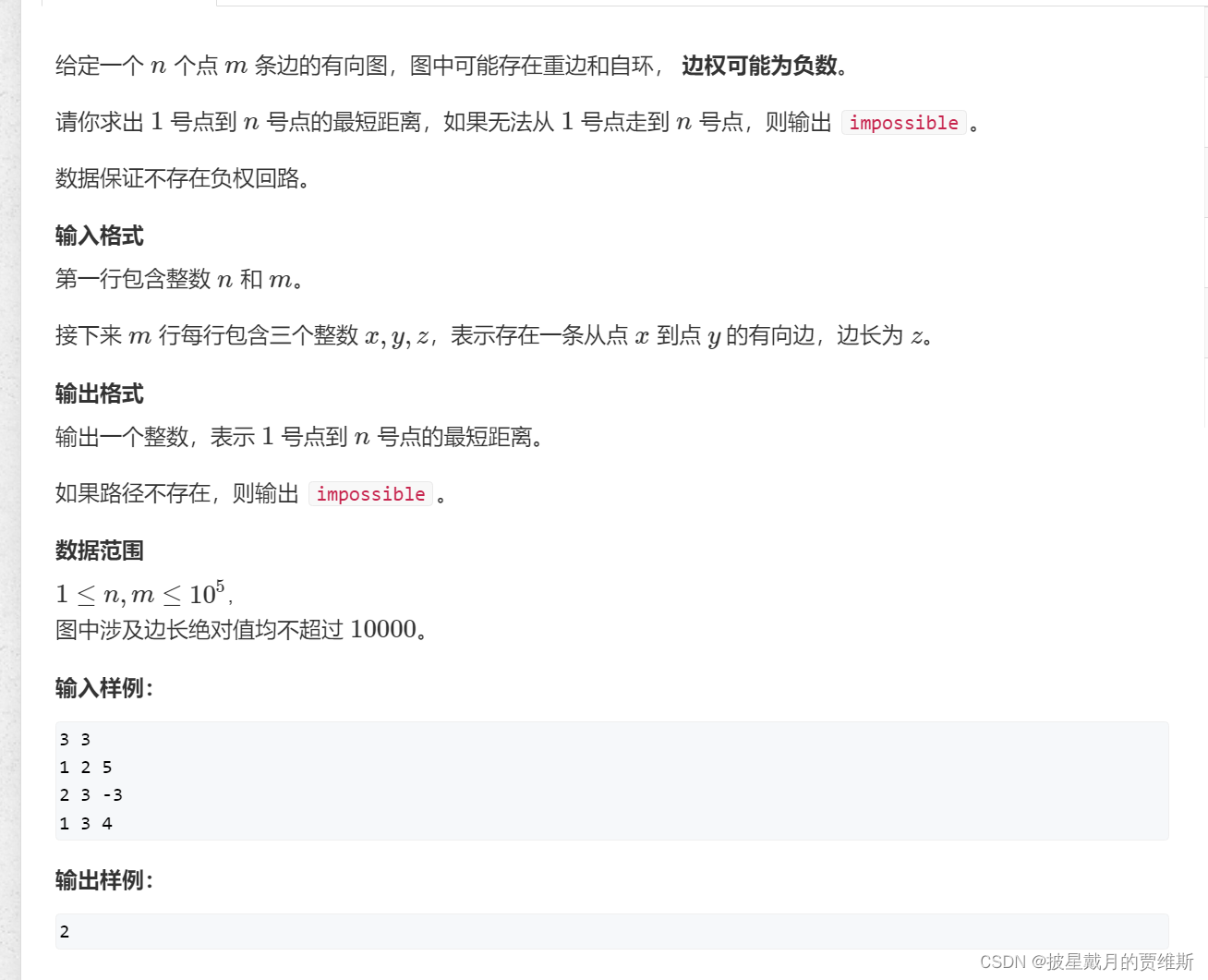
如果说边的距离全部都是正的,我们用dijkstart算法,那么如果存在负边权,那么我们可以采用spfa算法,而且spfa算法效率会高很多,时间复杂度是0(n * m)。同样,我们可以用spfa算法解决之前dijkstart算法的题,spfa的写法很像上一道题,利用邻接表去存储,然后利用队列把距离短的点存储起来,然后去更新后继节点。但是我可能会比较嫌弃邻接表写法比较复杂,我们可以用vector<结构体>这样的形式来存储图。
代码示例:
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
int n, m;
struct Node
{
int node;
int w;
};
int dist[N];
bool st[N];
vector<Node> g[N];//二维的数组
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q; //队列存储所有待更新的点
q.push(1); //把1号点放入队列
st[1] = true;// st数组存当前这个点是否在队列当中
while(q.size())
{
int t = q.front();//每次取出队头
q.pop();
st[t] = false;
//更新所有领边
for(int i = 0; i < g[t].size(); i ++)
{
int j = g[t][i].node;
if(dist[j] > dist[t] + g[t][i].w)
{
dist[j] = dist[t] + g[t][i].w;
if(!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return dist[n];
}
int main ()
{
cin >> n >> m;
while(m --)
{
int a, b, c;
cin >> a >> b >> c;
g[a].push_back({b, c});
}
int t = spfa();
if(t == 0x3f3f3f3f) cout << "impossible";
else cout << t << endl;
return 0;
}
🍎总结
本文和大家介绍了几题搜索和图论的题目,既帮助了自己复习,也希望对读者有所帮助!