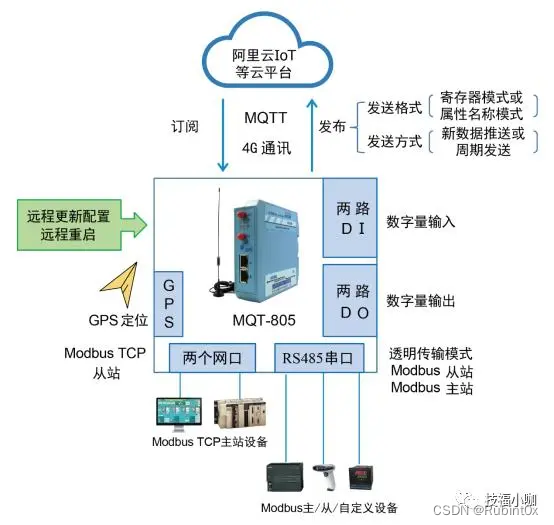
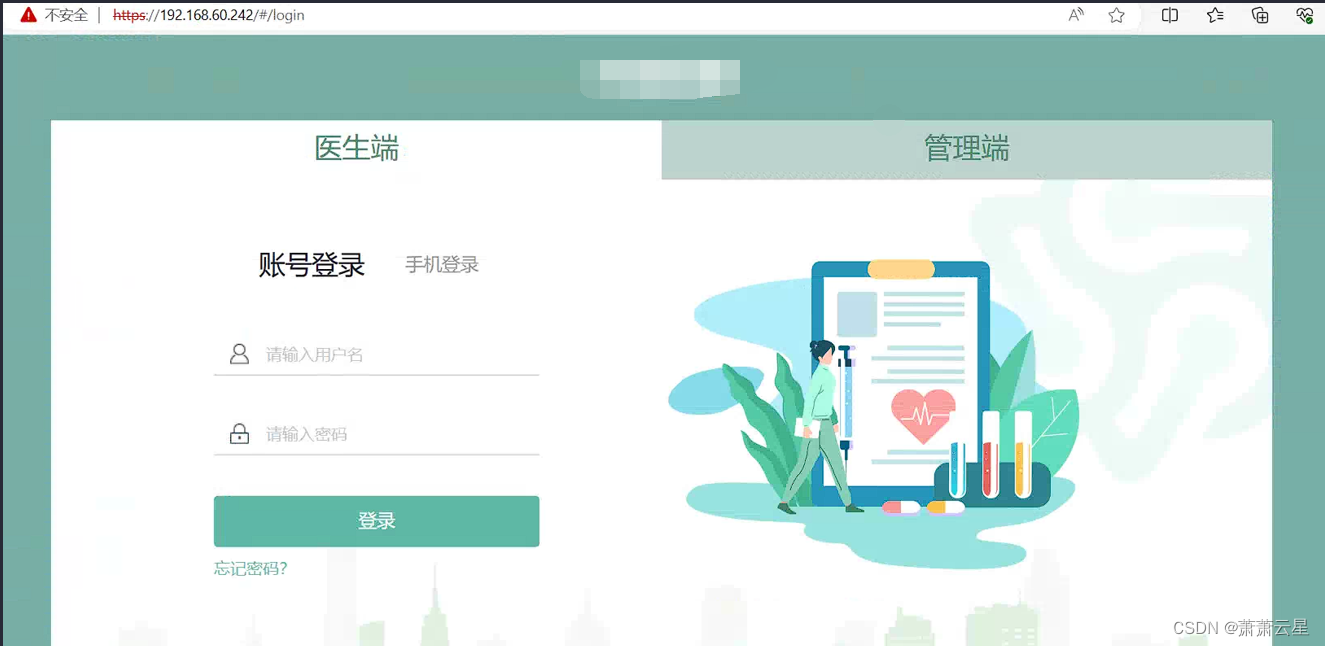
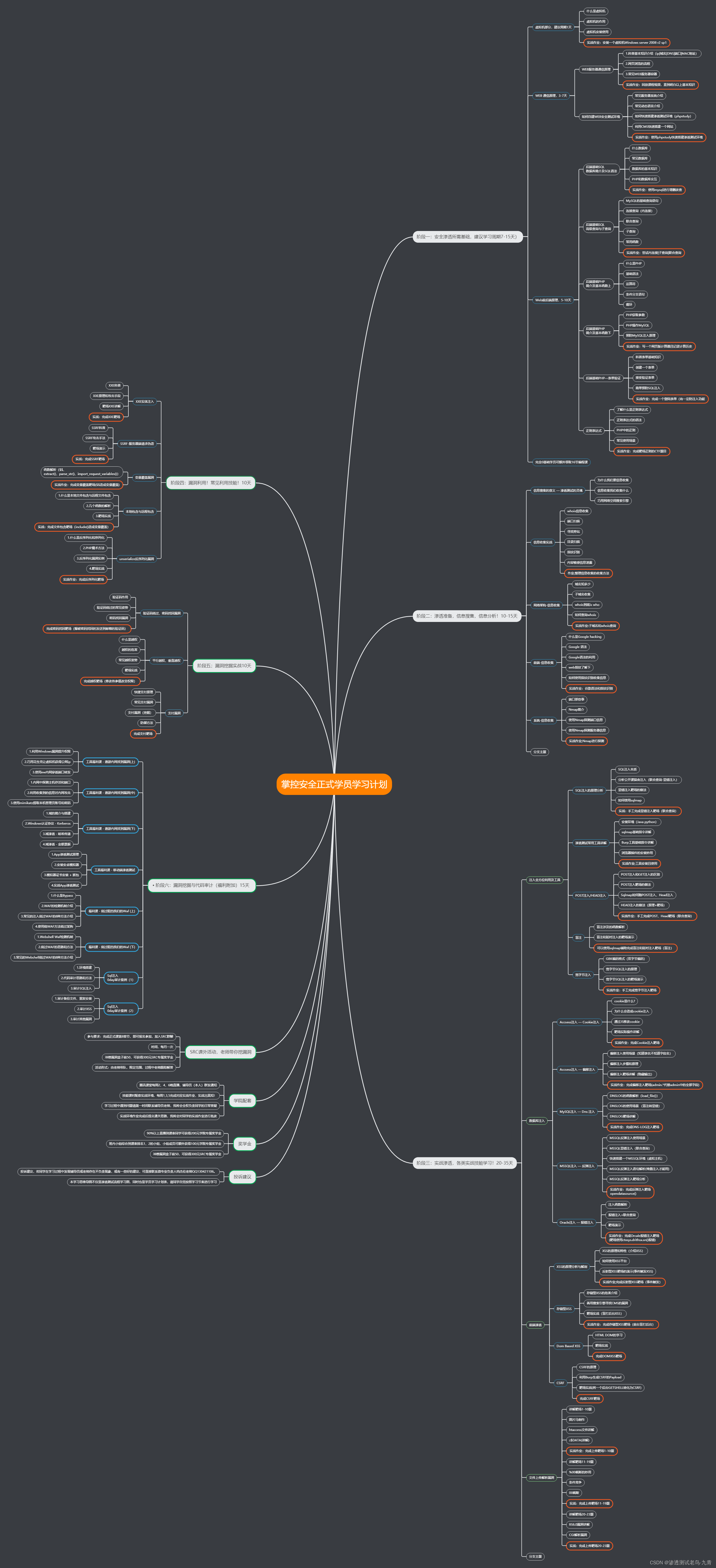
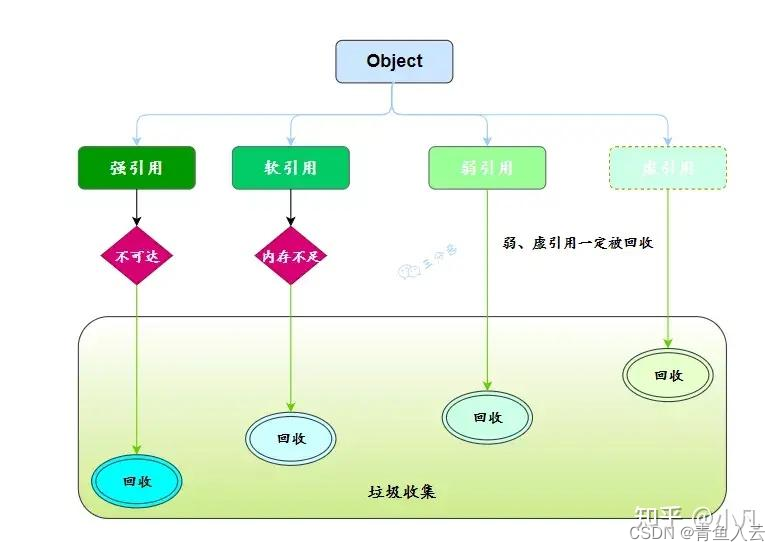
卷积神经网络应用领域
CV领域发展:

比赛中预测错误率的百分比,每年逐步下降。Human是人类肉眼的识别能力,2016年开始已经远高于人类肉眼死别能力,后面就取消了该方向的比赛了。
检测任务:

分类与检索:

分类:将图片分到对应类别。
检索:找到相似的图片。
还有图片重构、无人驾驶、人脸识别
卷积的作用
卷积网络与传统网络的区别:

输出的数据直接是三维的,还多了深度
整体架构:
输入层、卷积层、池化层、全连接层
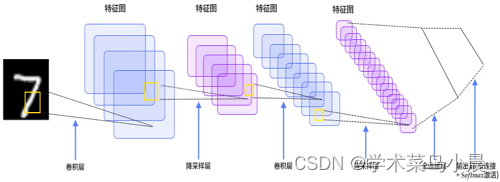
这里只有卷积层和池化层我们没有了解过
卷积做了什么事:

比如一个猫的图,眼睛鼻子特征和周围环境特征的重要性明显不一样,需要区别对待。先把图像进行分割(最左边),分割成多个小区域,提取其中一个小区域(第二个5×5×3),蓝色图的右下角3×3矩阵,大字体的值是X的值,而小字体的值是w权重,会不断循环获取最优的w权重和对应的值,并输出右边绿色的14(特征值)。
如果看了不理解,下面的具体计算方法一定能帮助你理解。
卷积的计算方法

input是输入,W0是第一层的权重,W1是第二层的权重,Output是输出
我们以input三个块(RGB三颜色)左上角3×3矩阵值 和 第二层W1来计算,内积是乘法再相加。
-
先来第一个(R颜色)左上角3×3:[0,0,0],[0,0,1],[0,0,1] 和 权重 [-1,-1,0],[-1,1,0],[-1,1,0]
(0*(-1) + 0*(-1) + 0*0)+(0*(-1) + 0*1 + 1*0)+(0*(-1) + 0*1 + 1*0)= 0 得出R颜色的左上角矩阵的值为0; -
第二个(G颜色) 左上角3×3矩阵值 和 第二层W1来计算
(0*1 + 0*(-1) + 0*0)+(0*(-1) + 1*0 + 1*(-1))+(0*(-1) + 0*0 + 2*0)= -1 -
第三个(B颜色) 左上角3×3矩阵值 和 第二层W1来计算
((-1)*0 + 0*0 + 1)+(0*1 + 2*0 + 0*1)+(0*0 + 0*(-1) + 0*0)= 0 -
最后再把三者结果相加并加上bias b1(偏值b)
0 + (-1) + 0 + 0 = -1
这级得到了output(0[:,:,1])中左上角的结果 -1。
卷积层的参数
卷积层涉及参数:滑动窗口步长、卷积核尺寸、边缘填充、卷积核个数

-
步长(移动多少个单元格):
-
步长为1的卷积:

移动一个步长,得到红色绿色特征值,移动的步长越小,特征值越多
-
步长为2的卷积:

移动两个步长,得到特征值越少
-
一般图像识别的用步长为1的,
-
-
卷积核尺寸:选择区域的大小,如上面是3×3的矩阵,可以选择4×4、5×5的,核尺寸越小,越细粒度提取,特征越多。
-
边缘填充:

+pad表示+1边缘,原本数据只有蓝色背景的部分(中间部分),而周围都是边缘增加的0,为什么这么做,滑动窗口时,边缘数据点明显滑动少,中间多,那能说明中间的就重要吗,为了使边缘的数据点也滑动多几次,就增加了这个边缘填充。文本分类中,有的文本有100个字,有的120字,不同长度无法训练,所以也会对其填充20个字,变成同样120的长度。
-
卷积核个数:最终计算的结果,要得到多少个特征图,个数多少,特征图多少。

-
卷积参数共享:即input使用的W部分的参数是共享的,卷积网络比之前的全连接大大减少了参数,不再需要每个对应的W。
池化层的作用
将原始input的所有数据,进行压缩

减少长宽以减少数据量的体积。
最大池化MAX POOLING:

-
如上图,从可选中,选出最大的值。为什么选择最大的值,因为前面是有权重W相乘的,还记得前面的W0和W1吗,如果计算完成得到的结果最大,那说明该结果是最重要的,所以这里选最大的,即挑最重要的。
-
体积也从上图的2×2矩阵变成4×4的矩阵
-
除了最大池化还有平均池化,不过平均池化基本没人用,既然有最好的结果,就应该拿最好的。
-
池化层没有结果任何计算,只是选最大的
整体网络架构
只有带参数的才能算层,Relu和池化不算

将一张图,通过不断卷积、池化、最后变成一条向量,接上全连接层,进行分类。
残差网络ResNet
深度网络遇到的问题:越大的层数理论上意味着越好,但实际是这样吗?下面是一组很早前测试的图
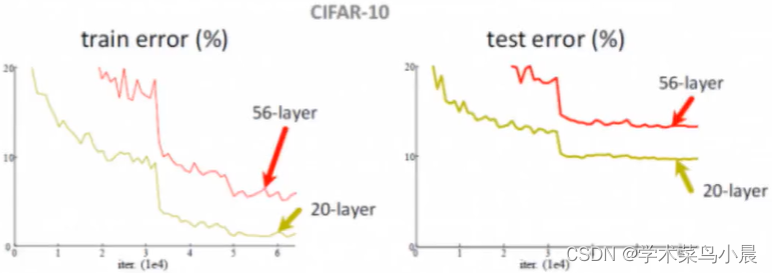
左边的训练集和右边的预测集都是20层的反而比56层的好,那么说明多出的36层起负作用。
解决方案:

我们还是跟原来一样增加层数,但在此基础上增加残差,也就是如果多的一层网络效果并不比上一层好,那么依然使用上一层的结果,可以看到X直接跳过了两层,这样就能保证了效果一定是越来越好的。
传统神经网络和Resnet的对比
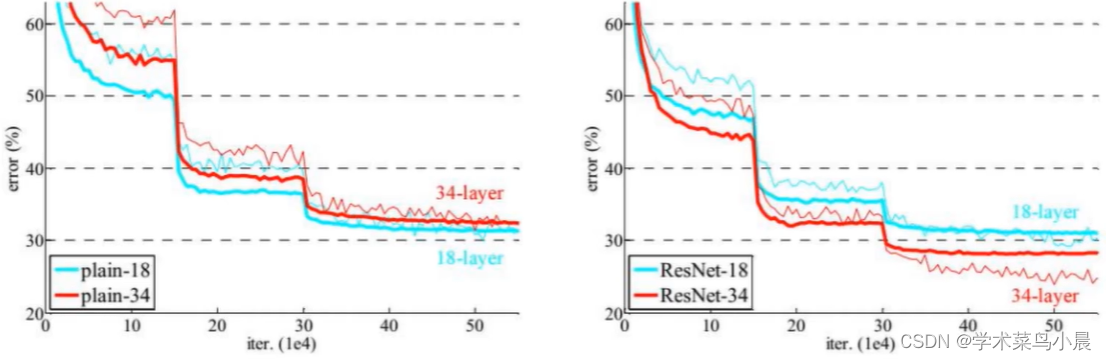
ResNet是层数越多效果越好。
下图是某个比赛中,冠军方案使用ResNet的层数是152层,第二名的22层有6.7的残差,而第一名的152层只有3.57的残差,相差近一倍的效果
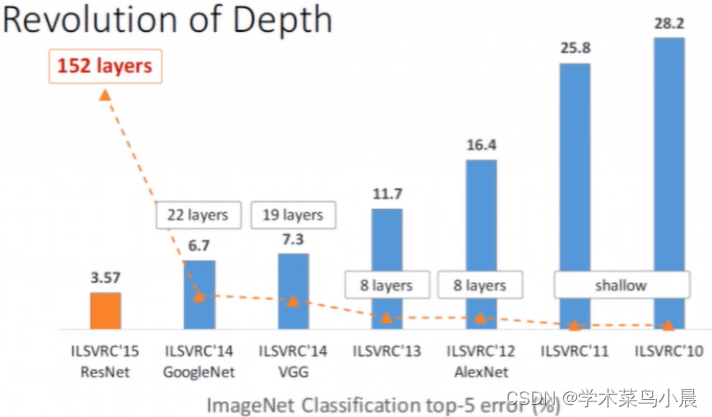
当然层数越多,可能收益越少,但是保证残差一定是小于等于之前的低层数,也就是结果一定是向好的发展。