一、说明
量子玻尔兹曼机(QBM)是量子物理学和机器学习的前沿融合。通过利用叠加和纠缠等量子特性的力量,QBM 可以同时探索多个解决方案,使其异常擅长解决复杂问题。它使用量子位(量子计算的构建模块)以传统计算机无法做到的方式处理信息。尽管仍处于早期阶段,QBM 在模拟量子系统、优化复杂场景和破译复杂数据模式等应用方面展现出了前景。尽管面临挑战,QBM 有潜力彻底改变计算并重塑我们处理复杂任务的方式。
二、玻尔兹曼机
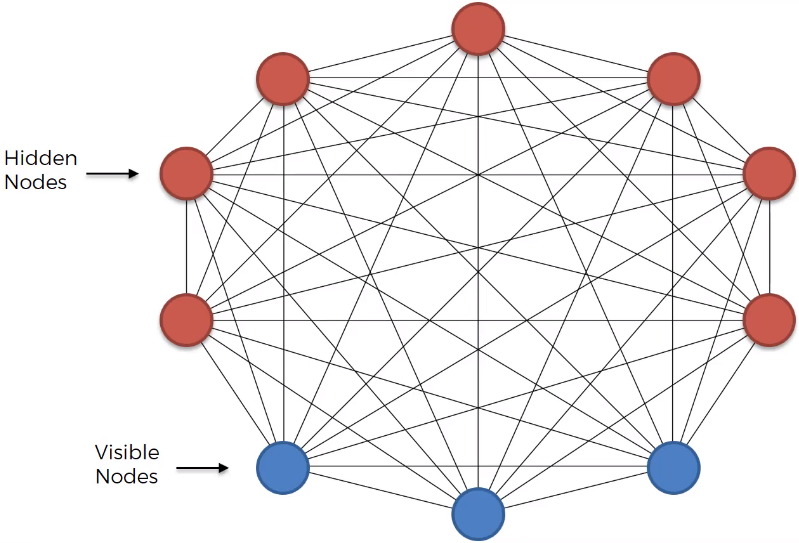
玻尔兹曼机是用于基于能量的机器学习的模型。这里显示的网络本质上是一个玻尔兹曼机,由隐藏节点和可见节点组成。隐藏节点充当潜在变量,在后台编码信息,而可见节点则确定模型的输出。在经典玻尔兹曼机中,这些节点可以是二进制的,表示 +1 或 -1 状态,类似于自旋变量。网络可以用能量函数来表示,其中节点之间的连接性反映在能量函数的加权项中。这适用于节点之间的连接和单个节点本身。为了将其与热力学联系起来,我们采用玻尔兹曼分布的概念。这些分布使我们能够根据可见节点相应的能量来计算其某些配置的概率。该概率是使用配分函数确定的,配分函数是所有可能的能量配置的总和,并确保我们具有有效的概率。
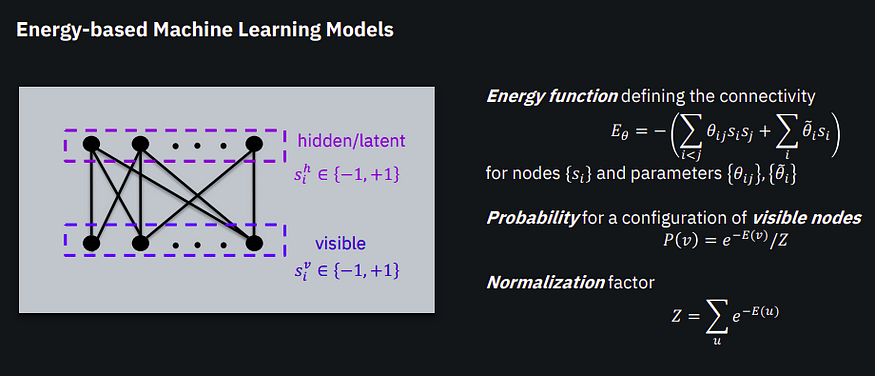
玻尔兹曼机设置的目标是训练能量函数中的参数,以便生成的概率代表概率分布。这种分布由训练数据和/或标签决定,具体取决于所使用的学习工具。所讨论的损失函数是交叉熵损失函数,它涉及从我们的模型中取概率的对数,将其与训练数据中的概率相乘,然后对所有可能的实例进行平均。
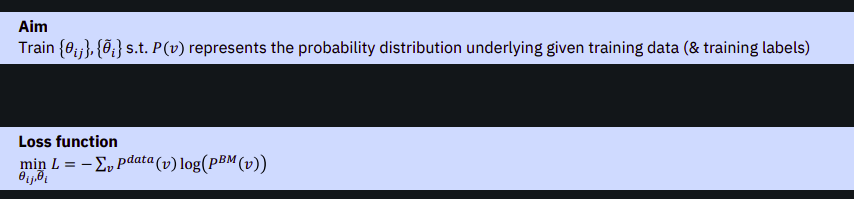
文本解释说,节点现在由信号表示,特别是作用于可见量子位的泡利算子(I、X、Y、Z)。模型输出由可见量子位的配置决定,并受到隐藏保利斯的影响。哈密顿量不是能量函数,而是基于网络连接性定义的。测量构型的概率是通过对量子吉布斯态的投影测量来确定的,由哈密顿量和配分函数编码。对于经典计算机来说,评估归一化因子可能具有挑战性。吉布斯状态对概率分布进行编码,并使用参数化量子电路进行近似。

文中解释说,为了训练哈密顿量的参数,采样概率需要准确地表示可能的权重分布。定义损失函数有两种选择:经典损失函数,其中测量量子态,采样概率确定损失;以及量子损失函数,其中经典概率映射到一级量子态,目标是将完整的吉布斯态与该量子态相匹配。后一个选项允许更自由地匹配概率分布,但这取决于具体目标。本研究的重点是第一个损失函数,它足以匹配经典分布并避免不必要的自由度训练。

这篇文章讨论了 VarQITE,这是量子虚时间演化的概念。它解释了如何使用基于加权泡利算子的 n 量子位哈密顿量,并探索了 Wick 旋转薛定谔方程。它提到算子缺少“I”并且需要归一化因子来维持量子态的 L2 归一化。这篇文章还描述了如何使用输入状态和参数化模拟将其合并到参数化量子电路中。使用变分原理来近似参数的演化。

为了执行参数演化,麦克拉克伦的变分原理用于最小化威克旋转薛定谔方程左侧和右侧之间的差异。这是在变分子空间内完成的,其中状态由 ansatz 表示。求解所得线性方程可提供 ansatz 参数的时间导数,该导数可以使用任意 ODE 求解器进行传播。麦克劳林的变分原理允许使用恒定架构量子电路来模拟状态演化。线性方程的右侧代表系统的能量梯度,而左侧代表 Fubini 研究度量,它描述了 ansatz 的信息几何。

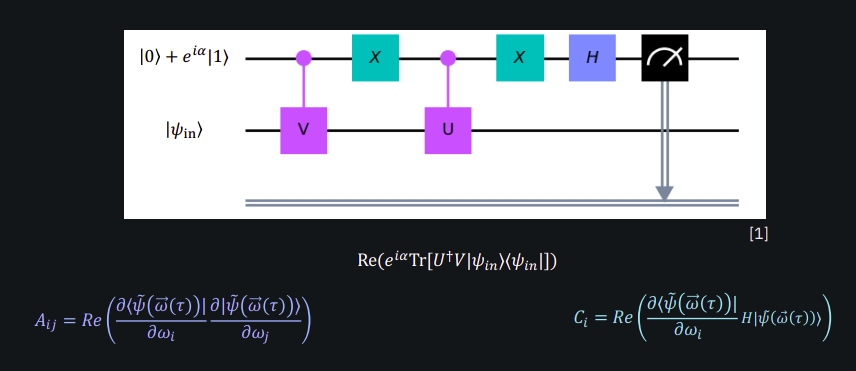
A 的评估在 ansatz 中的参数数量上是二次方昂贵的,并且在哈密顿量中的参数数量上是线性的。为了评估 A,使用了一种电路结构,其中涉及额外的量子位、受控操作和测量。A_ij 和 C_i 的项可以使用此电路结构以类似的形式重写,从而可以评估定义演化 ODE 的线性方程组所需的所有组件。
为了生成吉布斯状态,文本建议通过在子系统 B 上添加一个普通哈密顿量来扩展目标哈密顿量。初始状态以 n 个贝尔对给出,其中一部分在子系统 A 中,一部分在子系统 B 中。 out 子系统 B 给出子系统 A 的初始状态作为最大状态。然后使用 VarQITE 和哈密顿量 H_AB 来传播状态。再次追踪子系统 B 给出吉布斯状态的近似值。使用具有一个和两个量子位的简单示例在实际的量子计算机上测试了该方法。

文本讨论了哈密顿量和吉布斯状态,并解释了 ansatz 用于近似这些吉布斯状态。目标是确定每个时间步长的这些近似值与实际吉布斯态的接近程度,这是使用保真度作为量子态接近程度的度量来测量的。
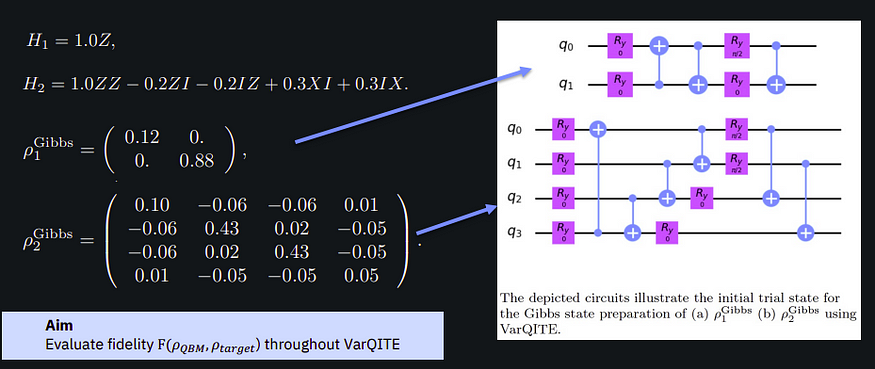
文本描述了两个哈密顿量 H1 和 H2 的训练,左侧使用较小的哈密顿量,右侧使用两个量子位门。显示了 IBMQ Johannesburg 20 量子位机器上精确模拟和测试的保真度演变。经过 10 个时间步长后,小量子位的保真度非常好,双量子位门的保真度约为 59%。对于这项小规模研究来说,这被认为是一个有趣且令人满意的结果。

本文研究了吉布斯状态的准备过程,随后重点介绍了量子玻尔兹曼机的教育。它提到了经典损失函数的使用以及使用吉布斯状态的概率计算。然而,计算损失函数的梯度并不容易。公式本身并不那么重要,重要的是绿色的正确项可以轻松有效地计算。如果某些交换关系不充分,则左侧红色项可能难以计算。以前的工作通常使用上限(例如 Golden-Thompson),而不是损失函数的实际梯度进行训练。
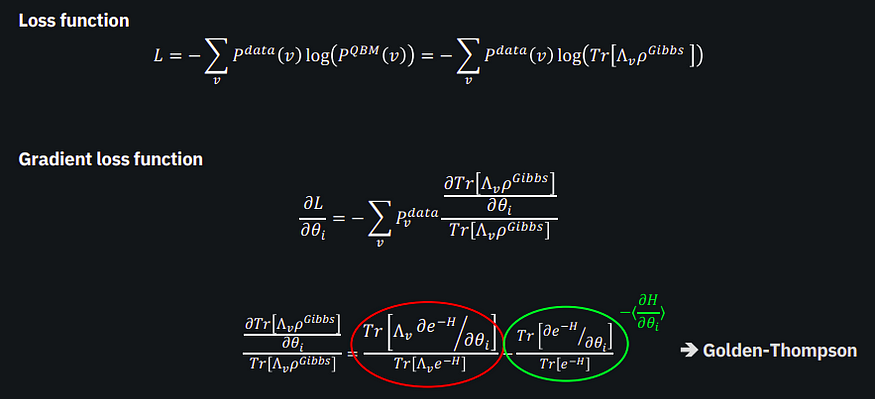
现在,将 VarQITE 用于我们的 QBM 的一个很酷的事情是,我们实际上可以利用我们的电路参数及其演化取决于我们的哈密顿参数这一事实。反过来,这使我们能够以最终的差异化来评估这些梯度。我们可以利用链式法则。

这篇文章讨论了操纵量子态时梯度的计算。它指出,计算与哈密顿参数相关的电路参数的梯度很简单,但找到与吉布斯状态相关的梯度则更加困难,因为它需要求解线性方程组。此项的时间导数可以通过吉布斯状态的准备来帮助扩展电路参数的梯度。这篇文章简要提到了颜色的使用,但没有提供额外的信息。

该算法首先初始化哈密顿量和初始参数。然后,它使用 VarQITE 准备吉布斯状态并获取自动微分项。插入项并计算相对于吉布斯状态的梯度。这允许评估损失函数梯度,用于更新哈密顿参数。重复这个过程直到满足终止标准以学习一个好的模型。
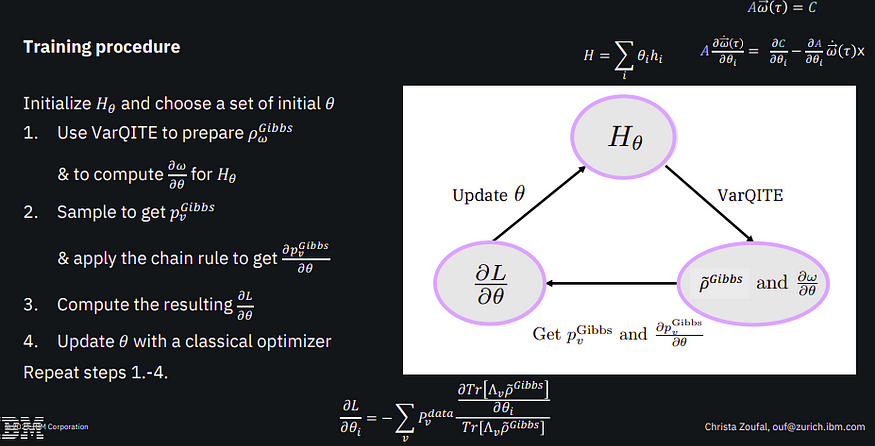
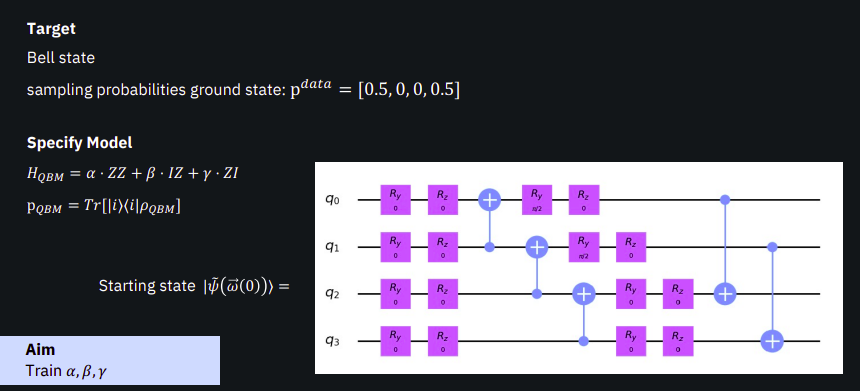
这篇文章描述了一个旨在获取贝尔状态采样概率知识的训练实例。它强调使用具有对角哈密顿量和有效 SE2 ansatz 的基本模型,该模型能够表示复杂的相。
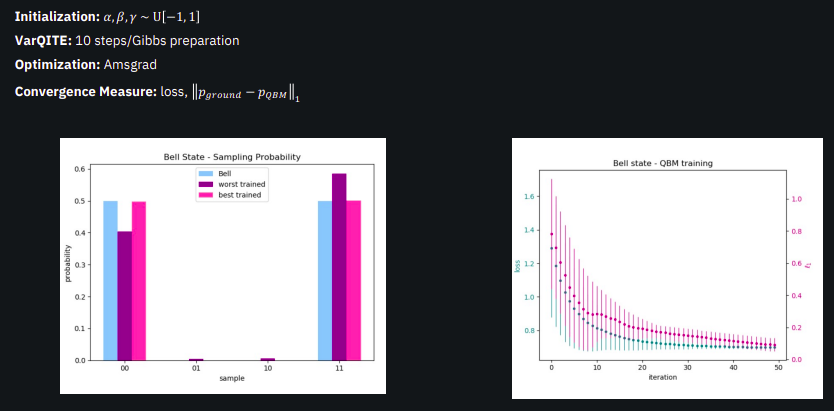
我们来分析一下训练结果。我们将参数(alpha、beta、gamma)初始化在 -1 到 1 的范围内。使用 VarQITE,我们通过 10 个步骤准备吉布斯状态并计算损失函数的梯度。这通过优化例程指导我们的模型训练。右侧显示损失函数的级数以及训练分布和期望分布之间的 L1 距离。每个图都附有标准差条,由 10 次不同随机状态运行的平均结果生成。值得注意的是,随着标准偏差的减小,我们看到了持续的改进。左侧的条形图说明了一个实例:蓝色条形是目标(贝尔状态采样),紫色条形代表最不有效的训练,粉红色条形是最好的。值得注意的是,即使是经过最好训练的结果也已经非常准确。
总之,变分量子玻尔兹曼机使我们能够有效地探索哈密顿量构造的数据结构,从而形成更加专注的状态学习器。利用自动微分,量子玻尔兹曼机训练变得容易进行,这得益于 VarQITE 用于吉布斯状态准备的固有用法。值得注意的是,由于其一致的电路深度和架构,该技术与近期的量子计算机非常吻合。
三、结论
总之,量子玻尔兹曼机代表了量子物理和机器学习十字路口的一个令人着迷且有前途的前沿领域。它对量子特性的利用引入了计算范式的转变,提供了彻底改变问题解决和数据分析的潜力。通过利用叠加和纠缠,QBM 并行处理信息的能力可能会在优化、模式识别和量子系统模拟等领域带来突破。尽管面临着新兴技术的典型挑战,包括纠错和降噪,但 QBM 的发展有可能重新定义计算的边界,为科学、技术和人工智能的新可能性打开大门。随着研究人员和工程师不断提升其能力,量子玻尔兹曼机最终可能会重新定义我们对计算的理解,并推动我们进入量子增强智能的新时代。



![[Linux] yum仓库相关](https://img-blog.csdnimg.cn/5fec5ae215b34c66bb98b7ce55deb9e2.png)




![半平面求交 - 洛谷 - P3256 [JLOI2013] 赛车](https://img-blog.csdnimg.cn/2020121310235323.png#pic_center)