一、说明
实验设计在科学研究中发挥着至关重要的作用,使研究人员能够从数据中得出有意义的结论。一种常见的实验设计是完全随机设计(CRD),其特征是将实验单元随机分配到治疗组。CRD 的方差分析 (ANOVA) 是一种统计技术,用于确定治疗组之间是否存在统计显着差异。在本文中,我们将探讨 CRD 方差分析的基本原理、其假设及其在现实世界研究中的应用。

完全随机设计的方差分析:科学与随机性相遇,揭示显着性模式。
二、完全随机设计:简要概述
完全随机设计是一种基本的实验设计,当研究人员有兴趣比较多个治疗或组时特别有用。在 CRD 中,实验单位被随机分配到不同的治疗组。这种随机化有助于消除偏差,并确保估计的治疗效果是无偏差的,并且可以推广到抽取样本的人群。
CRD 的关键组件包括:
- 治疗组:这些是正在测试的自变量的各个水平。每个组接受不同的治疗或条件。
- 随机分配:将实验单元随机分配到治疗组的过程,以确保每个单元有平等的机会被分配到任何组。
- 响应变量:为评估治疗效果而测量或观察的变量。
三、CRD 的方差分析
方差分析是一种统计方法,用于确定两个或多个组的平均值是否彼此显着不同。CRD 的方差分析专门解决了治疗组平均值之间是否存在显着差异的问题。该技术将数据的总变异分为两个部分:治疗组之间的变异和治疗组内的变异。
在数学上,CRD 的 ANOVA 模型可以表示为:
Yij = μ + τi + εij
其中:
- Yij 代表第 i 个治疗组中第 j 个个体的观察结果。
- μ 是总体平均值。
- τi 是第 i 个治疗组的效果。
- εij 是与第 i 个治疗组中第 j 个观察值相关的随机误差。
四、CRD 方差分析的假设
为了确保方差分析结果的有效性,必须满足几个假设:
- 独立性:治疗组内和治疗组之间的观察必须彼此独立。
- 正态性:残差的分布(观测值与预测值之间的差异)应近似正态分布。
- 方差同质性:所有治疗组的残差方差应保持恒定,这意味着每组内的变异性应大致相等。
- 随机分配:实验单位必须被随机分配到治疗组。
五、方差分析在 CRD 中的应用
CRD 方差分析广泛应用于各个科学研究领域,包括生物学、心理学、农业和制造业。让我们考虑一些实际的例子:
- 农业:研究人员可以使用 CRD 方差分析来比较不同肥料对作物产量的影响,以确定哪种肥料可使作物产量最高。
- 医学:临床试验经常使用 CRD 方差分析来评估不同药物治疗对特定病症的有效性。
- 心理学:心理学家可以采用 CRD 方差分析来研究各种疗法对患者心理健康结果的影响。
- 制造:质量控制工程师可以使用 CRD ANOVA 来评估不同制造工艺对产品质量的影响。
六、代码
下面是一个完整的 Python 代码示例,用于使用数据集执行完全随机设计 (CRD) 的方差分析 (ANOVA) 并生成相关图。为此,我们将使用scipy和库。matplotlib
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
# Sample dataset for three treatment groups (you can replace this with your own data)
data = {
'Group1': [82, 85, 88, 90, 92],
'Group2': [75, 78, 82, 86, 88],
'Group3': [72, 74, 76, 78, 80]
}
# Create a pandas DataFrame from the dataset
df = pd.DataFrame(data)
# Perform one-way ANOVA
f_statistic, p_value = stats.f_oneway(df['Group1'], df['Group2'], df['Group3'])
# Output ANOVA results
print("F-statistic:", f_statistic)
print("p-value:", p_value)
# Determine whether the differences are statistically significant
alpha = 0.05
if p_value < alpha:
print("The differences are statistically significant (reject the null hypothesis).")
else:
print("The differences are not statistically significant (fail to reject the null hypothesis).")
# Plot the data
plt.figure(figsize=(8, 6))
plt.boxplot([df['Group1'], df['Group2'], df['Group3']], labels=['Group 1', 'Group 2', 'Group 3'])
plt.title('Boxplot of Treatment Groups')
plt.xlabel('Treatment Groups')
plt.ylabel('Values')
plt.show()在此代码中,我们首先定义一个包含三个治疗组(Group1、Group2 和 Group3)的样本数据集。您可以将此数据替换为您自己的数据集。然后我们根据这个数据集创建一个 pandas DataFrame。
F-statistic: 8.861818181818181
p-value: 0.004329879787661512
The differences are statistically significant (reject the null hypothesis). 该代码继续执行单向方差分析,用于scipy.stats.f_oneway获取 F 统计量和 p 值。根据 p 值,它确定治疗组之间的差异在指定的显着性水平 (alpha) 下是否具有统计显着性。
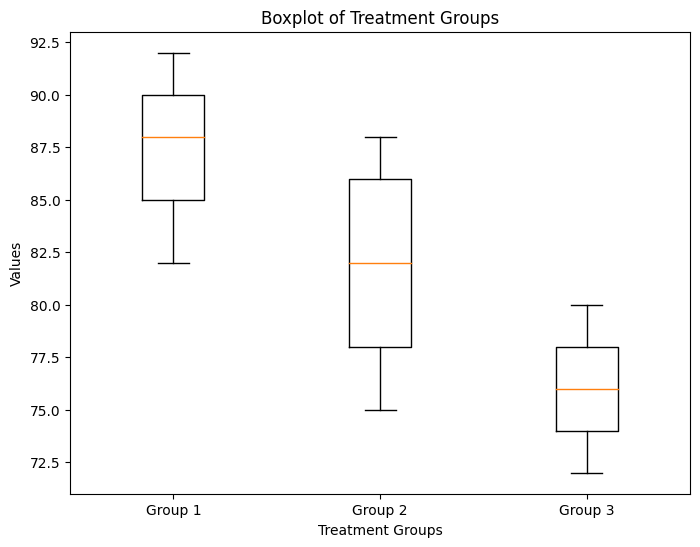
最后,代码生成一个箱线图来可视化每个治疗组中值的分布。
确保在您的 Python 环境中安装了pandas、scipy和库才能成功运行此代码。matplotlib
七、结论
完全随机设计的方差分析是一种强大的统计工具,使研究人员能够评估随机实验中治疗组之间差异的显着性。通过将数据的变化划分为组内和组间成分,方差分析可以帮助研究人员就不同治疗或条件的影响得出有意义的结论。必须确保满足独立性、正态性、方差同质性和随机分配的假设,以获得准确可靠的结果。CRD 方差分析仍然是科学研究的基石,有助于我们理解不同领域的各种现象。