1. 概念简述
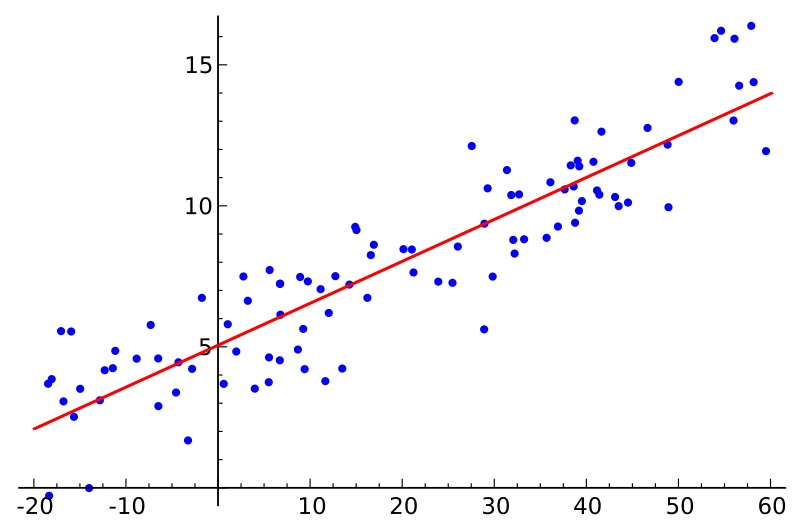
线性回归是通过一个或多个自变量与因变量之间进行建模的回归分析,其特点为一个或多个称为回归系数的模型参数的线性组合。如下图所示,样本点为历史数据,回归曲线要能最贴切的模拟样本点的趋势,将误差降到最小。
2. 线性回归方程
线形回归方程,就是有 n 个特征,然后每个特征 Xi 都有相应的系数 Wi ,并且在所有特征值为0的情况下,目标值有一个默认值 W0 ,因此:
线性回归方程为:
整合后的公式为:
3. 损失函数
损失函数是一个贯穿整个机器学习的一个重要概念,大部分机器学习算法都有误差,我们需要通过显性的公式来描述这个误差,并将这个误差优化到最小值。假设现在真实的值为 y,预测的值为 h 。
损失函数公式为:
也就是所有误差和的平方。损失函数值越小,说明误差越小,这个损失函数也称最小二乘法。
4. 损失函数推导过程
4.1 公式转换
首先我们有一个线性回归方程:
为了方便计算计算,我们将线性回归方程转换成两个矩阵相乘的形式,将原式的 后面乘一个
此时的 x0=1,因此将线性回归方程转变成 ,其中
和
可以写成矩阵:
4.2 误差公式
以上求得的只是一个预测的值,而不是真实的值,他们之间肯定会存在误差,因此会有以下公式:
我们需要找出真实值 与预测值
之间的最小误差
,使预测值和真实值的差距最小。将这个公式转换成寻找不同的
使误差达到最小。
4.3 转化为  求解
求解
由于 既存在正数也存在负数,所以可以简单的把这个数据集,看作是一个服从均值
,方差为
的正态分布。
所以  出现的概率满足概率密度函数:
出现的概率满足概率密度函数:
把 代入到以上的高斯分布函数(即正态分布)中,变成以下式子:
到此,我们将对误差 的求解转换成对
的求解了。
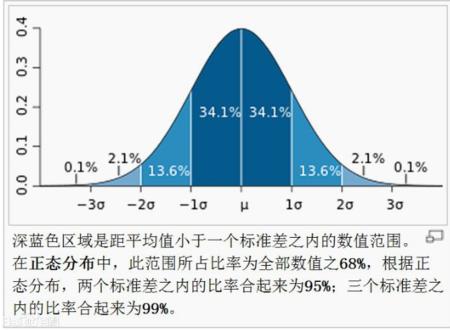
在求解这个公式时,我们要得到的是误差 最小,也就是求概率
最大的。因为误差
满足正态分布,因此在正太曲线中央高峰部的概率
是最大的,此时标准差
为0,误差是最小的。
尽管在生活中标准差肯定是不为0的,没关系,我们只需要去找到误差值出现的概率最大的点。现在,问题就变成了怎么去找误差出现概率最大的点,只要找到,那我们就能求出
4.4 似然函数求 
似然函数的主要作用是,在已经知道变量 x 的情况下,调整 ,使概率 y 的值最大。
似然函数理解:
以抛硬币为例,正常情况硬币出现正反面的概率都是0.5,假设你在不确定这枚硬币的材质、重量分布的情况下,需要判断其是否真的是均匀分布。在这里我们假设这枚硬币有 的概率会正面朝上,有
的概率会反面朝上。
为了获得 的值,将硬币抛10次,H为正面,T为反面,得到一个正反序列 x = HHTTHTHHHH,此次实验满足二项分布,这个序列出现的概率为
,我们根据一次简单的二项分布实验,得到了一个关于
的函数,这实际上是一个似然函数,根据不同的
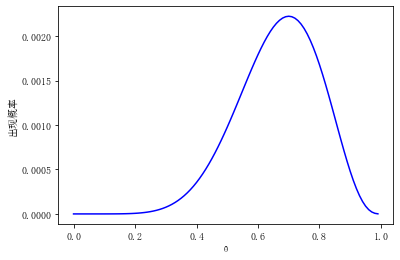
值绘制一条曲线,曲线就是
的似然函数,y轴是这一现象出现的概率。
从图中可见,当 等于 0.7 时,该序列出现的概率是最大的,因此我们确定该硬币正面朝上的概率是0.7。
因此,回到正题,我们要求的是误差出现概率 的最大值,那就做很多次实验,对误差出现概率累乘,得出似然函数,带入不同的
,看
是多少时,出现的概率是最大的,即可确定
的值。
综上,我们得出求  的似然函数为:
的似然函数为:
4.5 对数似然
由于上述的累乘的方法不太方便我们去求解 ,我们可以转换成对数似然,将以上公式放到对数中,然后就可以转换成一个加法运算。取对数以后会改变结果值,但不会改变结果的大小顺序。我们只关心
等于什么的时候,似然函数有最大值,不用管最大值是多少,即,不是求极值而是求极值点。注:此处log的底数为e。
对数似然公式如下:
对以上公式化简得:
4.6 损失函数
我们需要把上面那个式子求得最大值,然后再获取最大值时的 值。 而上式中
是一个常数项,所以我们只需要把减号后面那个式子变得最小就可以了,而减号后面那个部分,可以把常数项
去掉,因此我们得到最终的损失函数如下,现在只需要求损失函数的最小值。
注:保留 是为了后期求偏导数。
损失函数越小,说明预测值越接近真实值,这个损失函数也叫最小二乘法。
5. 梯度下降
损失函数中 xi 和 yi 都是给定的值,能调整的只有 ,如果随机的调整,数据量很大,会花费很长时间,每次调整都不清楚我调整的是高了还是低了。我们需要根据指定的路径去调节,每次调节一个,范围就减少一点,有目标有计划去调节。梯度下降相当于是去找到一条路径,让我们去调整
。
梯度下降的通俗理解就是,把对以上损失函数最小值的求解,比喻成梯子,然后不断地下降,直到找到最低的值。
5.1 批量梯度下降(BGD)
批量梯度下降,是在每次求解过程中,把所有数据都进行考察,因此损失函数因该要在原来的损失函数的基础之上加上一个m:数据量,来求平均值:
因为现在针对所有的数据做了一次损失函数的求解,比如我现在对100万条数据都做了损失函数的求解,数据量结果太大,除以数据量100万,求损失函数的平均值。
然后,我们需要去求一个点的方向,也就是去求它的斜率。对这个点求导数,就是它的斜率,因此我们只需要求出 的导数,就知道它要往哪个方向下降了。它的方向先对所有分支方向求导再找出它们的合方向。
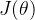 的导数为:
的导数为:
由于导数的方向是上升的,现在我们需要梯度下降,因此在上式前面加一个负号,就得到了下降方向,而下降是在当前点的基础上下降的。
批量梯度下降法下降后的点为:
新点是在原点的基础上往下走一点点,斜率表示梯度下降的方向, 表示要下降多少。由于不同点的斜率是不一样的,以此循环,找到最低点。
批量梯度下降的特点:每次向下走一点点都需要将所有的点拿来运算,如果数据量大非常耗时间。
5.2 随机梯度下降(SGD)
随机梯度下降是通过每个样本来迭代更新一次。对比批量梯度下降,迭代一次需要用到所有的样本,一次迭代不可能最优,如果迭代10次就需要遍历整个样本10次。SGD每次取一个点来计算下降方向。但是,随机梯度下降的噪音比批量梯度下降要多,使得随机梯度下降并不是每次迭代都向着整体最优化方向。
随机梯度下降法下降后的点为:
每次随机一个点计算,不需要把所有点拿来求平均值,梯度下降路径弯弯曲曲趋势不太好。
5.3 mini-batch 小批量梯度下降(MBGO)
我们从上面两个梯度下降方法中可以看出,他们各自有优缺点。小批量梯度下降法在这两种方法中取得了一个折衷,算法的训练过程比较快,而且也要保证最终参数训练的准确率。
假设现在有10万条数据,MBGO一次性拿几百几千条数据来计算,能保证大体方向上还是下降的。
小批量梯度下降法下降后的点为:
用来表示学习速率,即每次下降多少。已经求出斜率了,但是往下走多少合适呢,
值需要去调节,太大的话下降方向会偏离整体方向,太小会导致学习效率很慢。