🚀个人主页:为梦而生~ 关注我一起学习吧!
💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~
💡往期推荐:
【机器学习基础】机器学习入门(1)
【机器学习基础】机器学习入门(2)
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估(评估方法及性能度量原理及主要公式)
【机器学习基础】一元线性回归(适合初学者的保姆级文章)
💡本期内容:本篇文章紧接着上篇文章的回归模型,讲一下多元的线性回归~超级基础的文章,赶紧收藏学习吧!!!
文章目录
- 1 多元线性回归
- 1.1 什么是多元线性回归
- 1.2 多元的梯度下降
- 2 梯度下降需要注意的问题
- 2.1 学习率
- 2.2 特征缩放
- 2.3 特征与多项式回归
- 2.4 正规方程
1 多元线性回归
1.1 什么是多元线性回归
多元线性回归是一种统计分析方法,它涉及到两个或更多的自变量,并且因变量和自变量之间是线性关系。这种方法用于确定两个或更多个变量之间的定量关系。多元线性回归模型表示因变量(Y)与自变量(X1,X2,X3等)之间的线性关系。
- 承接我们上一篇文章预测房价的例子
目前为止,我们探讨了单变量线性回归模型,现在我们对房价模型增加更多的特征,例如房间的数量,楼层数和房屋的年龄等,构成一个含有多变量的模型,模型中的特征为(x1,x2,…,xn)。

增添更多特征后,看一下各个变量名:
-
n 代表特征的数量
-
x ( i ) x^{(i)} x(i)代表第i个训练实例,表示特征矩阵中的第i行,是一个向量,比如说,上图的
x ( 2 ) = ( 1416 3 2 40 232 ) x^{(2)}=\begin{pmatrix} 1416\\ 3\\ 2\\ 40\\ 232 \end{pmatrix} x(2)= 14163240232 -
x j ( i ) x_{j}^{(i)} xj(i)代表特征矩阵中第 𝑖 行的第 𝑗 个特征,也就是第 𝑖 个训练实例的第 𝑗 个特征。
假设函数:

这个公式中有n+1个参数和n个变量,为了能够使公式简化一些,引入
x
0
=
1
x_{0}=1
x0=1,则公式转化为:
h
θ
(
x
)
=
θ
0
x
0
+
θ
1
x
1
+
θ
2
x
2
+
.
.
.
+
θ
n
x
n
h_{\theta }(x)=\theta _{0}x_{0}+\theta _{1}x_{1}+\theta _{2}x_{2}+...+\theta _{n}x_{n}
hθ(x)=θ0x0+θ1x1+θ2x2+...+θnxn

与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,和单变量代价函数类似,这个代价函数也是所有建模误差的平方和,即

1.2 多元的梯度下降
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。
多变量线性回归的批量梯度下降算法为:

下面是一元与多元的区别:

2 梯度下降需要注意的问题
2.1 学习率
在梯度下降的公式中,𝑎是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向
向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。
- 学习率与偏导的共同作用:
α \alpha α 虽然决定了我们迈出的步子的大小,但是,步子的大小却不仅仅是由 α \alpha α 决定的,还与它后面的偏导数有关。 φ φ ϑ j J ( θ ) \frac{\varphi }{\varphi \vartheta _{j}}J(\theta ) φϑjφJ(θ)就是我们前面提到的“梯度”,梯度的本质是一个向量,(有大小,有方向),其大小和 α \alpha α 一同决定了迈出步子的大小,其方向决定了“下山”最快的方向。
- 学习率过大或者过小的影响:
- 学习率过小
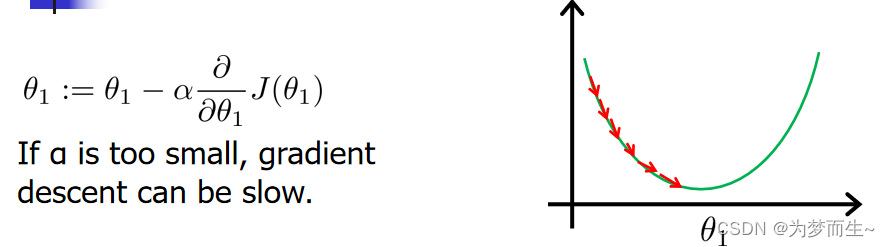
如果 α \alpha α太小,即我们下山的步子迈的很小,每次我们只能一点一点的移动,这样导致我们走的很慢,需要很多步才能走到最低点。
- 学习率过大
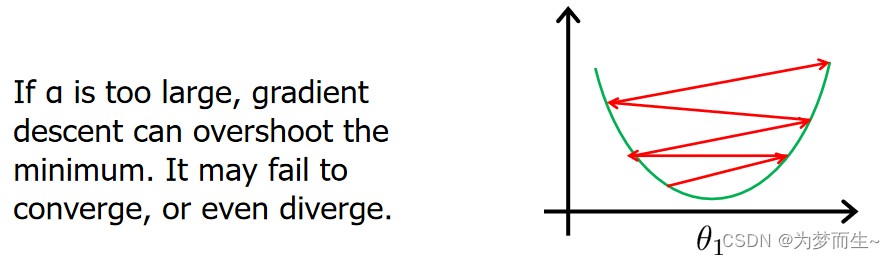
如果 α \alpha α太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛,下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来远。
2.2 特征缩放
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
来看下面这个例子:
假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0- 2000 平方英尺,而房间数量的值则是 0-5 ,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。

解决的方法是尝试将所有特征的尺度都尽量缩放到一个固定的范围内

我们只需要使用以下方法就可以做到这一点:


2.3 特征与多项式回归
对于这么多特征以及训练集,如何选择才会使得训练出来的函数预测效果更好呢?

如果需要更多的特征,我们的多项式会显得特别的冗长,我们可以将某些特征用另外的少数特征来代替,通过平方等方式表示:
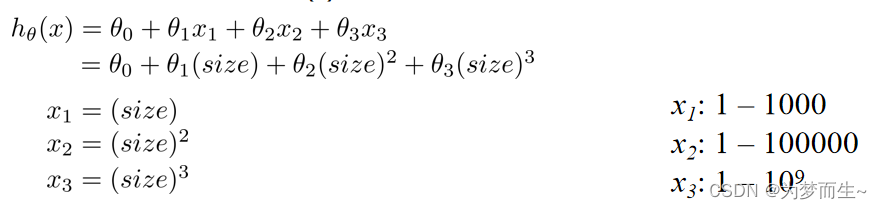
同时,为了减小计算量,前面的特征缩放的工作是十分有必要的。
2.4 正规方程
多元线性回归的正规方程是通过矩阵形式来求解线性回归参数的方法。其目的是通过求解导数为0来得到参数的最小二乘估计值。简单来说,正规方程是通过数学方法快速计算出线性回归模型的最优解。

由前面我们知道代价函数:
J
(
θ
)
=
1
2
m
Σ
i
=
1
m
h
θ
(
(
x
(
i
)
)
−
y
i
)
2
J(\theta )=\frac{1}{2m}\Sigma _{i=1}^{m}h_{\theta }((x^{(i)})-y^{i})^{2}
J(θ)=2m1Σi=1mhθ((x(i))−yi)2,我们也可以把它改写成下面的形式

这里我们的目标仍然是求代价函数的最小值,使用下面的方法就可以求出:对于每一个
θ
\theta
θ,都让它对应的偏导等于0
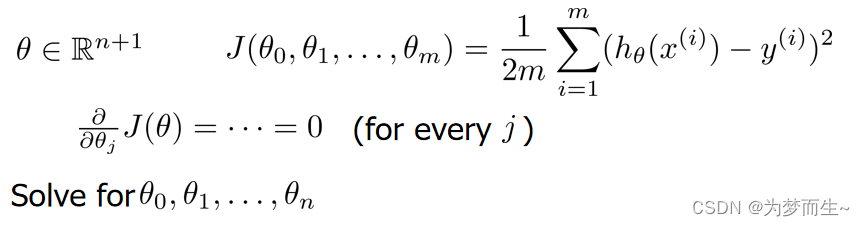
假设我们的训练集特征矩阵为 𝑋 (包含了 𝑥 0 = 1 )并且我们的训练集结果为向量 𝑦,则利用正规方程解出向量:
θ
=
(
X
T
X
)
−
1
X
T
y
\theta =(X^{T}X)^{-1}X^{T}y
θ=(XTX)−1XTy
下面是以四个特征为例,利用正规方程的求解:
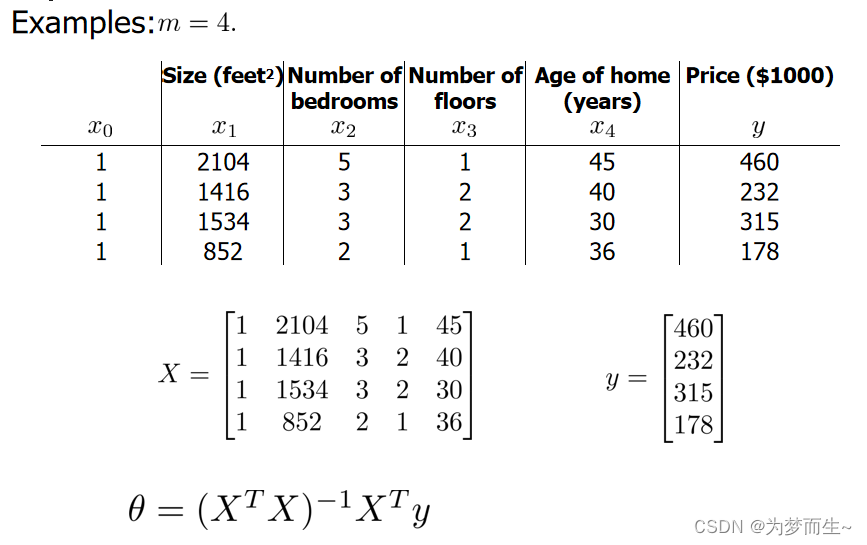
- 最后,这则方程和梯度下降法的比较:

- 另外:
梯度下降适用于各种模型,正则方程只适用于线性模型,不适用逻辑回归等其他模型