目录
1.X-bar 图的基本概念
2.X-bar 图的绘制过程
3.X-bar 图的优势
4.X-bar 图的绘制
1.X-bar 图的基本概念
X-bar控制图是一种统计工具,用于监控和控制生产过程中的质量变量。它是过程能力分析和统计过程控制(SPC,Statistical Process Control)的重要组成部分。X-bar控制图主要用于追踪过程平均值的变化,帮助识别过程是否处于受控状态。
X-bar控制图包括中心线(CL,Central Line),上限控制线(UCL,Upper Control Limit)和下限控制线(LCL,Lower Control Limit)。中心线通常是过程平均值的估计值,上限控制线和下限控制线是根据中心线和标准差计算得出的。
在X-bar控制图中,每个点表示一个样本的平均值。随着时间的推移,这些点应该会围绕中心线上下波动。如果点在控制限内,说明过程是受控的。如果点超出控制限,则说明过程可能失控,需要采取措施来调整和改进过程。
除了X-bar控制图外,还有其他类型的控制图,如均值-极差控制图(X-R图)和不合格品率控制图(P图)等。这些控制图都有各自的特点和用途,可以根据需要选择适合的控制图来监控生产过程的质量。
2.X-bar 图的绘制过程
收集数据:从生产过程中连续抽取样本,并记录每个样本的平均值。
计算平均值和范围:对每个样本计算平均值(X-bar)和范围(R)。
绘制图表:使用统计软件或手动绘制X-bar 图。图表上通常包括X-bar 和R 两个子图。
确定控制限:根据样本数据计算上限和下限,这有助于确定过程是否处于控制状态。
解读图表:监测X-bar 图以识别任何趋势、偏移或异常点。超出控制限的数据可能表明需要调整或改进生产过程。
3.X-bar 图的优势
实时监测:提供对生产过程实时性能的监控。
识别变异:有助于迅速识别过程中的变异,从而采取纠正措施。
持续改进: 通过识别问题,推动持续改进和质量管理。
4.X-bar 图的绘制
import numpy as np
import matplotlib.pyplot as plt
# 示例数据,包含10个子组的样本数据,每个子组有5个样本
data = np.array([
[10, 12, 11, 9, 17],
[14, 15, 13, 11, 12],
[10, 9, 11, 12, 10],
[12, 11, 10, 12, 11],
[9, 11, 22, 4, 12],
[11, 10, 15, 10, 11],
[13, 12, 11, 12, 14],
[10, 9, 11, 12, 10],
[12, 4, 34, 12, 11],
[9, 11, 10, 9, 12]
])
# 计算每个子组的平均值和范围
subgroup_Xmeans = np.mean(data, axis=1) # 计算每个子组的平均值
subgroup_Rranges = np.ptp(data, axis=1) # 计算每个子组的范围(即极差)
# 计算总体平均值
overall_Xmean = np.mean(subgroup_Xmeans) # 所有子组平均值的平均值,表示整体过程的中心位置。它是X-bar图中的中心线。
overall_Rmean = np.mean(subgroup_Rranges) # 所有子组的极差的平均值,表示整体过程的离散程度
# 计算A2、D3和D4常数(这里假设样本大小为5,您可以根据实际情况修改)
A2 = 0.577
D3 = 0
D4 = 2.114
# 计算控制限
UCL_X = overall_Xmean + A2 * overall_Rmean
LCL_X = overall_Xmean - A2 * overall_Rmean
UCLR = D4 * overall_Rmean
LCLR = D3 * overall_Rmean
# 计算R控制图的控制限(使用D4常数)
UCL_R = UCLR
LCL_R = LCLR
# 计算每个子组的Z分数
z_scores = (subgroup_Xmeans - overall_Xmean) / (overall_Rmean / np.sqrt(data.shape[1]))
# 设置阈值,通常选择2或3作为阈值
threshold = 3
# 异常检测并标记异常点
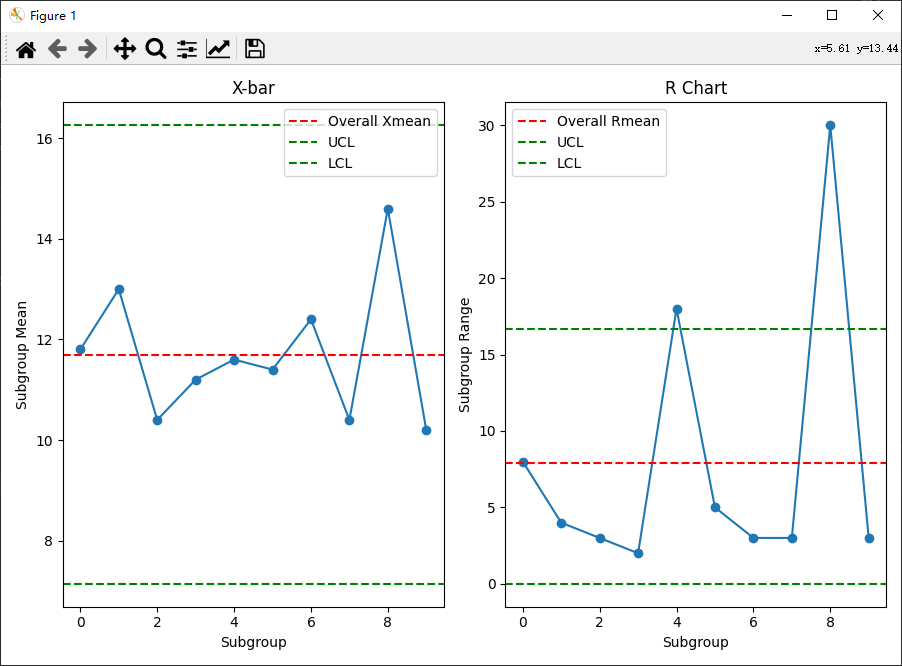
plt.figure(figsize=(9, 6))
plt.subplot(1, 2, 1)
plt.plot(subgroup_Xmeans, marker='o', linestyle='-')
plt.axhline(y=overall_Xmean, color='r', linestyle='--', label='Overall Xmean')
plt.axhline(y=UCL_X, color='g', linestyle='--', label='UCL')
plt.axhline(y=LCL_X, color='g', linestyle='--', label='LCL')
plt.legend()
plt.title('X-bar')
plt.xlabel('Subgroup')
plt.ylabel('Subgroup Mean')
# 异常检测 - 使用Z分数
outliers = np.where(np.abs(z_scores) > threshold)[0]
for o in outliers:
plt.annotate(f'Outlier (Subgroup {o + 1})', (o, subgroup_Xmeans[o]), textcoords="offset points", xytext=(0, 10),
ha='center')
# 绘制R控制图
plt.subplot(1, 2, 2)
plt.plot(subgroup_Rranges, marker='o', linestyle='-')
plt.axhline(y=overall_Rmean, color='r', linestyle='--', label='Overall Rmean')
plt.axhline(y=UCL_R, color='g', linestyle='--', label='UCL')
plt.axhline(y=LCL_R, color='g', linestyle='--', label='LCL')
plt.legend()
plt.title('R Chart')
plt.xlabel('Subgroup')
plt.ylabel('Subgroup Range')
plt.tight_layout()
plt.show()