文章目录
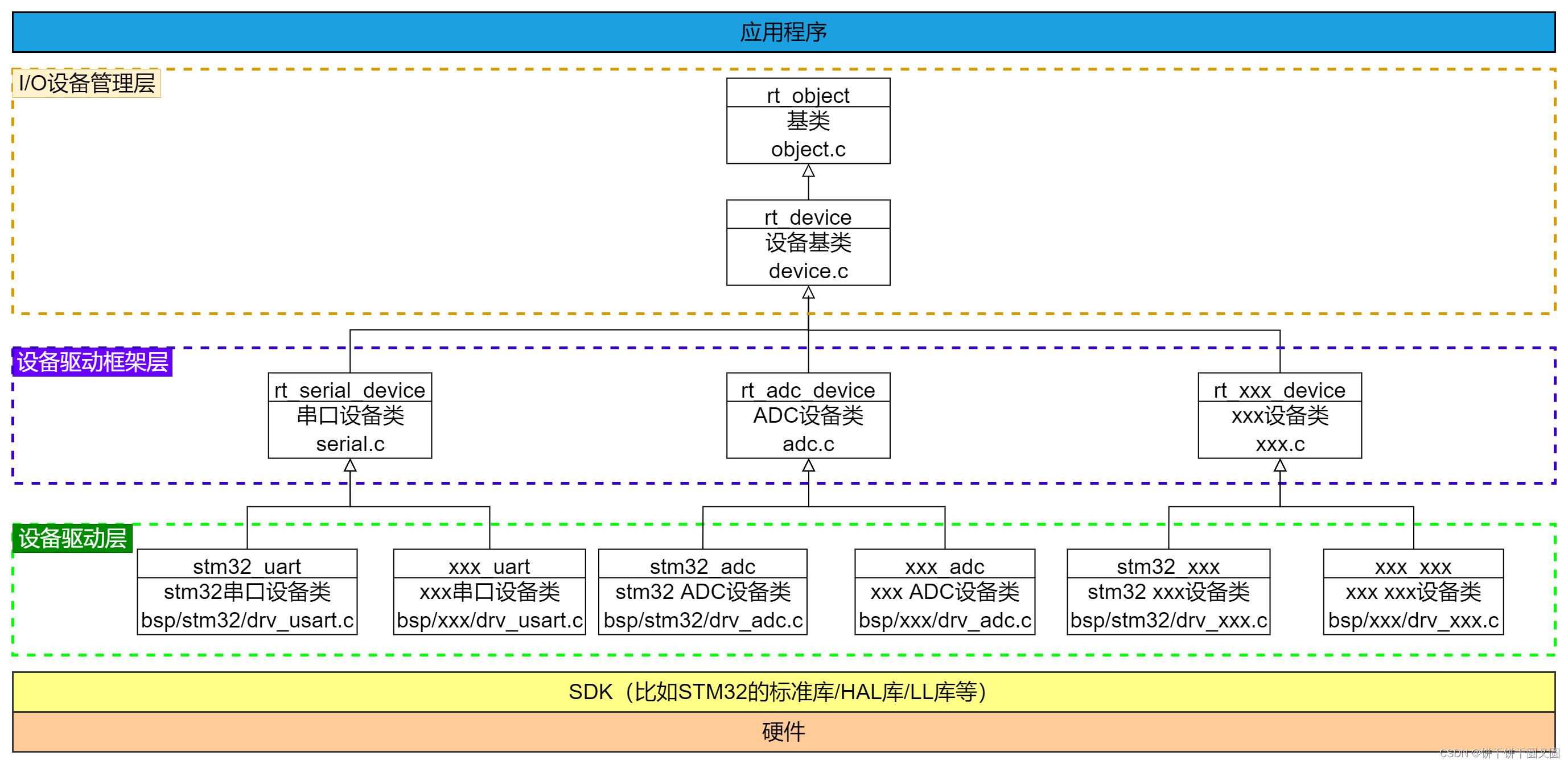
- 邻接矩阵
图的逻辑结构:多对多。
图没有顺序存储结构,但可以借助二维数组来表示元素间的关系。
数组表示法(邻接矩阵)。
多重链表:邻接表,邻接多重表,十字链表。
邻接矩阵(数组)表示法。
邻接表(链式)表示法。
1.数组(邻接矩阵)表示法
- 建立一个顶点表(记录各个顶点的信息)和一个邻接矩阵(表示各个顶点之间的关系)。
- 设图A=(V,E)有n个顶点,则

图的邻接矩阵是一个二维数组A.arcs[n][n],定义为:

无向图的邻接矩阵表示法
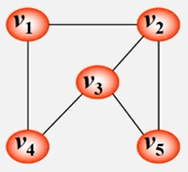
邻接矩阵A.arcs[i][j]:
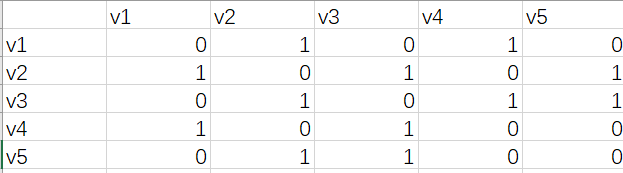
分析1:无向图的连接矩阵是对称的。
分析2:顶点i的度=第i行(列)中1的个数。
特别:完全图的邻接矩阵中,对角元素为0,其余为1。
有向图的邻接矩阵表示法
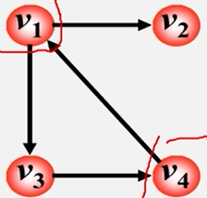
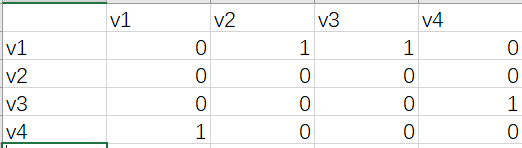
注:在有向图的邻接矩阵中,
第i行含义:以结点vi为尾的弧(即出度边);
第i列含义:以结点vi为头的弧(即入度边)。
分析1:有向图的邻接矩阵可能是不对称的。
分析2:顶点的出度=第i行元素之和。
顶点的入度=第i列元素之和。
网(即有权图)的邻接矩阵表示法
定义为:A.arcs[i][j]=Wij(有边或弧),∞(无边或弧)。
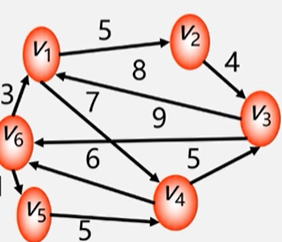
有向网的邻接矩阵:
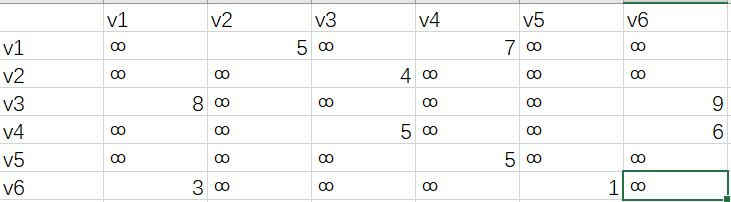
邻接矩阵
1.邻接矩阵的存储表示:用两个数组分别存储顶点表和邻接矩阵。
#define MaxInt 32767;//表示极大值,即无穷大
#define MVNum 100 //最大顶点数
typedef char VerTexType;//设顶点的数据类型为字符型
typedef int ArcType;//假设边的权值类型为整型
typedef struct {
VerTexType vexs[MVNum];//顶点表
ArcType arcs[MVNum][MVNum];//邻接矩阵
int vexnum, arcnum;//图的当前点数和边数
}AMGraph;
2.采用邻接矩阵表示法创建无向图。
【算法思想】
(1)输入总顶点和总边数。
(2)依次输入点的信息存入顶点表中。
(3)初始化邻接矩阵,使每个权值初始化为极大值。
(4)构造邻接矩阵。
#define MaxInt 32767;//表示极大值,即无穷大
#define MVNum 100 //最大顶点数
typedef char VerTexType;//设顶点的数据类型为字符型
typedef int ArcType;//假设边的权值类型为整型
typedef struct {
VerTexType vexs[MVNum];//顶点表
ArcType arcs[MVNum][MVNum];//邻接矩阵
int vexnum, arcnum;//图的当前点数和边数
}AMGraph;
//采用邻接矩阵表示创建无向表
int CreateUDN(AMGraph& G) {
int v1, v2,w;
int i,j,k;
cin >> G.vexnum >> G.arcnum;//输入总顶点数,总边数
for (i = 0; i < G.vexnum; ++i) {
cin >> G.vexs[i];//依次输入点的信息
}
for (i = 0; i < G.vexnum; ++i) {//初始化邻接矩阵
for (j = 0; j < G.vexnum; ++j) {
G.arcs[i][j] = MaxInt;//边的权值均置为极大值
}
}
for (k = 0; k < G.arcnum; ++k) {
//构造邻接矩阵
cin >> v1 >> v2 >> w;//输入一条边依附的顶点和权值
i = LocateVex(G, v1);
j = LocateVex(G, v2);//确定v1,v2在G中的位置,即顶点数组的下标
G.arcs[i][j] = w;//边<v1,v2>的权值设为w
G.arcs[j][i] = G.arcs[i][j];
}
return 1;
}
int LocateVex(AMGraph G, VerTexType u) {
//在图G中查找顶点u,存在则返回顶点表中的下标;否则则返回-1.
int i;
for (i = 0; i < G.vexnum; ++i) {
if (u == G.vexs[i]) {
return i;
}
return -1;
}
}