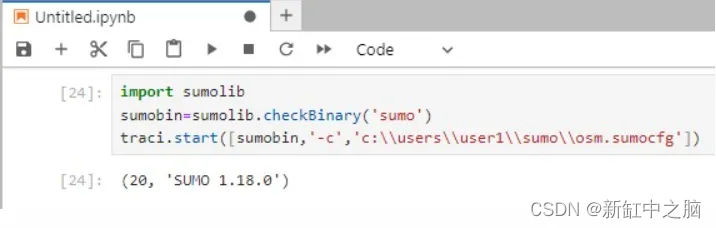
SARAS算法

news2024/11/23 23:55:19

SARAS算法

代码仓库:https://github.com/daiyizheng/DL/tree/master/09-rl

Sarsa算法是一种强化学习算法，用于解决马尔可夫决策过程（MDP）问题。它是一种基于值函数的方法，可以用于学习最优策略。本文将介绍Sarsa算法的流程。

SARSA算法流程

算法中各个参数的意义：

alpha是学习率, 来决定这次的误差有多少是要被学习的, alpha是一个小于1 的数.
gamma 是对未来 reward 的衰减值. 我们可以这样想象.
Q表示的是Q表格.
Epsilon greedy 是用在决策上的一种策略, 比如 epsilon = 0.9 时, 就说明有90% 的情况我会按照 Q 表的最优值选择行为, 10% 的时间使用随机选行为. 【这也是结合了强化学习中探索和利用的概念】

算法输入：迭代轮数 $T$ ，状态集 $S$ , 动作集 $A$ , 步长 $\alpha$ ，衰减因子 $\gamma$ , 探索率 $\epsilon$ ,
输出：所有的状态和动作对应的价值 $Q$

随机初始化所有的状态和动作对应的价值 $Q$ . 对于终止状态其 $Q$ 值初始化为0.
for i from 1 to T，进行迭代。
a) 初始化S为当前状态序列的第一个状态。设置 $A$ 为 $\epsilon-$ 贪婪法在当前状态 $S$ 选择的动作。
b) 在状态 $S$ 执行当前动作 $A$ ,得到新状态 $S^{'}$ 和奖励 $R$
c) 用 $\epsilon-$ 贪婪法在状态 $S^{'}$ 选择新的动作 $A^{'}$
d) 更新价值函数 $Q (S, A)$ : $\alpha(R+\gamma Q(S',A') - Q(S,A))$
e) $S = S^{'}, A = A^{'}$
f) 如果 $S^{'}$ 是终止状态，当前轮迭代完毕，否则转到步骤b)

这里有一个要注意的是，步长 $\alpha$ 一般需要随着迭代的进行逐渐变小，这样才能保证动作价值函数 $Q$ 可以收敛。当 $Q$ 收敛时，我们的策略 $\epsilon-$ 贪婪法也就收敛了。

与SARSA相比，Q-learning具有以下优点和缺点：

其实两种算法区别就在于对下一个状态的动作价值的估计，Q学习基于目标策略选定的动作，估计了一个价值，但是行为策略并不一定会真的选取执行这个动作。而SARSA则说，我自己选取的动作，我就是死也要执行。从“对下一个状态的评估”这个角度来说，SARSA更加谨慎，因为他基于他当前的策略选择最好的动作来执行，而QLearning则更大胆一点，下一个动作不一定就是目标策略的最优动作，甚至可能是随表挑的动作。

Q-learning直接学习最优策略，而SARSA在探索时学会了近乎最优的策略。
Q-learning具有比SARSA更高的每样本方差，并且可能因此产生收敛问题。当通过Q-learning训练神经网络时，这会成为一个问题。
SARSA在接近收敛时，允许对探索性的行动进行可能的惩罚，而Q-learning会直接忽略，这使得SARSA算法更加保守。如果存在接近最佳路径的大量负面报酬的风险，Q-learning将倾向于在探索时触发奖励，而SARSA将倾向于避免危险的最佳路径并且仅在探索参数减少时慢慢学会使用它。

注意： Q学习的区别只在于target的计算方法不同
SARSA的target计算公式:
target = Q(next_state,next_action) * gamma + reward
Q学习的target计算公式:
target = max(Q(next_state)) * gamma + reward

代码

环境

import gym


#定义环境
class MyWrapper(gym.Wrapper):

    def __init__(self):
        #is_slippery控制会不会滑
        env = gym.make('FrozenLake-v1',
                       render_mode='rgb_array',
                       is_slippery=False)

        super().__init__(env)
        self.env = env

    def reset(self):
        state, _ = self.env.reset()
        return state

    def step(self, action):
        state, reward, terminated, truncated, info = self.env.step(action)
        over = terminated or truncated

        #走一步扣一份,逼迫机器人尽快结束游戏
        if not over:
            reward = -1

        #掉坑扣100分
        if over and reward == 0:
            reward = -100

        return state, reward, over

    #打印游戏图像
    def show(self):
        from matplotlib import pyplot as plt
        plt.figure(figsize=(3, 3))
        plt.imshow(self.env.render())
        plt.show()


env = MyWrapper()

env.reset()

env.show()

Q动作价值函数

import numpy as np

#初始化Q表,定义了每个状态下每个动作的价值
Q = np.zeros((16, 4))

Q

单挑轨迹数据

from IPython import display
import random


#玩一局游戏并记录数据
def play(show=False):
    data = []
    reward_sum = 0

    state = env.reset()
    over = False
    while not over:
        action = Q[state].argmax()
        if random.random() < 0.1:
            action = env.action_space.sample()

        next_state, reward, over = env.step(action)

        data.append((state, action, reward, next_state, over))
        reward_sum += reward

        state = next_state

        if show:
            display.clear_output(wait=True)
            env.show()

    return data, reward_sum


play()[-1]

训练

#训练
def train():
    #共更新N轮数据
    for epoch in range(2000):

        #玩一局游戏并得到数据
        for (state, action, reward, next_state, over) in play()[0]:

            #Q矩阵当前估计的state下action的价值
            value = Q[state, action]

            #实际玩了之后得到的reward+(next_state,next_action)的价值*0.9
            target = reward + Q[next_state, Q[next_state].argmax()] * 0.9

            #value和target应该是相等的,说明Q矩阵的评估准确
            #如果有误差,则应该以target为准更新Q表,修正它的偏差
            #这就是TD误差,指评估值之间的偏差,以实际成分高的评估为准进行修正
            update = (target - value) * 0.02

            #更新Q表
            Q[state, action] += update

        if epoch % 100 == 0:
            print(epoch, play()[-1])


train()