数据结构和算法八股与手撕

news2024/11/25 1:05:37

数据结构和算法八股文

第一章 数据结构

1.1 常见结构

见http://t.csdnimg.cn/gmc3U

1.2 二叉树重点

1.2.1 各种树的定义

  • 满二叉树：只有度为0的结点和度为2的结点，并且度为0的结点在同一层上

  • 完全二叉树：除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。（优先级队列即堆是一棵完全二叉树）

    • 结点数为n的完全二叉树的叶子结点数量为n/2（n为偶数），(n+1)/2（n为奇数）
    • 通常使用数组存储完全二叉树，下标为i的结点的父结点下标为(i-1)/2，左孩子结点下标为2i+1，右孩子结点下标为2i+2

  • 二叉搜索树：有序树，若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉搜索树

  • 平衡二叉树：又称为AVL树，是一种特殊的二叉搜索树，它不仅满足了二叉搜索树的性质，而且左子树和右子树的高度之差的绝对值小于等于1；左子树和右子树也是平衡二叉树。其在插入和删除操作后，会通过自平衡的调整保持树的高度平衡，从而提高搜索、插入和删除等操作的效率。

    • C++中map、set、multiset、multimap底层都是红黑树（红黑树是平衡二叉树的一种特殊实现），增删查的时间复杂度为O(log n)。而unordered_set和unordered_map底层是哈希表，增删查的时间复杂度为O(1)；

  • 单支树：非叶子结点只有一个孩子节点，且方向一致

  • 哈夫曼树：压缩和解压缩用到的特殊二叉树是哈夫曼树，对应的方法是哈夫曼编码。（参考：https://blog.csdn.net/NOSaac/article/details/125901955）

    • 结点路径长度：两个节点中间隔线条数
    • 树的路径长度：除根结点外，其他结点到根结点路径长度之和
    • 结点带权路径长度：从该结点到根结点路径长度与结点上权的乘积
    • 树带权路径长度：树中所有叶子结点的带权路径长度之和
    • 构造方法：首先从权值列表中选择最小的两个结点，将其设置为左右（较小为左，较大为右）孩子结点，并设置其根节点的权值为两个权值之和，并将该结点加入到权值列表，删除权值列表中这两个最小结点。重复上述步骤，直至权值列表只有一个值后完成创建。
    • 哈夫曼树的带权路径长度最短。哈夫曼树没有度为1的结点，若有n个叶子结点则有n-1个非叶子结点，所有结点数目为2n-1。

1.2.2 使用ACM方式构建树

输入一行数据，第一个数字为结点总数，后面按层序遍历字符数组的方式输入结点，如果结点为空则输入#

#include <iostream>
#include <vector>
using namespace std;
struct TreeNode {
    char val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

int main() {
    int n;
    cin >> n;
    char c;
    vector<TreeNode*> vec(n);
    for (int i = 0; i < n; i++) {
        cin >> c;
        vec[i] = new TreeNode(c);
    }
    for (int i = 0; i < n; i++) {
        if (vec[i]->val == '#') continue;
        int leftIndex = 2 * i + 1, rightIndex = 2 * i + 2;
        if (leftIndex < n && vec[i]->val != '#') vec[i]->left = vec[leftIndex];
        else vec[i]->left = nullptr;
        if (rightIndex < n && vec[i]->val != '#') vec[i]->right = vec[rightIndex];
        else vec[i]->right = nullptr;
    }
    TreeNode* root = vec[0];  // root即为结果
    return 0;
}

1.2.3 二叉树遍历

  • 深度优先遍历：先往深走，遇到叶子结点再往回走。有前序遍历、中序遍历、后序遍历的递归法和迭代法实现（6个，其中中序遍历的迭代方法需要特殊记忆），中间结点的顺序即为遍历方式（前序遍历：中左右，中序遍历：左中右，后续遍历：左右中）
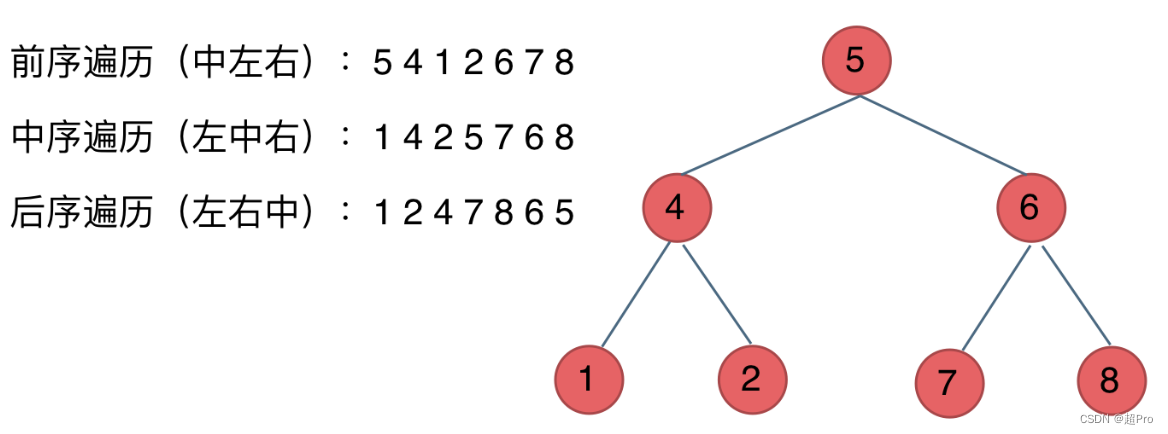
    在这里插入图片描述

  • 广度优先遍历：有层序遍历，通过迭代法实现（1个，需要特殊记忆）

1.2.3.1 前序遍历递归法实现

144. 二叉树的前序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector res;
    void traversal(TreeNode* root) {
        if (root == nullptr) return ;
        res.push_back(root->val);
        traversal(root->left);
        traversal(root->right);
    }
    vector preorderTraversal(TreeNode* root) {
        traversal(root);
        return res;
    }
};
1.2.3.2 前序遍历迭代法实现

144. 二叉树的前序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector preorderTraversal(TreeNode* root) {
        vector res;
        stack st;
        if (root != nullptr) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            res.push_back(node->val);
            if (node->right != nullptr) st.push(node->right);
            if (node->left != nullptr) st.push(node->left);
        }
        return res;
    }
};
1.2.3.3 中序遍历递归法实现

94. 二叉树的中序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector res;
    void traversal(TreeNode* root) {
        if (root == nullptr) return ;
        traversal(root->left);
        res.push_back(root->val);
        traversal(root->right);
    }
    vector inorderTraversal(TreeNode* root) {
        traversal(root);
        return res;
    }
};
1.2.3.4 中序遍历迭代法实现（着重记忆）

94. 二叉树的中序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector inorderTraversal(TreeNode* root) {
        vector res;
        stack st;
        TreeNode* node = root;
        while (node != nullptr || !st.empty()) {
            if (node != nullptr) {
                st.push(node);
                node = node->left;
            } else {
                node = st.top();
                st.pop();
                res.push_back(node->val);
                node = node->right;
            }
        }
        return res;
    }
};
1.2.3.5 后序遍历递归法实现

145. 二叉树的后序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector res;
    void traversal(TreeNode* root) {
        if (root == nullptr) return ;
        traversal(root->left);
        traversal(root->right);
        res.push_back(root->val);
    }
    vector postorderTraversal(TreeNode* root) {
        traversal(root);
        return res;
    }
};
1.2.3.6 后序遍历迭代法实现

145. 二叉树的后序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector postorderTraversal(TreeNode* root) {
        vector res;
        stack st;
        if (root != nullptr) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            res.push_back(node->val);
            if (node->left != nullptr) st.push(node->left);
            if (node->right != nullptr) st.push(node->right);
        }
        reverse(res.begin(), res.end());
        return res;
    }
};
1.2.3.7 层序遍历迭代法实现（着重记忆）

102. 二叉树的层序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> res;
        queue que;
        if (root != nullptr) que.push(root);
        while (!que.empty()) {
            vector vec;
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left != nullptr) que.push(node->left);
                if (node->right != nullptr) que.push(node->right);
            }
            res.push_back(vec);
        }
        return res;
    }
};

第二章 算法

2.1 时间复杂度

时间复杂度就是算法的时间度量，记为T(n)=O(f(n))，表示随着问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称为算法的渐进时间复杂度，简称时间复杂度。步骤：首先常数1取代加法常数，其次只保留最高阶项并把最高阶项的系数设为1。

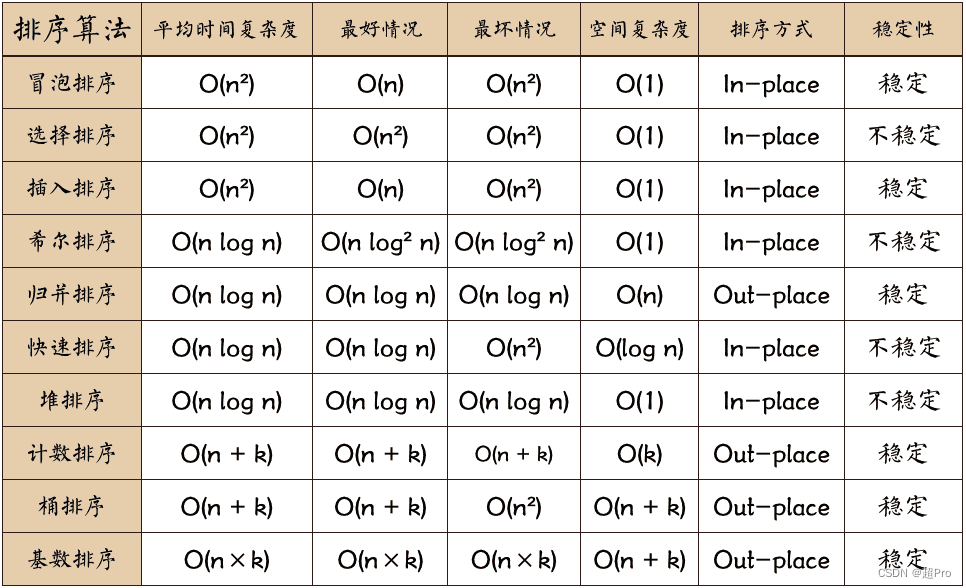
2.2 排序算法（重点）

  1. 冒泡排序：平均时间复杂度O(n2)、空间复杂度O(1)、稳定排序（相等元素位置不变）
  2. 选择排序：平均时间复杂度O(n2)、空间复杂度O(1)、非稳定排序
  3. 插入排序：平均时间复杂度O(n2)、空间复杂度O(1)、稳定排序
  4. 快速排序：平均时间复杂度O(nlog2n)、空间复杂度O(1)、非稳定排序
  5. 希尔排序：插入排序的优化版本。平均时间复杂度通常被认为是介于O(n)和O(n2)之间与增量序列有关，Hibbard 增量序列和 Knuth 增量序列等都可以使希尔排序达到 O(nlog2n) 的平均时间复杂度、空间复杂度O(1)、非稳定排序
  6. 归并排序：分治法，平均时间复杂度O(nlog2n)、空间复杂度O(n)、稳定排序
  7. 堆排序：时间复杂度O(nlog2n)、空间复杂度O(1)、非稳定排序
    在这里插入图片描述

2.2.1 冒泡排序

原理：重复地遍历待排序数组，每次比较相邻的两个元素，如果它们的顺序错误，就交换它们的位置，直到整个数组排序完成。

void bubbleSort(vector<int>& nums) {
    int n = nums.size();
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n - i - 1; j++) {
	    if (nums[j] > nums[j + 1]) swap(nums[j], nums[j + 1]);
        }
    }
}

2.2.2 选择排序

原理：将待排序的数组分成已排序和未排序两部分，每次从未排序部分选择最小的元素，然后与未排序部分的第一个元素交换，并将其放到已排序部分的末尾。重复这个过程直到整个数组排序完成。

void selectionSort(vector<int>& nums) {
    int n = nums.size();
    for (int i = 0; i < n; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (nums[j] < nums[minIndex]) minIndex = j;
        }
        swap(nums[i], nums[minIndex]);
    }
}

2.2.3 插入排序

原理：将待排序的数组分成已排序和未排序两部分，每次从未排序部分取出第一个元素，从后往前在已排序部分找到合适的位置插入该元素，直到所有元素都完成插入。

void insertSort(vector<int>& nums) {
    int n = nums.size();
    for (int i = 1; i < n; i++) {
        if (nums[i] < nums[i - 1]) {
            int temp = nums[i];
            int j = i - 1;
            while (j >= 0 && nums[j] > temp) {
                nums[j + 1] = nums[j];
                j--;
            }
            nums[j + 1] = temp;
        }
    }
}

2.3.4 快速排序

图解参考：https://blog.csdn.net/king13059595870/article/details/103421774

原理：分治法+双指针：选择第一个元素为基准，然后将数组分割为两个子数组，左边的子数组中的元素都比基准小，右边的子数组中的元素都比基准大。然后对两个子数组进行递归排序，直到整个数组完成排序。

void fastSort(vector<int>& nums, int low, int high) {
    if (low >= high) return;
    int first = low;
    int last = high;
    int key = nums[first];  // 选择首元素作为中轴元素（即基准）
    while (first < last) {
        // 从右往左，将比第一个小的移到前面
        while (first < last && nums[last] > key) last--;
        if (first < last) nums[first++] = nums[last];

        // 从左往右，将比第一个大的移到后面
        while (first < last && nums[first] < key) first++;
        if (first < last) nums[last--] = nums[first];
    }
    nums[first] = key;
    fastSort(nums, low, first - 1);
    fastSort(nums, first + 1, high);
}

2.3.5 希尔排序

代码参考：https://blog.csdn.net/weixin_44915226/article/details/119512633

原理：希尔排序是插入排序的一种，通过逐步缩小间隔来分组进行插入排序，从而提高排序的效率。

void shellSort(vector<int>& nums) {
    int n = nums.size();
    for (int gap = n / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < n; i++) {
	    if (nums[i] < nums[i - gap]) {
	        int temp = nums[i];
                int j = i - gap;
                while (j >= 0 && nums[j] > temp) {
                    nums[j + gap] = nums[j];
                    j -= gap;
                }
                nums[j + gap] = temp;
	    }
        }
    }
}

2.3.6 归并排序

图解参考：https://blog.csdn.net/qq_38307826/article/details/107445750

原理：分治法

  1. 先分解：将待排序的数组不断地二分，直到每个子数组都只包含一个元素，即认为它们已经排好序。
  2. 再合并：将两个有序的子数组合并为一个有序数组，在合并的过程中保持元素有序性。

归并排序使用了递归的方式来分解和合并，最终得到一个完全有序的数组。

void mergeSort(vector<int>& nums, vector<int>& numsTemp, int low, int high) {
    if (low >= high) return ;
    int mid = low + (high - low) / 2;
    int first1 = low, last1 = mid;
    int first2 = mid + 1, last2 = high;
    mergeSort(nums, numsTemp, start1, end1);
    mergeSort(nums, numsTemp, start2, end2);
    int index = low;
    while (first1 <= last1 && first2 <= last2) numsTemp[index++] = nums[first1] < nums[first2] ? nums[first1++] : nums[first2++];
    while (first1 <= last1) numsTemp[index++] = nums[first1++];
    while (first1 <= last1) numsTemp[index++] = nums[first2++];
    for (index = low; index <= high; index++) nums[index] = numsTemp[index];
}

2.3.7 堆排序

原理：堆排序是一种基于堆的排序算法，通过构建大顶堆并反复将堆顶元素与数组末尾交换，实现将最大值置于末尾，然后逐步递减堆的规模得到有序数组。

  • 堆是一棵完全二叉树，分为大顶堆和小顶堆，大顶堆指父节点数值大于等于左右孩子结点数值，小顶堆指父节点数值小于等于左右孩子结点数值。
  • 通常使用数组存储完全二叉树，下标为i的结点的父结点下标为(i-1)/2，左孩子结点下标为2*i+1，右孩子结点下标为2*i+2。
void heapify(vector<int>& nums, int n, int root) {
    int largest = root;
    int left = 2 * root + 1;
    int right = 2 * root + 2;
    if (left < n && nums[largest] < nums[left]) largest = left;
    if (right < n && nums[largest] < nums[right]) largest = right;
    if (largest != root) {
	swap(nums[root], nums[largest]);
	heapify(nums, n, largest);
    }
}
void heapSort(vector<int>& nums) {
    int n = nums.size();
    for (int i = n / 2 - 1; i >= 0; i--) heapify(nums, n, i);
    for (int i = n - 1; i >= 0; i++) {
	swap(nums[0], nums[i]);
	heapify(nums, i, 0);
    }
}

第三章 常见手撕

3.1 反转链表

206. 反转链表

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* cur = head;
        ListNode* pre = nullptr;
        while (cur) {
            // 逻辑顺序：先保存cur->next（temp），再将cur->next指向pre，pre指向cur，cur指向temp
            ListNode* temp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }
};

3.2 字母异位分组

49. 字母异位词分组

#include 
#include 
#include 
#include 
#include 

using namespace std;

int main() {
    vector strs= {"eat", "aet", "tea", "ban"};
    vector> res;
    unordered_map> umap;
    for (auto s : strs) {
        string skey = s;
        sort(skey.begin(), skey.end());
        umap[skey].push_back(s);
    }
    for (auto i : umap) res.push_back(i.second);

    // 输出结果
    for (auto r : res) {
        cout << "[";
        for (int i = 0; i < group.size(); i++) {
            cout << r[i];
            if (i < r.size() - 1) {
                cout << ", ";
            }
        }
        cout << "]," << endl;
    }
    return 0;
}

3.3 验证二叉搜索树

中序遍历构造数组，之后判断数组是否升序

98. 验证二叉搜索树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector vec;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val);
        traversal(root->right);
    }
    bool isValidBST(TreeNode* root) {
        traversal(root);
        for (int i = 0; i < vec.size() - 1; i++) {
            if (vec[i] >= vec[i + 1]) return false;
        }
        return true;
    }
};

3.4 粉刷房子II

力扣256

假如有一排 n 个房子，每个房子可以被粉刷成 k 种颜色中的一种，你需要粉刷所有的房子，使得相邻的房子不能够有相同的颜色。

费用函数 cost[i][j] 表示粉刷第 i 个房子使用颜色 j 的费用。

你需要找到所有房子粉刷完所需的最小费用。

注意：所有花费都是正整数。

#include 
#include 
#include   // climits包括INT_MAX，INT_MIN等宏
using namespace std;

int minCostII(vector>& costs) {
    if (costs.empty() || costs[0].empty()) return 0;

    int n = costs.size();
    int k = costs[0].size();
    
    // 1. 明确dp数组的下标及含义：dp[i][j]表示粉刷前i个房子，且最后一个房子使用颜色j粉刷的最小成本
    vector> dp(n, vector(k, 0));
    
    // 2. dp数组初始化，第0个房子粉刷颜色j的最小成本（即为costs[0][j]）
    for (int j = 0; j < k; ++j) dp[0][j] = costs[0][j];
    
    // 3. 确定递推公式：对于每个颜色 j，找到上一个房子的最小成本，但不能是同颜色，因此需要遍历上一个房子的所有颜色，取除了 j 颜色之外的最小成本。
    // 4. 确定遍历顺序：由左到右
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < k; j++) {
            int min_cost = INT_MAX;
            for (int m = 0; m < k; m++) {
                if (m != j) min_cost = min(min_cost, dp[i - 1][m]);
            }
            dp[i][j] = costs[i][j] + min_cost;
        }
    }
    
    // 最终，遍历最后一个房子的所有颜色 j，找出最小的成本作为结果。
    int result = INT_MAX;
    for (int j = 0; j < k; ++j) result = min(result, dp[n - 1][j]);

    return result;
}

int main() {
    vector> costs = {{1, 5, 3}, {2, 9, 4}};
    int result = minCostII(costs);
    cout << "Minimum cost: " << result << endl;
    
    return 0;
}

3.5 16进制转为10进制

#include 
using namespace std;
int stoi(char* s) {
    int res = 0;
    while (*s != '\0') {
        if (*s >= '0' && *s <= '9') res = res * 16 + (*s - '0');
        else if (*s >= 'a' && *s <= 'f') res = res * 16 + (*s - 'a' + 10);
        else if (*s >= 'A' && *s <= 'F') res = res * 16 + (*s - 'A' + 10);
        else return 0; 
        s++;
    }
    return res;
}

int main() {
    char s[] = {"e567"};
    cout << stoi(s) << endl;;
}

3.6 LRU算法（高频）

146. LRU 缓存

思路：双向链表+哈希表

参考https://leetcode.cn/problems/lru-cache/solutions/863539/146-lru-huan-cun-ji-zhi-cxiang-xi-ti-jie-ulv8/

class LRUCache {
public:
    // 定义双向链表，每个结点有key、value值，且有指向左结点和右节点的指针，最近使用过的结点放在左侧，最久未使用放在右侧
    /* 使用双向链表的原因：如果使用单向链表，只能获取后继结点，不能获取前驱结点，删除结点时需要遍历找到前驱结点，时间复杂度为O(n)；而是用双向链表可以直接获得前驱结点
    */
    struct ListNode {
        int key;
        int value;
        ListNode* left;
        ListNode* right;
        ListNode(int k, int v) : key(k), value(v), left(nullptr), right(nullptr) {}
    };
    ListNode* L = new ListNode(-1, -1);  // 虚拟头结点
    ListNode* R = new ListNode(-1, -1);  // 虚拟尾结点
    int n;  // 存储容量大小
    LRUCache(int capacity) {
        // 初始时，虚拟头结点和尾结点相接
        L->right = R;
        R->left = L;
	n = capacity;
    }

    // 定义哈希表，key为链表结点中的key，value为链表结点
    unordered_map umap;

    // 删除双向链表中的某个结点
    void remove(ListNode* node) {
        node->left->right = node->right;
        node->right->left = node->left;
    }
    
    // 在双向链表进行头插结点（最近使用的放在左侧，即链表头）
    void insert(ListNode* node) {
        node->right = L->right;
        node->left = L;
        L->right->left = node;
        L->right = node;
    }

    // 如果在哈希表中找不到key则返回-1。如果找到key的话，将对应的结点移动到链表头（先删再插）
    int get(int key) {
        if (umap.find(key) == umap.end()) return -1;
        ListNode* node = umap[key];
        remove(node);
        insert(node);
        return node->value;
    }
    
    // 如果要put的key在哈希表中，则更新哈希表中该结点value，将对应的结点移动到链表头（先删再插）；如果不在哈希表中且缓存已满，先删除链表中最后一个结点和哈希表中该值，再构建新的结点，并插入链表头和哈希表
    void put(int key, int value) {
        if (umap.find(key) != umap.end()) {
            ListNode* node = umap[key];
            node->value = value;
            remove(node);
            insert(node);
        } else {
            if (umap.size() == n) {
                ListNode* node = R->left;
                remove(node);
                umap.erase(node->key);
                delete node;
            }
            ListNode* node = new ListNode(key, value);
            insert(node);
            umap[key] = node;
        }
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

3.7 接雨水（高频）

42. 接雨水

思路：单调栈

计算方法：按行来计算雨水体积，使用单调栈，从栈顶到栈底的顺序应该是从小到大的顺序，因为如果将要添加的元素大于栈顶元素，则出现凹槽：栈顶元素是凹槽的底部柱子，栈顶的第二个元素是凹槽左侧柱子，要添加的元素是凹槽右侧柱子。由于通过宽*高来计算雨水的体积，既需要知道元素值，又需要知道元素的下标，因此单调栈中存储元素下标，元素值则通过下标来获得。

单调栈逻辑：

  • 当前遍历的元素小于栈顶元素：压入新元素的下标
  • 当前遍历的元素等于栈顶元素：弹出栈顶的下标，压入新元素的下标
  • 当前遍历的元素大于栈顶元素：计算栈顶元素雨水体积，弹出栈顶的下标，并压入新元素的下标
class Solution {
public:
    int trap(vector& height) {
        stack st;
        int res = 0;
        st.push(0);
        for (int i = 1; i < height.size(); i++) {
            if (height[i] < height[st.top()]) st.push(i);
            else if (height[i] == height[st.top()]) {
                st.pop();
                st.push(i);
            } else {
                while (!st.empty() && height[i] > height[st.top()]) {
                    int mid = st.top();
                    st.pop();
                    if (!st.empty()) {
                        int h = min(height[st.top()], height[i]) - height[mid];
                        int w = i - st.top() - 1;
                        res += h * w;
                    } 
                }
                st.push(i);
            }
        }
        return res;
    }
};

3.8 合并有序链表

剑指 Offer 25. 合并两个排序的链表

**迭代：**当list1和list2都不是空链表时，判断list1和list2哪一个链表的头节点的值更小，将较小值的节点添加到结果里，当一个节点被添加到结果里之后，将对应链表中的节点向后移一位。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* pre = dummyHead;
        while (list1 != nullptr && list2 != nullptr) {
            if (list1->val <= list2->val) {
                pre->next = list1;
                list1 = list1->next;
            } else {
                pre->next = list2;
                list2 = list2->next;
            }
            pre = pre->next;
        }
        pre->next = list1 == nullptr ? list2 : list1;
        return dummyHead->next;
    }
};

3.9 二进制求和

67. 二进制求和

class Solution {
public:
    string addBinary(string str1, string str2) {
        int n1 = str1.size();
        int n2 = str2.size();
        if (n1 < n2) {
            swap(str1, str2);
            swap(n1, n2);
        }
        
        while (n2 < n1) {
            str2 = '0' + str2;
            n2++;
        }

        for(int j = n1 - 1; j > 0; j--) {
            str1[j] = str1[j] - '0' + str2[j];
            if (str1[j] >= '2') {
                str1[j] = (str1[j] - '0') % 2 + '0';
                str1[j - 1] = str1[j - 1] + 1;
            }
        }
        str1[0] = str1[0] - '0' + str2[0];
        if(str1[0] >= '2') {
            str1[0] = (str1[0] - '0') % 2 + '0';
            str1 = '1' + str1;
        }
        return str1;
    }
};

3.10 实现strStr()

28. 找出字符串中第一个匹配项的下标

class Solution {
public:
    void getNext(int* next, string s) {
        int j = -1;
        next[0] = j;
        for (int i = 1; i < s.size(); i++) {
            while (j >= 0 && s[i] != s[j + 1]) j = next[j];
            if (s[i] == s[j + 1]) j++;
            next[i] = j;
        }
    }
    int strStr(string haystack, string needle) {
        int next[needle.size()];
        getNext(next, needle);
        int j = -1;
        for (int i = 0; i < haystack.size(); i++) {
            while (j >= 0 && haystack[i] != needle[j + 1]) j = next[j];
            if (haystack[i] == needle[j + 1]) j++;
            if (j == needle.size() - 1) return i - needle.size() + 1;
        }
        return -1;
    }
};

3.11 华为0913机试

https://mp.weixin.qq.com/s/BlpsEoitip7ugQYgezCd3g

3.11.1 快递中转站

快递公司有一个业务要求，所有当天下发到快递中转站的快递，最迟在第二天送达用户手中。

假设已经知道接下来n天每天下发到快递中转站的快递重量。快递中转站负责人需要使用快递运输车运输给用户，每一辆运输车最大只能装k重量的快递。

每天可以出车多次，也可以不出车，也不要求运输车装满。当天下发到快递中转站的快递，最晚留到第二天就要运输走送给用户。

快递中转站负责人希望出车次数最少，完成接下来n天的快递运输。

解答要求

时间限制: C/C++ 1000ms,其他语言: 2000ms内存限制: C/C++256MB其他语言: 512MB

输入

输入第一行包含两个整数n(1<= n<=200000)，k(1<=k<=100000000)

第二行包含n个整数ai，表示第i天下发到快递中转站的快递重量。

输出

输出最少需要的出车次数。

样例1

输入

3 2
3 2 1

输出

3

解释

第一天的快递出车一次送走2个重量，留1个重量到第二天

第二天送走第一天留下的1个重量和当前的1个重量，留1个重量到第三天送走。

解题思路：直接模拟

#include 
#include 
using namespace std;

int main() {
    int n, k;
    cin >> n >> k;
    vector vec(n);
    for (int i = 0; i < n; i++) cin >> vec[i];
    long long res = 0;
    long long left = 0;
    for (int i = 0; i < n; i++) {
        long long val = vec[i] + left;
        long long t1 = val / k;
        long long t2 = val % k;
        if (t1 == 0 && left != 0) {
            t1++;
            t2 = 0;
        }
        res += t1;
        left = t2;
    }
    if (left != 0) res++;
    cout << res << endl;
}

3.11.2 互通设备集

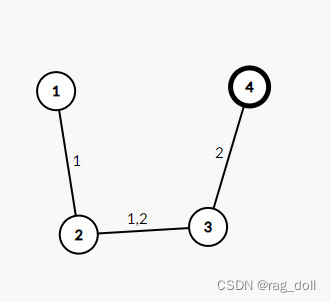
局一局域网内的设备可以相互发现，具备直连路由的两个设备可以互通。假定设备A和B互通，B和C互通，那么可以将B作为中心设备，通过多跳路由策略使设备A和C互通。这样，A、B、C三个设备就组成了一个互通设备集。其中，互通设备集包括以下几种情况:

  1. 直接互通的多个设备
  2. 通过多跳路由第略间接互通的多个设备
  3. 没有任何互通关系的单个设备现给出某一局域网内的设备总数以及具备直接互通关系的设备，请计算该局域网内的互通设备集有多少个?

输入

第一行: 某一局域网内的设备总数M，32位有符号整数表示。1<= M<=200

第二行:具备直接互通关系的数量N，32位有符号整数表示。0<= N<200

第三行到第N+2行: 每行两个有符号32位整数，分别表示具备直接互通关系的两个设备的编号，用空格隔开。每个设备具有唯一的编号，0<设备编号< M

输出

互通设备集的数量，32位有符号整数表示。

样例1

输入

3
2
0 1
0 2

输出

1

解释:

编号0和1以及编号0和2的设备直接互通，编号1和2的设备可通过编号0的设备建立互通关系，互通设备集可合并为1个。

#include 
#include 
#include 
using namespace std;

void dfs(int i, vector> connected, unordered_set& processed) {
    processed.insert(i);
    for (auto j : connected[i]) {
	if (processed.find(j) == processed.end()) dfs(j, connected, processed);
    }
}
int main() {
    int M, N;
    cin >> M >> N;
    vector> connected(M);
    for (int i = 0; i < N; i++) {
        int val1, val2;
        cin >> val1 >> val2;
	connected[val1].insert(val2);
        connected[val2].insert(val1);
    }
    int res = 0;
    unordered_set processed;
    for (int i = 0; i < M; i++) {
        if (processed.find(i) == processed.end()) {
            dfs(i, connected, processed);
            res++;
        }
    }
    cout << res << endl;
    
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1206820.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Looking for downloadable pre-built shared indexes关闭

Looking for downloadable pre-built shared indexes关闭

这个功能很烦,把他关闭就行了 PyCharm的“Looking for downloadable pre-built shared indexes”是指PyCharm IDE中的一个功能&#xff0c;用于搜索和下载可共享的预构建索引。 这个功能的主要用途是帮助开发人员在开发过程中快速地获取和使用预构建的索引&#xff0c;以提高…
阅读更多...
AtCoder ABC152

AtCoder ABC152

C - Low Elements 从前往后维护一个最长下降子序列 D - Handstand 2 设f[a][b]代表当前第一个数字为a第二个数字为b的数总个数 递推一下就可以。注意ab的情况。 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.py # software : PyCharmimport bi…
阅读更多...
打造全身视角的医院可视化能源监测管理平台，实现医院能源可视化管理

打造全身视角的医院可视化能源监测管理平台，实现医院能源可视化管理

医院是大型公共建筑的一种&#xff0c;随着医院规模的不断扩大&#xff0c;医院能源消耗剧增&#xff0c;能源消耗居高不下。医院对于能源监管的需求也越来越高。医院建立一套能耗监测管理平台&#xff0c;对于降低医院能耗有着非常重要的作用。 医院能耗存在的问题 1、医院能…
阅读更多...
如何挑选RPA开发商？

如何挑选RPA开发商？

其实&#xff0c;只要在这个行业调查的时间足够&#xff0c;不难发现里面有很多弯弯绕绕。 首先&#xff0c;RPA厂商虽然很多&#xff0c;但是优秀的RPA厂商就那么几家&#xff0c;它们都有各自擅长的领域&#xff0c;像金智维&#xff0c;就是在金融领域、政务领域&#xff1…
阅读更多...
释放潜能，加速创新 | 低代码赋能企业数据资产管理（附案例）

释放潜能，加速创新 | 低代码赋能企业数据资产管理（附案例）

在当今数字化快速发展的时代&#xff0c;企业要想保持竞争力&#xff0c;就必须紧跟潮流&#xff0c;不断进行自我革新。其中&#xff0c;数字化转型已成为企业发展的重要一环&#xff0c;在这个过程中&#xff0c;数据资产作为企业核心竞争力的关键组成部分&#xff0c;其管理…
阅读更多...
pytorch tensor数据类型转换为python数据

pytorch tensor数据类型转换为python数据

一、item() input: x torch.tensor([1.0]) x.item()output: 1.0二、tolist() input: a torch.randn(2, 2) a.tolist() a[0,0].tolist()output: [[0.012766935862600803, 0.5415473580360413],[-0.08909505605697632, 0.7729271650314331]]0.012766935862600803
阅读更多...
Java 通过POI快速导入带图片的excel并且图片不会丢失

Java 通过POI快速导入带图片的excel并且图片不会丢失

## 通过POI快速导入带图片的excel并且图片不会丢失导入带图片的excel，这里也是研究了很久，在之前的博客中也有说明过，在项目使用过程中，发现很多时候导入响应很慢，而且每次导入图片都会丢失几张，所以又花了点时间研究修改了下，具体如下： 这边在导入时，通过自定义注解…
阅读更多...
java初学者踩得雷

java初学者踩得雷

目录 一段子父类调用重写的代码 1. 重写的代码 2. 执行结果 3. 分析原因 4. 总结概括 一段子父类调用重写的代码 这是一段有坑的代码&#xff0c;我们创建一个子类A和父类B&#xff0c;A中重写function方法&#xff0c;并且在B的构造方法中调用function 1. 重写的代码 …
阅读更多...
thinkphp5 原生sql查询及取返回值

thinkphp5 原生sql查询及取返回值

刚接触php&#xff0c;以前大量数据库都是直接写sql的&#xff0c;方便&#xff0c;好管理&#xff0c; 用thinkphp后&#xff0c;发现没有sql&#xff0c;对mvc模式还没深入了解&#xff0c;但这边要在上面写一些接口&#xff0c;有涉及数据库查询&#xff0c;修改等&#xf…
阅读更多...
【模式识别】计算机科学博士课程作业解析

【模式识别】计算机科学博士课程作业解析

作业二 2.1 最小风险贝叶斯决策分类计算 1、请给出以下问题的求解步骤&#xff0c;逐步给出计算过程&#xff1a; 已知条件为 P(w_1) 0.9 P(w_2)0.1 p(x|w_1)0.2 p(x|w_w)0.4 λ 11 0 \lambda_{11}0 λ11​0, λ 12 6 \lambda_{12}6 λ12​6 λ 21 1 \lambda_{21}1 …
阅读更多...
【postgresql】查看数据中表的信息

【postgresql】查看数据中表的信息

切换到postgresql数据库&#xff0c;各种不适应吧。 有个需求需要查询数据表的各种信息。 下面我们一起学习吧。 PostgreSQL: Documentation PostgreSQL: Documentation pg_namespace 存储名字空间。名字空间是 SQL 模式下层的结构&#xff1a;每个名字空间有独立的关系&am…
阅读更多...
NTTRU：兼容 NTT 算法的 NTRU-based KEM 方案

NTTRU：兼容 NTT 算法的 NTRU-based KEM 方案

参考文献&#xff1a; [CT65] Cooley J W, Tukey J W. An algorithm for the machine calculation of complex Fourier series[J]. Mathematics of computation, 1965, 19(90): 297-301.[Mont85] Montgomery P L. Modular multiplication without trial division[J]. Mathemat…
阅读更多...
⛳面试题-简述并分析ThreadLocalMap的key为什么是弱引用

⛳面试题-简述并分析ThreadLocalMap的key为什么是弱引用

⛳目录 简述 ThreadLocalMap 的 key 为弱引用的原因&#xff1a;分析&#xff1a;注意 &#xff1a; ThreadLocalMap 是 Java 中与 ThreadLocal 相关的一个重要类&#xff0c;用于在每个线程中存储和访问线程本地变量。在 ThreadLocalMap 中&#xff0c;key 为弱引用的主要原因…
阅读更多...
ModuleNotFoundError_ No module named ‘Crypto‘

ModuleNotFoundError_ No module named ‘Crypto‘

当要使用 python 进行加密数据的时候报错了 from Crypto.Util.Padding import pad, unpad from Crypto.Cipher import AES报错 File "F:\huisu.py", line 1, in <module>from Crypto.Util.Padding import pad, unpad ModuleNotFoundError: No module named Cr…
阅读更多...
千兆路由只有200M，原来是模式选择不对，也找到了内网不能通过动态域名访问内部服务的原因

千兆路由只有200M，原来是模式选择不对，也找到了内网不能通过动态域名访问内部服务的原因

本来1000M的宽带接入的&#xff0c;但是一测试发现只有200M&#xff0c;把电信叼了过来&#xff0c; 一测试发现宽带没问题&#xff0c;网线正常&#xff0c;网卡正常&#xff0c;只有可能是路由器的问题了&#xff0c;尴尬了&#xff0c;赶紧给满意好评放他走。回头好好研究一…
阅读更多...
企业年报API：打开企业经营大数据的新视角

企业年报API：打开企业经营大数据的新视角

引言 随着数字化转型的深入推进&#xff0c;企业年报API作为企业信息化建设中的重要组成部分&#xff0c;受到了越来越多企业和机构的关注和重视。而且&#xff0c;随着中国经济的快速发展&#xff0c;企业年报也成为投资者、监管机构以及相关利益方了解企业经营状况的重要途径…
阅读更多...
数据库管理-第116期 Oracle Exadata 06-ESS-下（202301114）

数据库管理-第116期 Oracle Exadata 06-ESS-下（202301114）

数据库管理-第116期 Oracle Exadata 06-ESS-下&#xff08;202301114&#xff09; 距离上一次正儿八经的技术分享又过了整整一周了&#xff0c;距离上一期Exadata专题文章也过了11天了&#xff0c;今天一鼓作气把ESS写完&#xff0c;毕竟明天又要飞北京了。 1 Smart Scan 其…
阅读更多...
H5三网魔幻手游【众神传奇】win服务端+GM授权后台+架设教程

H5三网魔幻手游【众神传奇】win服务端+GM授权后台+架设教程

搭建资源下载地址&#xff1a;H5三网魔幻手游【众神传奇】win服务端GM授权后台架设教程-海盗空间
阅读更多...
安全好用性价比高的远程协同运维软件有吗？

安全好用性价比高的远程协同运维软件有吗？

据悉不少IT专业人员认为&#xff0c;远程运维风险性更高&#xff0c;更容易给企业带来更大的风险。所以不少运维人员都在求一款安全好用性价比高的远程协同运维软件&#xff0c;因为下班需要&#xff0c;因为碰到IT难题时候需要&#xff0c;因为驻场需要。那你知道市面上安全好…
阅读更多...
macOS 13.6 及后续系统安装 Asahi Linux 将破坏引导

macOS 13.6 及后续系统安装 Asahi Linux 将破坏引导

导读Asahi Linux 是一个致力于为 Apple Silicon 设备带来 Linux 支持的项目&#xff0c;日前有用户反馈称&#xff0c;若在相关设备上安装了 macOS 13.6-14&#xff0c;再安装 Asahi Linux &#xff0c;就会导致系统引导失败&#xff0c;出现“黑屏”情况。 目前 Asahi Linux 项…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023