什么是贪心算法

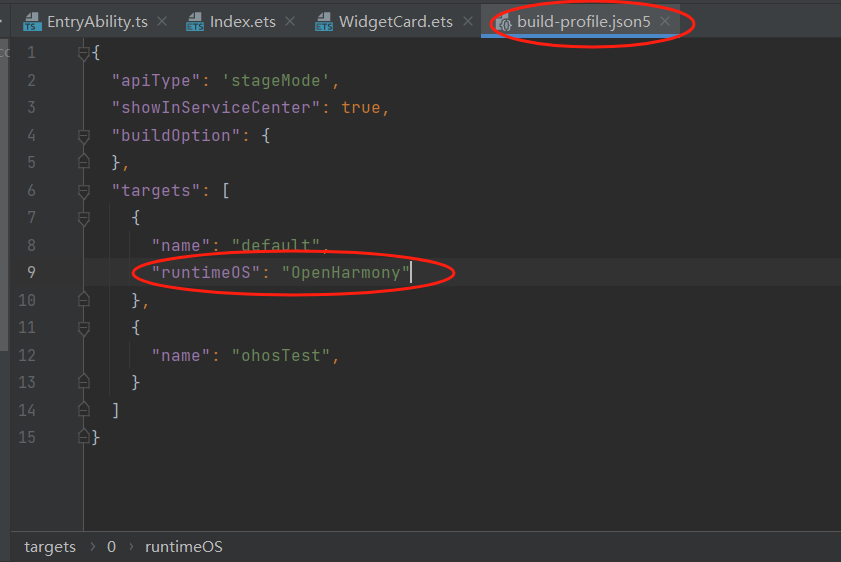
分配饼干例题

//贪心算法
//保证局部最优，从而使最后得到的结果是全局最优的

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1001;
int main()
{
   
	int fin(int a[], int b[]);

	int n, m;//n表示的是孩子的饥饿数，m表示的是饼干
	int a[N], b[N];
	for (int i = 0; i < n; i++)
	{
   
		cin >> a[i];
	}
	for (int j = 0; j < m; j++)
	{
   
		cin >> b[j];
	}
	sort(a, a + n);//都需要进行排序
	sort(b, b + m);  
	printf("%d\n", find(a, b));//找到可以吃饱的孩子的数目  

}
int find(int*a, int*b)  
{
   
	int a1= 0;//能吃饱孩子的数目  
	int b1 = 0;//饼干的下标  
	while (a1 < a.length() && b1 < b.length())  
	{
   
		if (a[a1] <= b[b1++]) a1++;  
	}
	return a1;  

}

理解二

1. 当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性。
   运用贪心策略在每一次转化时都取得了最优解。问题的最优子结构性质是该问题可用贪心算法求解的关键特征。贪心算法的每一次操作都对结果产生直接影响。贪心算法对每个子问题的解决方案都做出选择，不能回退。

   2. 贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。

3.实际上，贪心算法适用的情况很少。一般对一个问题分析是否适用于贪心算法，可以先选择该问题下的几个实 际数据进行分析，就可以做出判断。

4.当发现一个问题的解决只需要考虑最优子结构的问题即可，即每一步最优，不需要考虑整体，而这时就可以用我们的贪心算法来解决问题。

例子（局部——》整体）
选择排序

分割字符串

分割平衡字符串

大佬思路
class Solution {
   
public:
    int balancedStringSplit(string s) {
   
     int balance =0;  
     int count =0;    
     for(int i =0;i<s.size();i++){
       
         if(s[i