使用opencv实现图像的畸形矫正：仿射变换

news2024/11/17 5:31:27

1 仿射变换

1.1 什么是仿射变换

在图像处理中，经常需要对图像进行各种操作如平移、缩放、旋转、翻转等，这些都是图像的仿射变换。图像仿射变换又称为图像仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。通常图像的旋转加上拉升就是图像仿射变换，仿射变换需要一个M矩阵实现，但是由于仿射变换比较复杂，很难找到这个M矩阵.

1.2 仿射变换的数学表达

仿射变换也称仿射投影，是指几何中，对一个向量空间进行线性变换并接上一个平移，变换为另一个向量空间。所以，仿射变换其实也就是再讲如何来进行两个向量空间的变换
假设有一个向量空间k：

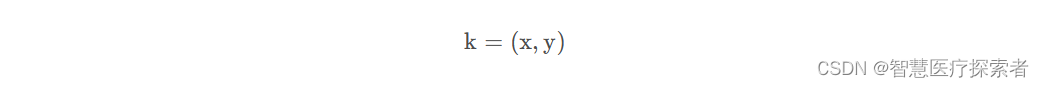
还有一个向量空间j：

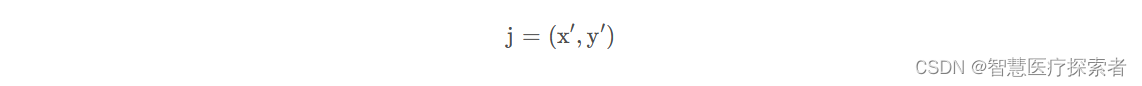
 如果我们想要将向量空间由k变为j，可以通过下面的公式进行变换

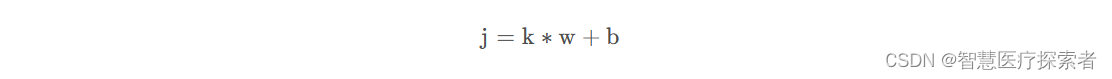
将上式进行拆分可得

 

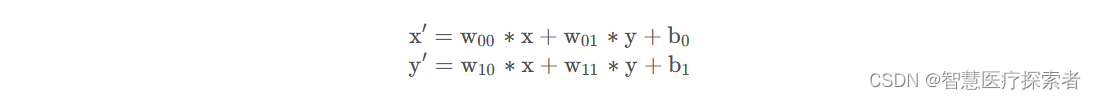
我们再将上式转换为矩阵的乘法 

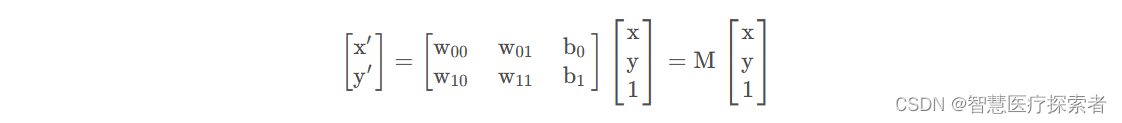
通过参数矩阵M就可以实现两个向量空间之间的转换，在进行仿射变换的时候我们也只需要一个矩阵M就可以实现平移、缩放、旋转和翻转变换。

1.3 opencv中的仿射变换

OpenCV中使用warpAffine函数来实现仿射变换

cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) → dst
  • src：输入的图像数组
  • M：仿射变换矩阵
  • dsize：变换后图像的大小
  • flags：使用的插值算法
  • borderValue：边界的填充值

1.3.1 图像平移

在平面坐标系有点P(x,y)和点P′(x′,y′)，如果我们想要将P点移动到P'，通过下面的变换就可以实现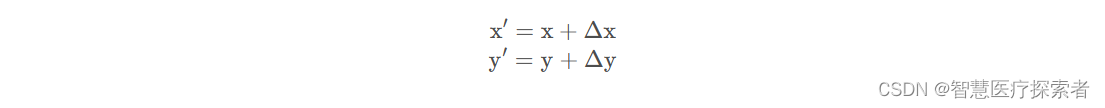

 其中Δx和Δy就是x方向上和y方向上的偏移量，我们将其转换为矩阵的形式

 上面的矩阵M就是仿射变换的平移参数，使用OpenCV中的warpAffine函数实现如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt


def show_cmp_img(original_img,transform_img):
    _, axes = plt.subplots(1, 2)
    # 显示图像
    axes[0].imshow(original_img)
    axes[1].imshow(transform_img)
    # 设置子标题
    axes[0].set_title("original image")
    axes[1].set_title("transform image")
    plt.show()


# 定义一个图像平移矩阵
# x向左平移(负数向左,正数向右)100
# y向下平移(负数向上,正数向下)200个像素
M = np.array([[1, 0, -100], [0, 1, 200]], dtype=np.float)

# 读取需要平移的图像
img = cv2.imread("../data/girl02.jpg")

# 将图片由BGR转为RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 定义平移后图像的大小,保持和原图大小一致
dsize = img.shape[:2][::-1]

# 便于大家观察这里采用白色来填充边界
translation_img = cv2.warpAffine(img, M, dsize, borderValue=(255, 255, 255))

# 显示图像
show_cmp_img(img, translation_img)

运行结果显示如下：

1.3.2 图像翻转

使用opencv的仿射变换实现图像的水平翻转、垂直翻转、镜像反转（同时进行水平和垂直翻转）

上图中的A、B、C、D表示图像的四个顶点，如果我们需要对图像进行水平翻转，那么我们就需要将 A点和B点进行交换，C点和D点进行交换，沿着x轴的中线进行对称交换位置，通过下面的式子可以实现水平翻转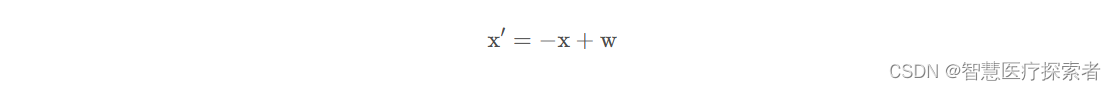

上式中的w表示图像的宽度，同理可得垂直翻转的实现公式

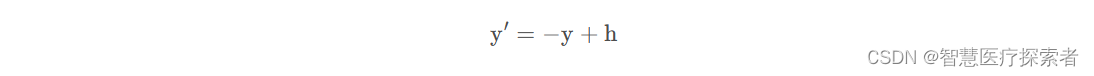
上式中的h表示的是图像的高，图像翻转的变换矩阵：

使用OpenCV中的warpAffine函数实现如下：

import cv2
import matplotlib.pyplot as plt
import numpy as np


def show_cmp_img(original_img,transform_img):
    _, axes = plt.subplots(1, 2)
    # 显示图像
    axes[0].imshow(original_img)
    axes[1].imshow(transform_img)
    # 设置子标题
    axes[0].set_title("original image")
    axes[1].set_title("transform image")
    plt.show()


horizontal_flip = True
vertical_flip = True

img = cv2.imread("../data/girl02.jpg")

# 获取输入图片的宽和高
height,width = img.shape[:2]

# 初始化变换矩阵
M = np.array([[0, 0, 0], [0, 0, 0]], dtype=np.float)

# 水平翻转
if horizontal_flip:
    M[0] = [-1, 0, width]

# 垂直翻转
if vertical_flip:
    M[1] = [0, -1, height]

# 将图片由BGR转为RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 定义缩放后图片的大小
img_flip = cv2.warpAffine(img, M, (width, height))

show_cmp_img(img, img_flip)

运行结果显示如下：

OpenCV的flip函数翻转图像

flip函数参数：

  • src：输入的图像数组
  • flipCode：图像翻转参数，1表示水平翻转，0表示垂直翻转，-1表示镜像翻转
img = cv2.imread("../data/girl02.jpg")

#水平翻转
horizontal_flip_img = cv2.flip(img,1)

#垂直翻转
vertical_flip_img = cv2.flip(img,0)

#镜像翻转
mirror_flip_img = cv2.flip(img,-1)

numpy的索引翻转图像

img = cv2.imread("../data/girl02.jpg")

#水平翻转
horizontal_flip_img = img[:,::-1]

#垂直翻转
vertical_flip_img = img[::-1]

#镜像翻转
mirror_flip_img = img[::-1,::-1]

 1.3.3 图像缩放

如果我们想要对坐标系的P点进行缩放操作，通过下面的公式就可以实现

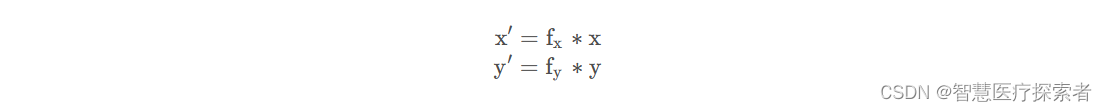
 通过，在x和y前面添加一个缩放系数即可，同样我们将其转换为矩阵形式

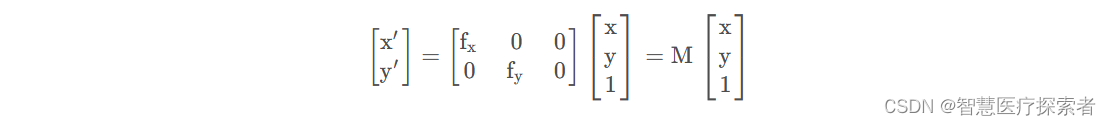
通过上面的矩阵M我们就可以实现对图片的缩放，使用OpenCV中的warpAffine函数实现如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt


def show_cmp_img(original_img,transform_img):
    _, axes = plt.subplots(1, 2)
    # 显示图像
    axes[0].imshow(original_img)
    axes[1].imshow(transform_img)
    # 设置子标题
    axes[0].set_title("original image")
    axes[1].set_title("transform image")
    plt.show()


# 定义宽缩放的倍数
fx = 0.5

# 定义高缩放的倍数
fy = 2

# 定义一个图像缩放矩阵
M = np.array([[fx, 0, 0], [0, fy, 0]], dtype=np.float)

# 读取图像
img = cv2.imread("../data/girl02.jpg")

# 获取图片的宽和高
height, width = img.shape[:2]

# 将图片由BGR转为RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 定义缩放后图片的大小
scale_img = cv2.warpAffine(img, M, (int(width*fx), int(height*fy)))

# 显示图像
show_cmp_img(img, scale_img)

结果显示如下：

opencv中的resize函数也能实现一样的效果。

1.3.4 图像旋转

围绕原点旋转：我们先来看看一个二维平面上的点在围绕原点是如何旋转的

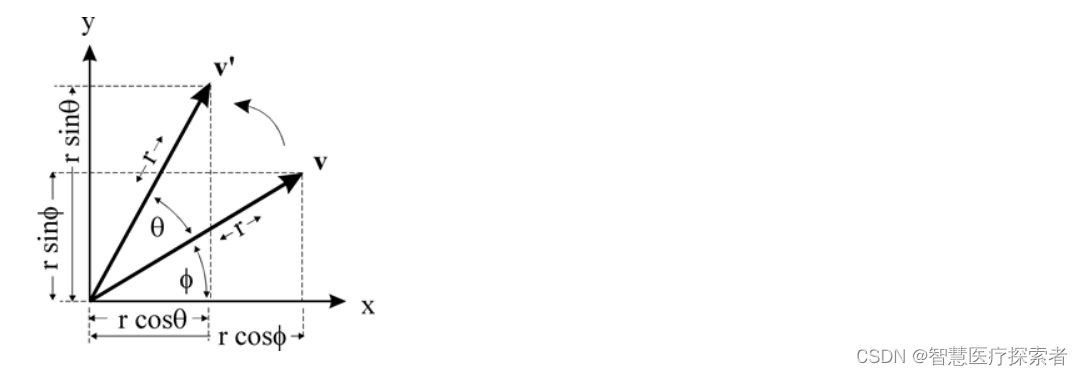
上图中点v在围绕原点旋转θ度之后得到了点v′，我们将坐标点用极坐标的形式来表示可以得到 v(rcosϕ,rsinϕ)，所以v′(rcos(θ+ϕ),rsin(θ+ϕ))利用正弦和余弦将其展开可得

然后再将上式用矩阵M表示，可得

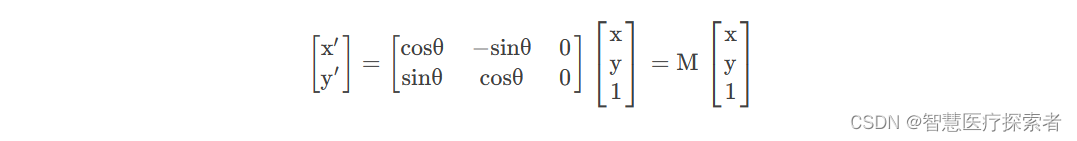
特别注意：我们在建立直角坐标系的时候是以左下角为原点建立的，然而对于图像而言是以左上角为原点建立的，所以我们需要对角度θ进行取反，结合三角函数的特性，M矩阵的表达式如下

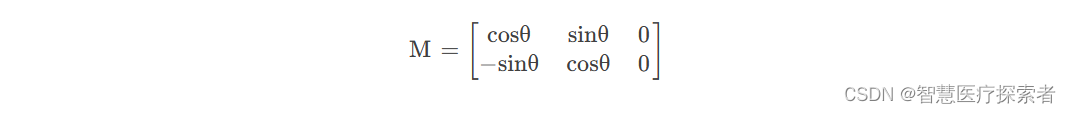
还需要注意的是这里的角度都是弧度制，所以我们还需要对其进行转换，转换代码如下

#将角度转换为弧度制
radian_theta = theta/180 * np.pi

将图片围绕原点进行逆时针旋转θ度，opencv的代码实现如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt


def show_cmp_img(original_img,transform_img):
    _, axes = plt.subplots(1, 2)
    # 显示图像
    axes[0].imshow(original_img)
    axes[1].imshow(transform_img)
    # 设置子标题
    axes[0].set_title("original image")
    axes[1].set_title("transform image")
    plt.show()


theta = 30

# 将角度转换为弧度制
radian_theta = theta/180 * np.pi

# 定义围绕原点旋转的变换矩阵
M = np.array([[np.cos(radian_theta), np.sin(radian_theta), 0],
             [-np.sin(radian_theta), np.cos(radian_theta), 0]])
# 读取图像
img = cv2.imread("../data/girl02.jpg")

# 定义旋转后图片的宽和高
height, width = img.shape[:2]

# 将图片由BGR转为RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 围绕原点逆时针旋转\theta度
rotate_img = cv2.warpAffine(img, M, (width, height))

# 显示图像
show_cmp_img(img,rotate_img)

 运行结果显示如下：

1.3.5 围绕任意点旋转

下图的v点在围绕点(a,b)旋转90度得到v′。可以将其等价于先将v点平移到v1​点，然后再将v1​点围绕原点旋转90度得到v2​点，最后再将v2​点沿着v点平移的反方向平移相同长度，最终得到v′。这样我们就将围绕任意坐标点旋转的问题转换成了围绕原点旋转的问题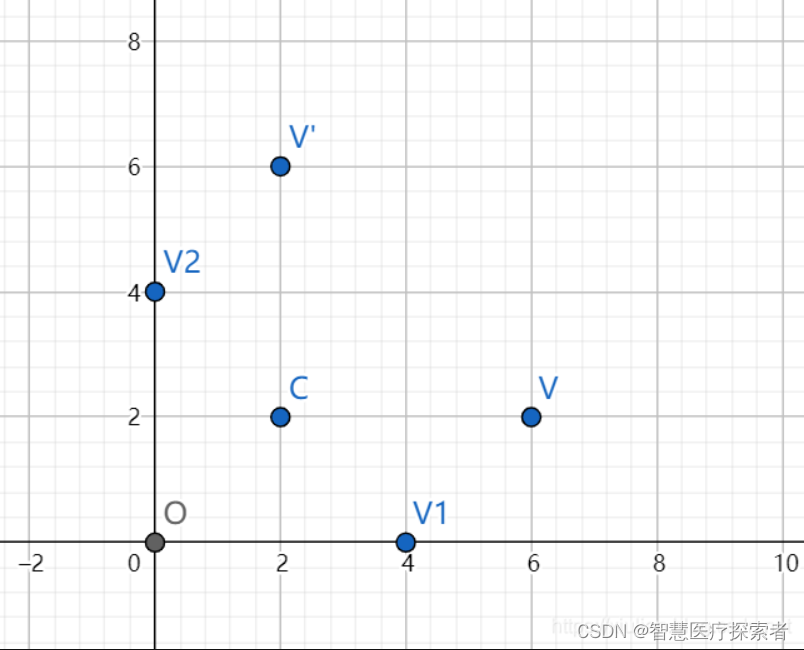

我们来回顾一下，围绕原点旋转坐标的变换公式：

 

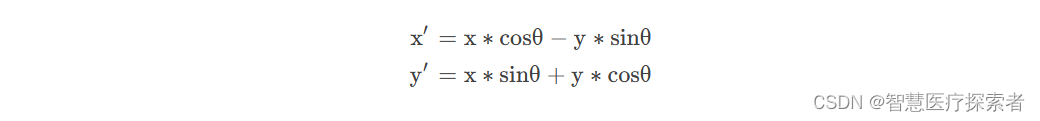
在围绕原点旋转变换公式的基础上，我们将其改进为围绕任意点c(a,b)旋转，我们现在原来的坐标进行平移，得到变换后的坐标，最后再沿着之前平移的反方向进行平移，就得到围绕任意点旋转的变换公式：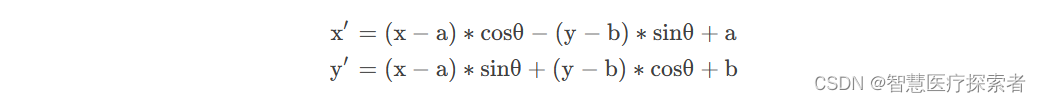

将其展开可得

 

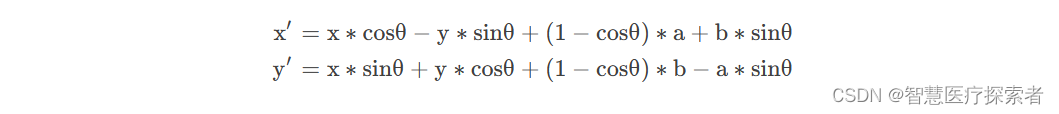
将上式用矩阵M表示： 

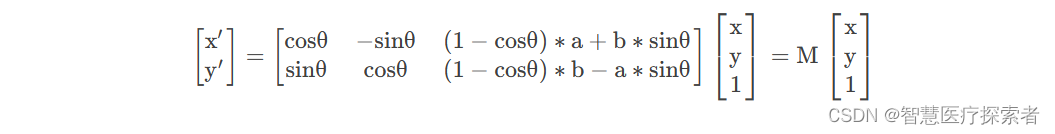
上式中的c(a,b)表示旋转中心，因为坐标系问题需要对θ进行取反，最终M矩阵的表达式如下

使用opencv的代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt


def show_cmp_img(original_img,transform_img):
    _, axes = plt.subplots(1, 2)
    # 显示图像
    axes[0].imshow(original_img)
    axes[1].imshow(transform_img)
    # 设置子标题
    axes[0].set_title("original image")
    axes[1].set_title("transform image")
    plt.show()


img = cv2.imread("../data/girl02.jpg")

theta = 30
height, width = img.shape[:2]

# 定义围绕图片的中心旋转
point_x, point_y = int(width/2), int(height/2)

# 将角度转换为弧度制
radian_theta = theta / 180 * np.pi

# 定义围绕任意点旋转的变换矩阵
M = np.array([[np.cos(radian_theta), np.sin(radian_theta),
               (1-np.cos(radian_theta))*point_x-point_y*np.sin(radian_theta)],
              [-np.sin(radian_theta), np.cos(radian_theta),
               (1-np.cos(radian_theta))*point_y+point_x*np.sin(radian_theta)]])

# 将图片由BGR转为RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 定义旋转后图片的宽和高
height, width = img.shape[:2]

# 围绕原点逆时针旋转\theta度
rotate_img = cv2.warpAffine(img, M, (width, height))

# 显示图像
show_cmp_img(img, rotate_img)

运行结果显示如下：

围绕图像中心旋转后的图片部分被裁剪掉了，如果我们想让旋转之后的图片仍然是完整，代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt


def show_cmp_img(original_img,transform_img):
    _, axes = plt.subplots(1, 2)
    # 显示图像
    axes[0].imshow(original_img)
    axes[1].imshow(transform_img)
    # 设置子标题
    axes[0].set_title("original image")
    axes[1].set_title("transform image")
    plt.show()


img = cv2.imread("../data/girl02.jpg")

theta = 30
is_completed = True
height, width = img.shape[:2]

# 定义围绕图片的中心旋转
point_x, point_y = int(width/2), int(height/2)

# 将角度转换为弧度制
radian_theta = theta / 180 * np.pi

# 定义围绕任意点旋转的变换矩阵
M = np.array([[np.cos(radian_theta), np.sin(radian_theta),
               (1-np.cos(radian_theta))*point_x-point_y*np.sin(radian_theta)],
              [-np.sin(radian_theta), np.cos(radian_theta),
               (1-np.cos(radian_theta))*point_y+point_x*np.sin(radian_theta)]])
# 将图片由BGR转为RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 定义旋转后图片的宽和高
height, width = img.shape[:2]

# 判断旋转之后的图片是否需要保持完整
if is_completed:
    # 增大旋转之后图片的宽和高,防止被裁剪掉
    new_height = height * np.cos(radian_theta) + width * np.sin(radian_theta)
    new_width = height * np.sin(radian_theta) + width * np.cos(radian_theta)

    # 增大变换矩阵的平移参数
    M[0, 2] += (new_width - width) * 0.5
    M[1, 2] += (new_height - height) * 0.5
    height = int(np.round(new_height))
    width = int(np.round(new_width))
# 围绕原点逆时针旋转\theta度
rotate_img = cv2.warpAffine(img, M, (width, height))
# 显示图像
show_cmp_img(img, rotate_img)

运行结果显示如下：

2 使用opencv实现图像的畸形矫正

在日常处理图片过程中，我们经常遇到扭曲的图片，首先我们要对扭曲的图片进行校正，然后在送入深度模型进行处理，扭曲的图片如下所示：

为实现将倾斜的目标矫正过来，首先，我们需要使用轮廓检测等方法获取到目标的4个关键点坐标值；然后利用相应的变换获取到新的4个坐标点；接着利用这4对关键点计算出仿射变换矩阵M；最后应用仿射变换矩阵到目标中即可。步骤如下：

  • 读取输入图片；
  • 获取原始目标的4个坐标点（左上，左下，右上，右下）；
  • 通过4个坐标点计算出新的坐标点；
  • 使用opencv计算仿射变换矩阵M；
  • 应用仿射变换进行变换并进行结果显示。

2.1 获取四个顶点坐标

def get4points(img: np.ndarray, thed, n):
    # 灰度和二值化
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    ret, binary = cv2.threshold(gray, thed, 255, cv2.THRESH_BINARY)

    # 搜索轮廓
    contours, hierarchy = cv2.findContours(
        binary,
        cv2.RETR_LIST,
        cv2.CHAIN_APPROX_SIMPLE)

    # 按轮廓长度选取需要轮廓
    len_list = []
    for i in range(len(contours)):
        len_list.append(len(contours[i]))

    # 选第二长的
    sy = np.argsort(np.array(len_list))[-n]

    # 寻找顶点
    sum_list = []
    dif_list = []
    for i in contours[sy]:
        sum = i[0][0]+i[0][1]
        sum_list.append(sum)
        dif_list.append(i[0][0]-i[0][1])

    id_lb = np.argsort(np.array(sum_list))
    id_lb2 = np.argsort(np.array(dif_list))
    lu_id , rd_id = id_lb[0], id_lb[-1]
    ld_id , ru_id = id_lb2[0], id_lb2[-1]

    points = np.array([contours[sy][lu_id][0], contours[sy][rd_id][0],
                       contours[sy][ld_id][0], contours[sy][ru_id][0]])

    return points, contours, sy

2.2 仿射变换

def four_point_transform(image, pts):
    # 获取坐标点，并将它们分离开来
    rect = order_points(pts)
    (tl, tr, br, bl) = rect
    # 计算新图片的宽度值，选取水平差值的最大值
    widthA = np.sqrt(((br[0] - bl[0]) ** 2) + ((br[1] - bl[1]) ** 2))
    widthB = np.sqrt(((tr[0] - tl[0]) ** 2) + ((tr[1] - tl[1]) ** 2))
    maxWidth = max(int(widthA), int(widthB))

    # 计算新图片的高度值，选取垂直差值的最大值
    heightA = np.sqrt(((tr[0] - br[0]) ** 2) + ((tr[1] - br[1]) ** 2))
    heightB = np.sqrt(((tl[0] - bl[0]) ** 2) + ((tl[1] - bl[1]) ** 2))
    maxHeight = max(int(heightA), int(heightB))

    # 构建新图片的4个坐标点
    dst = np.array([
        [0, 0],
        [maxWidth - 1, 0],
        [maxWidth - 1, maxHeight - 1],
        [0, maxHeight - 1]], dtype="float32")

    # 获取仿射变换矩阵并应用它
    M = cv2.getPerspectiveTransform(rect, dst)
    # 进行仿射变换
    warped = cv2.warpPerspective(image, M, (maxWidth, maxHeight))

    # 返回变换后的结果
    return warped

2.3 完整代码

# coding=utf-8
import numpy as np
import cv2
import matplotlib.pyplot as plt


def get4points(img: np.ndarray, thed, n):
    # 灰度和二值化
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    ret, binary = cv2.threshold(gray, thed, 255, cv2.THRESH_BINARY)

    # 搜索轮廓
    contours, hierarchy = cv2.findContours(
        binary,
        cv2.RETR_LIST,
        cv2.CHAIN_APPROX_SIMPLE)

    # 按轮廓长度选取需要轮廓
    len_list = []
    for i in range(len(contours)):
        len_list.append(len(contours[i]))

    # 选第二长的
    sy = np.argsort(np.array(len_list))[-n]

    # 寻找顶点
    sum_list = []
    dif_list = []
    for i in contours[sy]:
        sum = i[0][0]+i[0][1]
        sum_list.append(sum)
        dif_list.append(i[0][0]-i[0][1])

    id_lb = np.argsort(np.array(sum_list))
    id_lb2 = np.argsort(np.array(dif_list))
    lu_id , rd_id = id_lb[0], id_lb[-1]
    ld_id , ru_id = id_lb2[0], id_lb2[-1]

    points = np.array([contours[sy][lu_id][0], contours[sy][rd_id][0],
                       contours[sy][ld_id][0], contours[sy][ru_id][0]])

    return points, contours, sy


def order_points(pts):
    # 初始化坐标点
    rect = np.zeros((4, 2), dtype = "float32")

    # 获取左上角和右下角坐标点
    s = pts.sum(axis = 1)
    rect[0] = pts[np.argmin(s)]
    rect[2] = pts[np.argmax(s)]

    # 分别计算左上角和右下角的离散差值
    diff = np.diff(pts, axis = 1)
    rect[1] = pts[np.argmin(diff)]
    rect[3] = pts[np.argmax(diff)]

    return rect


def four_point_transform(image, pts):
    # 获取坐标点，并将它们分离开来
    rect = order_points(pts)
    (tl, tr, br, bl) = rect
    # 计算新图片的宽度值，选取水平差值的最大值
    widthA = np.sqrt(((br[0] - bl[0]) ** 2) + ((br[1] - bl[1]) ** 2))
    widthB = np.sqrt(((tr[0] - tl[0]) ** 2) + ((tr[1] - tl[1]) ** 2))
    maxWidth = max(int(widthA), int(widthB))

    # 计算新图片的高度值，选取垂直差值的最大值
    heightA = np.sqrt(((tr[0] - br[0]) ** 2) + ((tr[1] - br[1]) ** 2))
    heightB = np.sqrt(((tl[0] - bl[0]) ** 2) + ((tl[1] - bl[1]) ** 2))
    maxHeight = max(int(heightA), int(heightB))

    # 构建新图片的4个坐标点
    dst = np.array([
        [0, 0],
        [maxWidth - 1, 0],
        [maxWidth - 1, maxHeight - 1],
        [0, maxHeight - 1]], dtype="float32")

    # 获取仿射变换矩阵并应用它
    M = cv2.getPerspectiveTransform(rect, dst)
    # 进行仿射变换
    warped = cv2.warpPerspective(image, M, (maxWidth, maxHeight))

    # 返回变换后的结果
    return warped


def show_cmp_img(original_img, transform_img):
    _, axes = plt.subplots(1, 2)
    # 显示图像
    axes[0].imshow(original_img)
    axes[1].imshow(transform_img)
    # 设置子标题
    axes[0].set_title("original image")
    axes[1].set_title("transform image")
    plt.show()


# 读取图片
image = cv2.imread('../data/warp01.png')

points, _, _ = get4points(image, 127, 1)

# 获取原始的坐标点
pts = np.array(points, dtype="float32")

# 对原始图片进行变换
warped = four_point_transform(image, pts)

show_cmp_img(image, warped)

运行结果显示如下：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1205480.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

面试：容器技术

面试：容器技术

目录 为什么需要 DevOpsDocker 是什么？Docker 与虚拟机有何不同？什么是 Docker 镜像？什么是 Docker 容器？Docker 容器有几种状态？解释一下 Dockerfile 的 ONBUILD 指令？什么是 Docker Swarm？如何…
阅读更多...
SSH全能终端工具mobaXterm（远程工具）使用教程

SSH全能终端工具mobaXterm（远程工具）使用教程

参考文章：SSH全能终端工具MobaXterm Personal v23.0 完全汉化绿色版 参考文章：MobaXterm 23终端控制软件 文章目录 SSH全能终端工具mobaXterm使用教程目录引言mobaXterm概述安装与配置下载mobaXterm安装过程基础设置 SSH连接创建SSH会话SSH命令行操作文…
阅读更多...
Azure 机器学习：在 Azure 机器学习中使用 Azure OpenAI 模型

Azure 机器学习：在 Azure 机器学习中使用 Azure OpenAI 模型

目录 一、环境准备二、Azure 机器学习中的 OpenAI 模型是什么？三、在机器学习中访问 Azure OpenAI 模型连接到 Azure OpenAI部署 Azure OpenAI 模型 四、使用自己的训练数据微调 Azure OpenAI 模型使用工作室微调微调设置训练数据自定义微调参数部署微调的模型 使用…
阅读更多...
线圈寿命预测 数据集讲解

线圈寿命预测 数据集讲解

来自-郭师兄 1.这个是线圈数据的阻抗、电抗等数据，我想根据这个个数据进行线圈寿命预测也就是RUL预测，请问有什么思路吗。 最简单的思路： 数据通过某种方法进行压缩表征到一维再通过 同时需要标签。 确定一个特征 使用降维方法如同PCA来构…
阅读更多...
点大商城V2版 2.5.3全插件开源独立版 百度+支付宝+QQ+头条+小程序端+unipp开源端安装测试教程

点大商城V2版 2.5.3全插件开源独立版 百度+支付宝+QQ+头条+小程序端+unipp开源端安装测试教程

点大商城V2是一款采用全新界面设计支持多端覆盖的小程序应用，支持H5、微信公众号、微信小程序、头条小程序、支付宝小程序、百度小程序，本程序是点大商城V2独立版，包含全部插件，代码全开源，并且有VUE全端代码。 适用范…
阅读更多...
No200.精选前端面试题，享受每天的挑战和学习

No200.精选前端面试题，享受每天的挑战和学习

🤍 前端开发工程师（主业）、技术博主（副业）、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…
阅读更多...
vscode launch.json

vscode launch.json

有时新的服务器进行调试时，需要设置调试的launch.json的结果 然后就可以打开一个launch.json 其内容如下 {// 使用 IntelliSense 了解相关属性。 // 悬停以查看现有属性的描述。// 欲了解更多信息，请访问: https://go.microsoft.com/fwlink/?linkid83…
阅读更多...
【Axure高保真原型】3D饼图_移入显示数据标签

【Axure高保真原型】3D饼图_移入显示数据标签

今天和大家分享3D饼图_移入显示数据标签的原型模板，鼠标移入扇形区域时，对应区域会变绿，可以查看该区域对应的项目、数据和占比，这个原型模板是用Axure原生元件制作的，所以无需联网，而且可以自由修改样式、…
阅读更多...
数据结构哈希表（散列）Hash，手写实现（图文推导）

数据结构哈希表（散列）Hash，手写实现（图文推导）

目录 一、介绍 二、哈希数据结构 三、✍️实现哈希散列 1. 哈希碰撞💥 2. 拉链寻址⛓️ 3. 开放寻址⏩ 4. 合并散列 一、介绍 哈希表，也被称为散列表，是一种重要的数据结构。它通过将关键字映射到一个表中的位置来直接访问记录&#…
阅读更多...
HarmonyOS开发(三)：ArkTS基础

HarmonyOS开发(三)：ArkTS基础

1、ArkTS演进 Mozilla创建了JS ---> Microsoft创建了TS ----> Huawei进一步推出ArkTS 从最初的基础逻辑交互（JS）,到具备类型系统的高效工程开发（TS）,再到融合声明式UI、多维状态管理等丰富的应用开发能力&…
阅读更多...
高速高精运动控制，富唯智能AI边缘控制器助力自动化行业变革

高速高精运动控制，富唯智能AI边缘控制器助力自动化行业变革

随着工业大数据时代的到来，传统控制与决策方式无法满足现代数字化工厂对工业大数据分析与决策的需求，AI边缘控制器赋能现代化智慧工厂，实现工业智造与行业变革。 富唯智能AI边缘控制器，基于x86架构的IPC形态产品，通过…
阅读更多...
【python自动化】Playwright基础教程(七)Keyboard键盘

【python自动化】Playwright基础教程(七)Keyboard键盘

【python自动化】Playwright基础教程(七)Keyboard键盘 playwright模拟键盘操作 键盘事件提供了用于管理虚拟键盘的API，高级API是keyboard.type()，它使用的是原始字符再页面上生成对应的keydown 、 keypress / input 和 keyup 事件。 模拟真实键盘操作进行…
阅读更多...
Java面向对象（进阶）-- Object类的详细概述

Java面向对象（进阶）-- Object类的详细概述

文章目录 一、如何理解根父类二、 Object类的方法（1）引子（2）Object类的说明 三、了解的方法（1）clone( )1、介绍2、举例 （2）finalize( )1、介绍2、举例 （3）get…
阅读更多...
windows系统用于 SDN 的软件负载均衡器 (SLB)

windows系统用于 SDN 的软件负载均衡器 (SLB)

适用于：Azure Stack HCI 版本 22H2 和 21H2；Windows Server 2022、Windows Server 2019、Windows Server 2016 软件负载均衡器包括哪些内容？ 软件负载均衡器提供以下功能： 适用于北/南和东/西 TCP/UDP 流量的第 4 层 (L4) 负载均…
阅读更多...
什么是会话固定以及如何在 Node.js 中防止它

什么是会话固定以及如何在 Node.js 中防止它

什么是会话固定以及如何在 Node.js 中防止它 在深入讨论之前，我们需要了解会话是什么以及会话身份验证如何工作。 什么是会话？ 正如我们所知，HTTP 请求是无状态的，这意味着当我们发送登录请求时，并且我们有有效的用…
阅读更多...
@CacheInvalidate(name = “xxx“, key = “#results.![a+b]“,multi = true)是什么意思

@CacheInvalidate(name = “xxx“, key = “#results.![a+b]“,multi = true)是什么意思

@CacheInvalidate 注解是 JetCache 框架提供的注解，它是由阿里巴巴开源的组织 Alibaba Group 开发和维护的。JetCache 是一款基于注解的缓存框架，提供了丰富的缓存功能和灵活的配置选项，可用于增强应用程序的性能和可扩展性。JetCache 支持多种缓存后端，包括内存缓存、Redi…
阅读更多...
2023亚太杯数学建模C题思路分析

2023亚太杯数学建模C题思路分析

文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 （赛题出来以后第一时间在CSDN分享） https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…
阅读更多...
二十、泛型（6）

二十、泛型（6）

本章概要 问题 任何基本类型都不能作为类型参数实现参数化接口转型和警告重载基类劫持接口 自限定的类型 古怪的循环泛型自限定参数协变 问题 本节将阐述在使用 Java 泛型时会出现的各类问题。 任何基本类型都不能作为类型参数 正如本章早先提到的，Java 泛型的…
阅读更多...
OpenCV 笔记(6)：像素间的基本关系——邻域、邻接、通路、连通、距离

OpenCV 笔记(6)：像素间的基本关系——邻域、邻接、通路、连通、距离

像素是图像的基本元素，像素与像素之间存在着某些联系，理解像素间的基本关系是数字图像处理的基础。常见的像素间的基本关系包括：邻域、邻接、通路、连通、距离。 Part11. 邻域 邻域表示了像素之间的连接关系。 像素(x,y)的邻域，是…
阅读更多...
Linux技能篇-软链接和硬链接

Linux技能篇-软链接和硬链接

文章目录 前言一、硬链接是什么？二、软链接是什么？三、硬链接和软链接的区别和共性1.区别2.共同点 总结 前言 在Linux系统中，有两个容易混淆的概念，就是软链接（Soft Link）和硬链接（Hard Link&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023