最后一期单调队列了啊
目录
题目:琪露诺
思路:
题目:选数游戏
思路:
题目:寻找段落
思路:
之前做的都是连续的长度区间求最值,今天体验一下不连续的区间。
然后就是要注意维护单调队列时维护的是哪个数组?在的哪个区间?
题目:琪露诺


思路:
首先f[i]表示走到i格子时获得最大和:f[i]=max(f[i-r]~f[i-l])+v[i]
常规做法O(n^2)会超时 那就维护f数组在[i-r,i-l]的单调队列,当遍历i时,维护f[i-r,i-l]的最大值的单调队列,不是原数组v!!!
入队新元素为i-l 所以h<=t&&f[q[t]]<f[i-l],队尾才能出队,然后i-l入队
队头过期元素和i-r比较 所以h<=t&&q[h]<i-r,队头下标比i-r还小就要丢掉
更新f[i]:f[i]=f[q[h]]+v[i]
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+86;
int n,f[N],l,r,ans=-0x3f3f3f3f,v[N],q[N],h=1,t=0;//其实h和t的值不重要,只要h==t就是队中仅1个元素,h>t队空,里面存放的下标才是关键
//有负数所以 ans 初始化为负无穷
int main()
{
memset(f,-0x3f,sizeof(f));f[0]=0;
scanf("%d%d%d",&n,&l,&r);
for(int i=0;i<=n;i++)
scanf("%d",&v[i]);
for(int i=l;i<=n;i++)//遍历到i时,我们的新入队元素应该是i-l,不是i
{
while(h<=t&&q[h]<i-r) h++;//过期队头出队
while(h<=t&&f[q[t]]<f[i-l]) t--;//维护[i-r,i-l]的单调最值
q[++t]=i-l;//新元素i-l入队
f[i]=f[q[h]]+v[i];//从最值中取出更新f[i]
if(i+r>n) //及时更新答案
ans=max(f[i],ans);
}
printf("%d\n",ans);
return 0;
}
可以欣赏一下这个超时版本
//朴素版本: 超时版本
#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+1;
int n,l,r,a[maxn],f[maxn],ans=-1<<30;
int main()
{
scanf("%d%d%d",&n,&l,&r);
for(int i=0;i<=n;i++) scanf("%d",&a[i]);
memset(f,0xcf,sizeof(f));f[0]=0;//由于冰冻指数可能是负数,所以一定要记得初始化
for(int i=l;i<=n+r-1;i++)//第一步至少跳到第l格,最后一步至多跳到第n+r-1格
{
for(int j=max(0,i-r);j<=i-l;j++) f[i]=max(f[i],f[j]+a[i]);
if(i>=n) ans=max(ans,f[i]);//已经跳到对岸了再更新答案
}
printf("%d",ans);
return 0;
}
题目:选数游戏
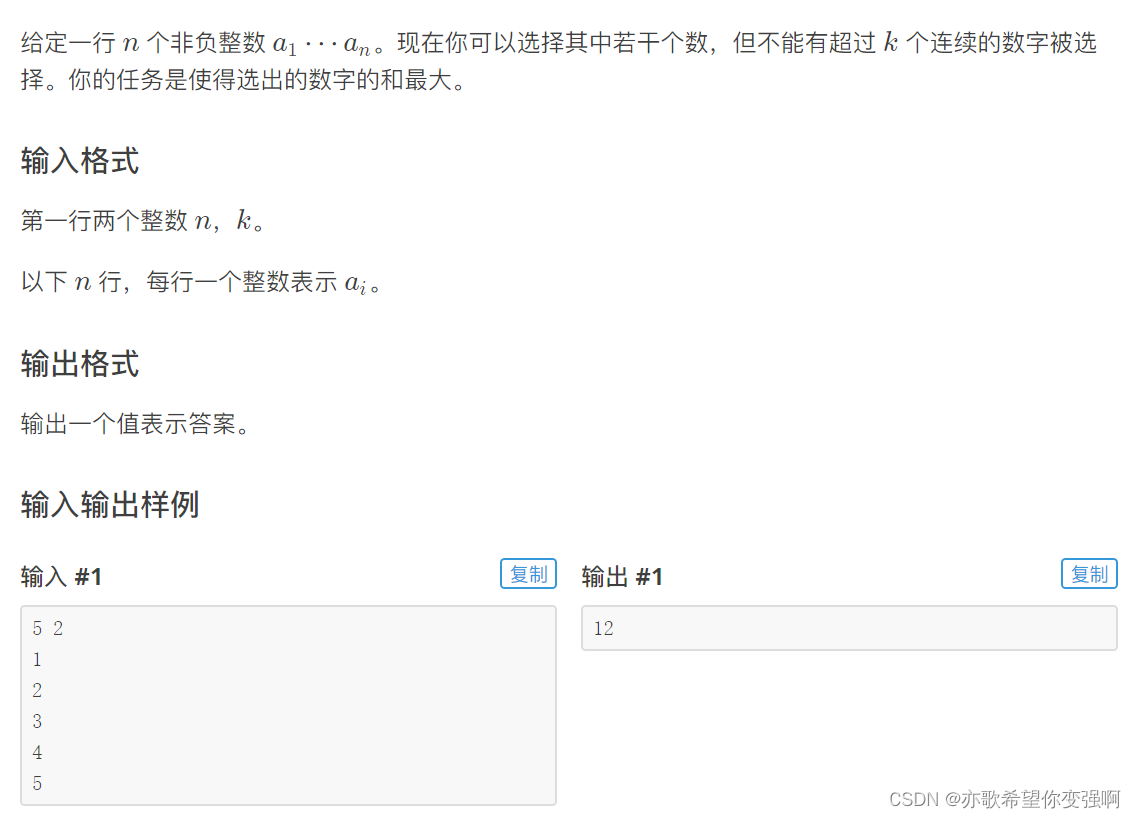

思路:
不同于连续的区间和,这个若干离散长度,且最大连续不超过k,和之前做法不一样。
每个点都有两种状态,被选上和未被选上,但是不能有连续超过k个被选上,那么不被选上的数应该会很少。
我们设置f[i] 代表第i个点不取的最优解。状态转移:f[i]=max{f[j],sum[j+1~i-1]}(i-j<=k)向后递推,最终求解f[n+1]即可(f[j]是不被选上的,故不能加上a[j])
那么如何判优呢?假设从f[a]转移到f[c]优于f[b]转移到f[c](a<b<c) 则f[a]+sum[c-1]-sum[a]>=f[b]+sum[c-1]-sum[b] 易得f[a]-sum[a]>=f[c]-sum[b]
故我们维护一个f[j]-sum[j]数组在[i-k-1~i-1]的单调队列,遍历每个i不断取出最大值即可
入队新元素为i-1 所以h<=t&&f[q[t]]-suf[q[t]]<f[i-1]-suf[i-1]
过期队头和i-k-1比较 所以h<=t&&q[h]<i-k-1 取等时成立
更新f[i] f[i]=f[q[h]]+suf[i-1]-suf[q[h]]
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int a[N],n,k,q[N];
ll suf[N],f[N];
int main(){
cin>>n>>k;
for(int i=1;i<=n;i++)cin>>a[i],suf[i]=suf[i-1]+a[i];
int h=1,t=0;
for(int i=1;i<=n+1;i++){
while(h<=t&&f[q[t]]-suf[q[t]]<f[i-1]-suf[i-1])t--;//这个一定要在最前面,因为这一步可能影响到q[h]
q[++t]=i-1;
while(h<=t&&q[h]<i-k-1)h++;
f[i]=f[q[h]]+suf[i-1]-suf[q[h]];
}
cout<<f[n+1];
}
题目:寻找段落

思路:
注意到段落长度是个范围(还很大),只能二分来做,那么是对段落长度二分吗? 这样的话怎么对获得的最大平均值来调整段落长度呢?
其实我们应该对最大平均值二分,然后根据题目的这个段落能不能达到,若能达到就继续减小最大平均值mid!!!
操作:首先对数组减去mid,那么只需要判断[s,t]的段落中有没有出现>=0,如果出现就说明答案至少是它,可以尝试增加mid
再细节一点:假如遍历到了i,那么只需要看看suf[i]-max(suf[i-T~i-S])有没有>=0,故我们要维护一个suf数组在[i-T, i-S]到最大值的单调队列,从而遍历所有i
入队新元素为i-S 所以h<=t&&suf[q[t]]>suf[i-S]
过期队头和i-T比较 所以h<=t&&q[h]<i-T 取等时也成立
判断suf[i]-suf[q[h]]>=0成不成立即可
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
double l,r,mid,a[N],suf[N];
int n,S,T,q[N];
int check(double mid){
int h=1,t=0;
suf[0]=0;
for(int i=1;i<=n;i++) suf[i]=suf[i-1]+a[i]-mid;//初始化前缀和数组
for(int i=S;i<=n;i++){
while(h<=t&&suf[q[t]]>suf[i-S])t--;//维护单调性,新元素为suf[i-S]哦
q[++t]=i-S;//入队
while(h<=t&&q[h]<i-T)h++;//过期的出队
if(h<=t&&suf[i]-suf[q[h]]>=0)return 1;//判断每个[S,T]长度的段落有没有>=0
}
return 0;
}
int main(){
cin>>n>>S>>T;
for(int i=1;i<=n;i++)cin>>a[i];
l=-100000,r=100000;
while(r-l>1e-5){//二分精确模板
mid=(l+r)/2;
if(check(mid))l=mid;
else r=mid;
}
printf("%.3f",mid);
}好了,讲完了,各位观众老爷们点个赞再走吧