目录
卷积
1 自定义二维卷积算子
2 自定义带步长和零填充的二维卷积算子
3 实现图像边缘检测
4 自定义卷积层算子和汇聚层算子
4.1 卷积算子
4.2 汇聚层算子
5 学习torch.nn.Conv2d()、torch.nn.MaxPool2d();torch.nn.avg_pool2d(),简要介绍使用方法。
6 分别用自定义卷积算子和torch.nn.Conv2d()编程实现下面的卷积运算
总结
卷积
考虑到使用全连接前馈网络来处理图像时,会出现如下问题:
1. 模型参数过多,容易发生过拟合。在全连接前馈网络中,隐藏层的每个神经元都要跟该层所有输入的神经元相连接。随着隐藏层神经元数量的增多,参数的规模也会急剧增加,导致整个神经网络的训练效率非常低,也很容易发生过拟合。
2. 难以提取图像中的局部不变性特征。 自然图像中的物体都具有局部不变性特征,比如尺度缩放、平移、旋转等操作不影响其语义信息。而全连接前馈网络很难提取这些局部不变性特征。
卷积神经网络有三个结构上的特性:局部连接、权重共享和汇聚。这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性。和前馈神经网络相比,卷积神经网络的参数也更少。因此,通常会使用卷积神经网络来处理图像信息。
卷积是分析数学中的一种重要运算,常用于信号处理或图像处理任务。本节以二维卷积为例来进行实践。
1 自定义二维卷积算子
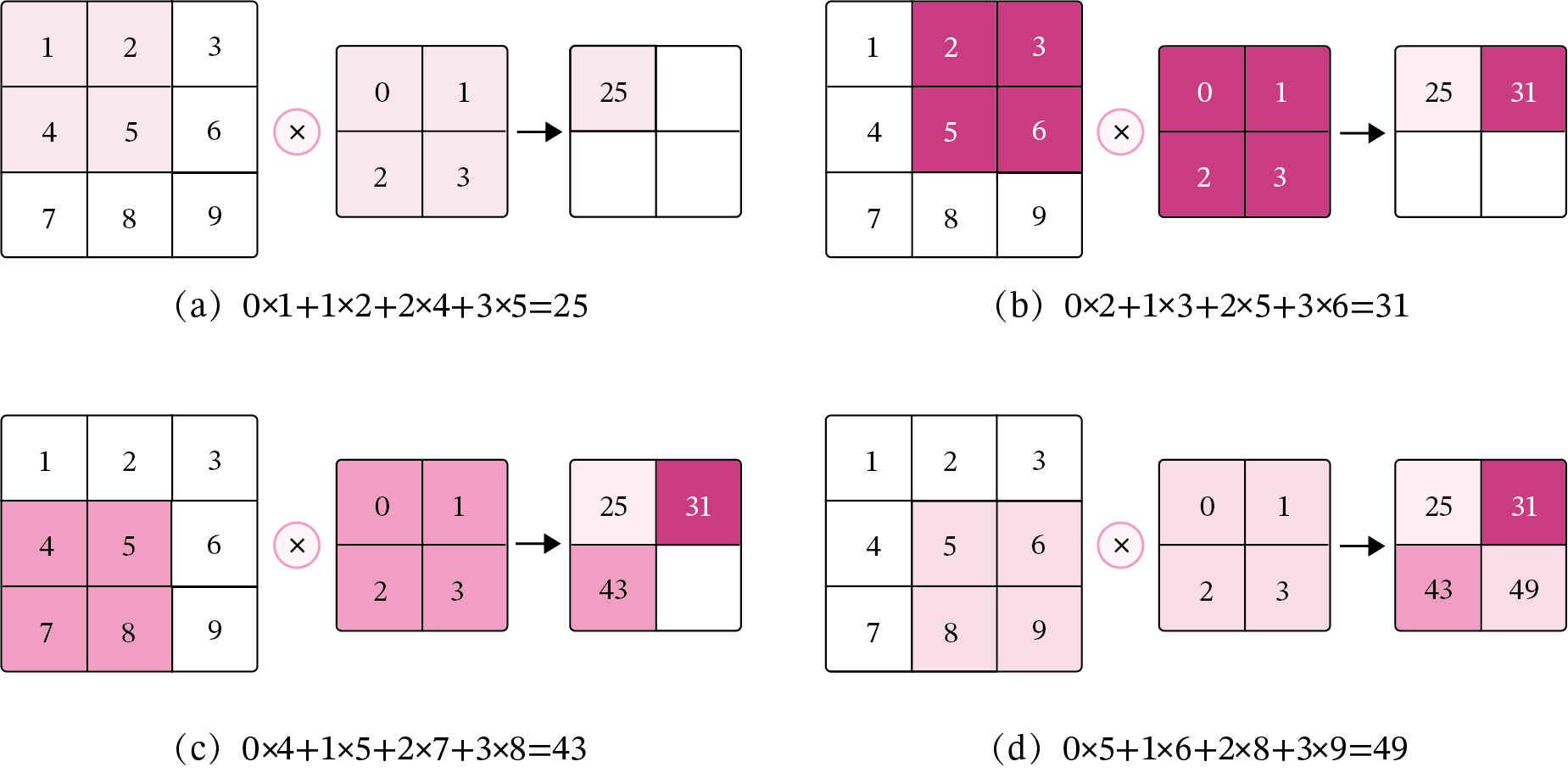
在机器学习和图像处理领域,卷积的主要功能是在一个图像(或特征图)上滑动一个卷积核,通过卷积操作得到一组新的特征。在计算卷积的过程中,需要进行卷积核的翻转,而这也会带来一些不必要的操作和开销。因此,在具体实现上,一般会以数学中的互相关(Cross-Correlatio)运算来代替卷积。
在神经网络中,卷积运算的主要作用是抽取特征,卷积核是否进行翻转并不会影响其特征抽取的能力。特别是当卷积核是可学习的参数时,卷积和互相关在能力上是等价的。因此,很多时候,为方便起见,会直接用互相关来代替卷积。
在本案例之后的描述中,除非特别声明,卷积一般指“互相关”。
对于一个输入矩阵![]() 和一个滤波器
和一个滤波器![]() ,他们的卷积为:
,他们的卷积为:
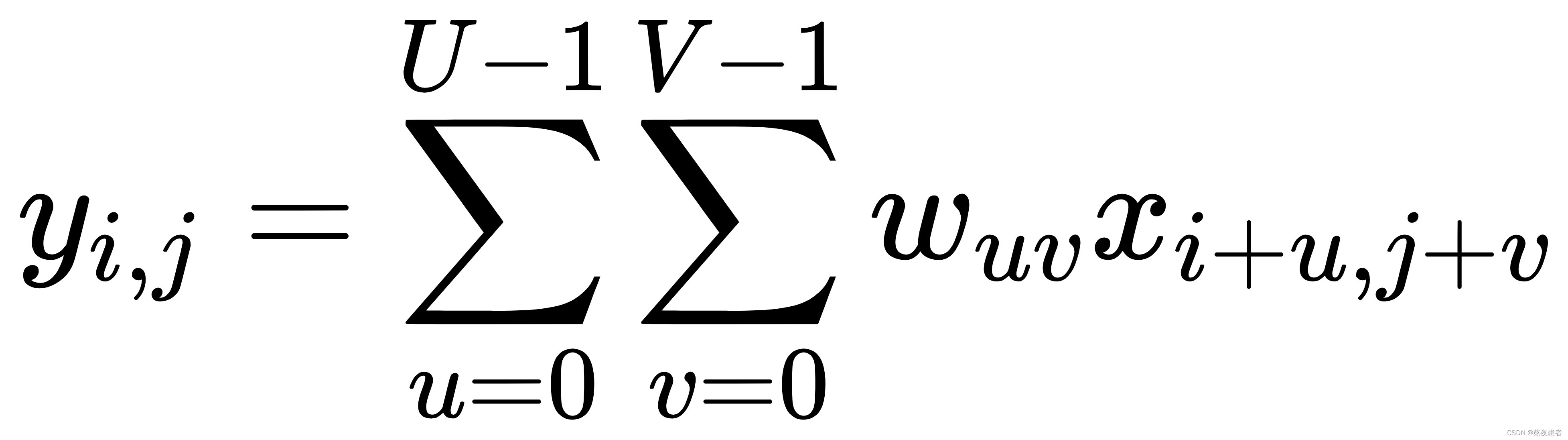
此时图片的输出大小为:
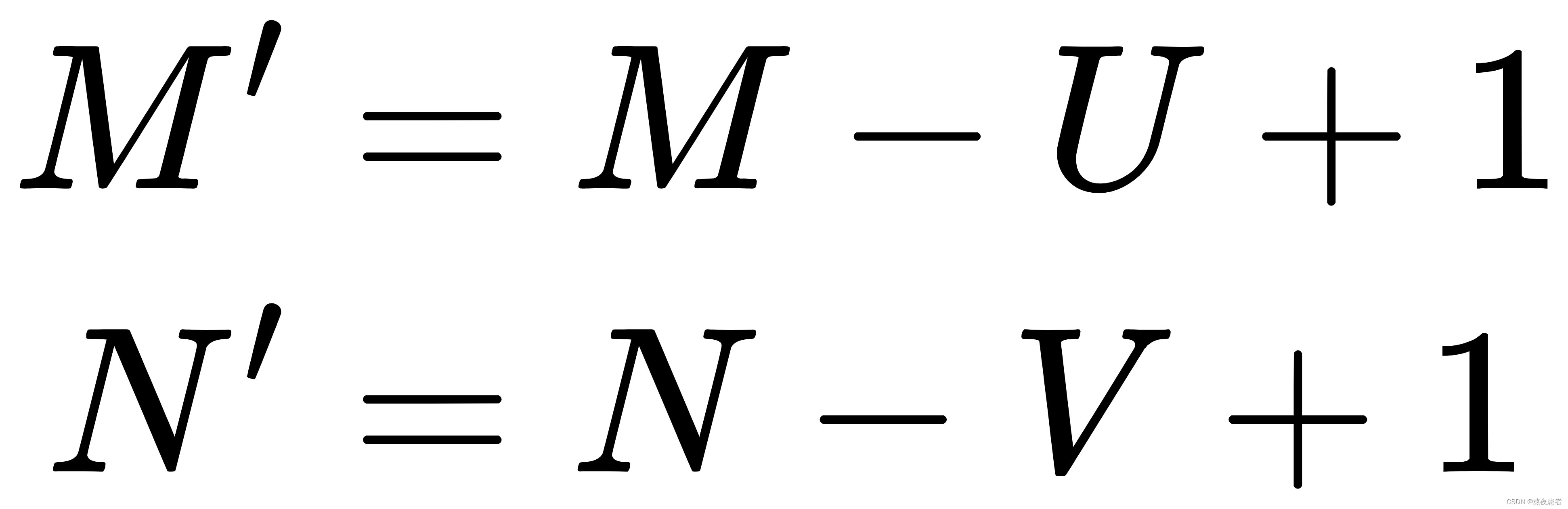
计算量为:
![]()
import torch
import numpy as np
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, kernel_size, stride=1, padding=0, ):
super(Conv2D, self).__init__()
w = torch.tensor(np.array([[0., 1.], [2., 3.]], dtype='float32').reshape([kernel_size, kernel_size]))
self.weight = torch.nn.Parameter(w, requires_grad=True)
def forward(self, X):
"""
输入:
- X:输入矩阵,shape=[B, M, N],B为样本数量
输出:
- output:输出矩阵
"""
u, v = self.weight.shape
output = torch.zeros([X.shape[0], X.shape[1] - u + 1, X.shape[2] - v + 1])
for i in range(output.shape[1]):
for j in range(output.shape[2]):
output[:, i, j] = torch.sum(X[:, i:i + u, j:j + v] * self.weight, dim=[1, 2])
return output
# 随机构造一个二维输入矩阵
inputs = torch.tensor([[[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]])
conv2d = Conv2D(kernel_size=2)
outputs = conv2d(inputs)
print("input: {}, \noutput: {}".format(inputs, outputs))

2 自定义带步长和零填充的二维卷积算子
在计算卷积时,可以在所有维度上每间隔个元素计算一次,
称为卷积运算的步长(Stride),也就是卷积核在滑动时的间隔。
在二维卷积运算中,零填充(Zero Padding)是指在输入矩阵周围对称地补上个
。
对于一个输入矩阵和一个滤波器
,,步长为
,对输入矩阵进行零填充,那么最终输出矩阵大小则为

计算量为:
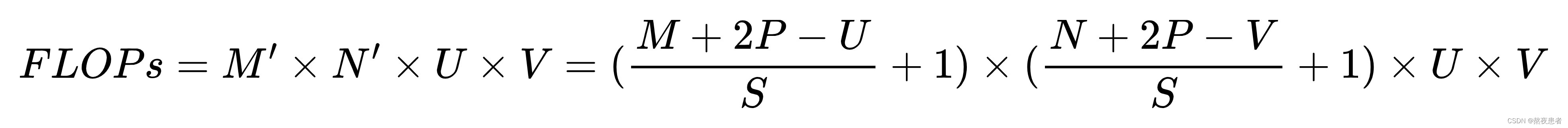
一般常用的卷积有三种:
1. 窄卷积:步长,两端不补零
,卷积后输出尺寸为:
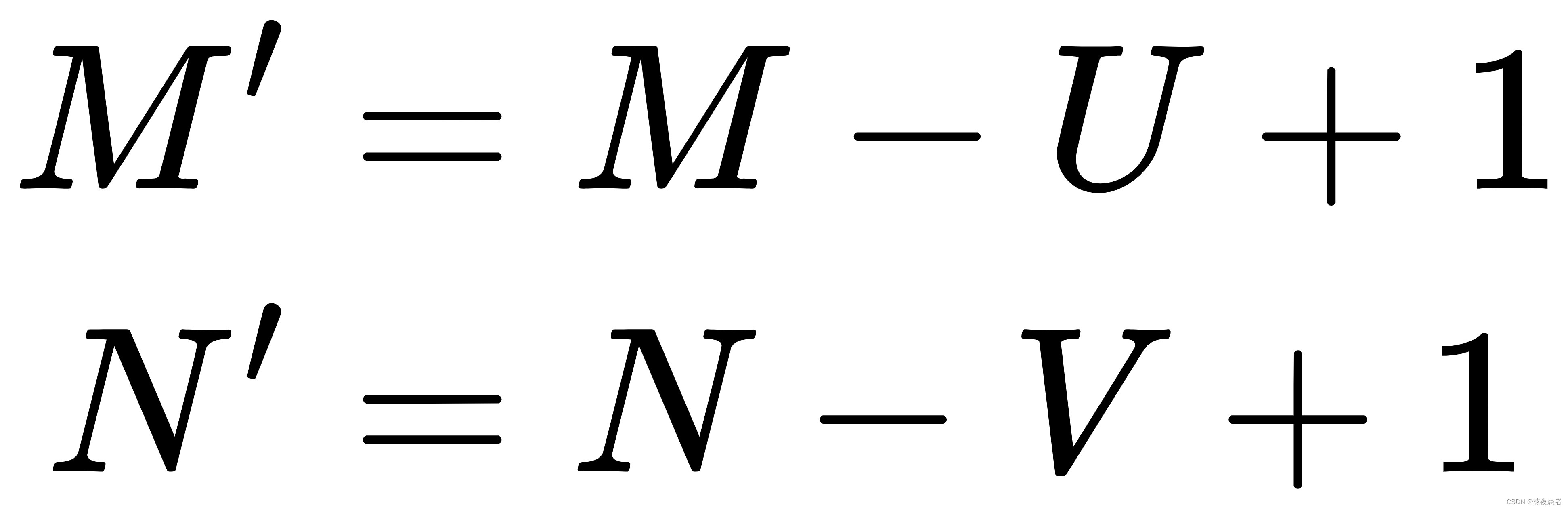
2. 宽卷积:步长,两端补零
,卷积后输出尺寸为:
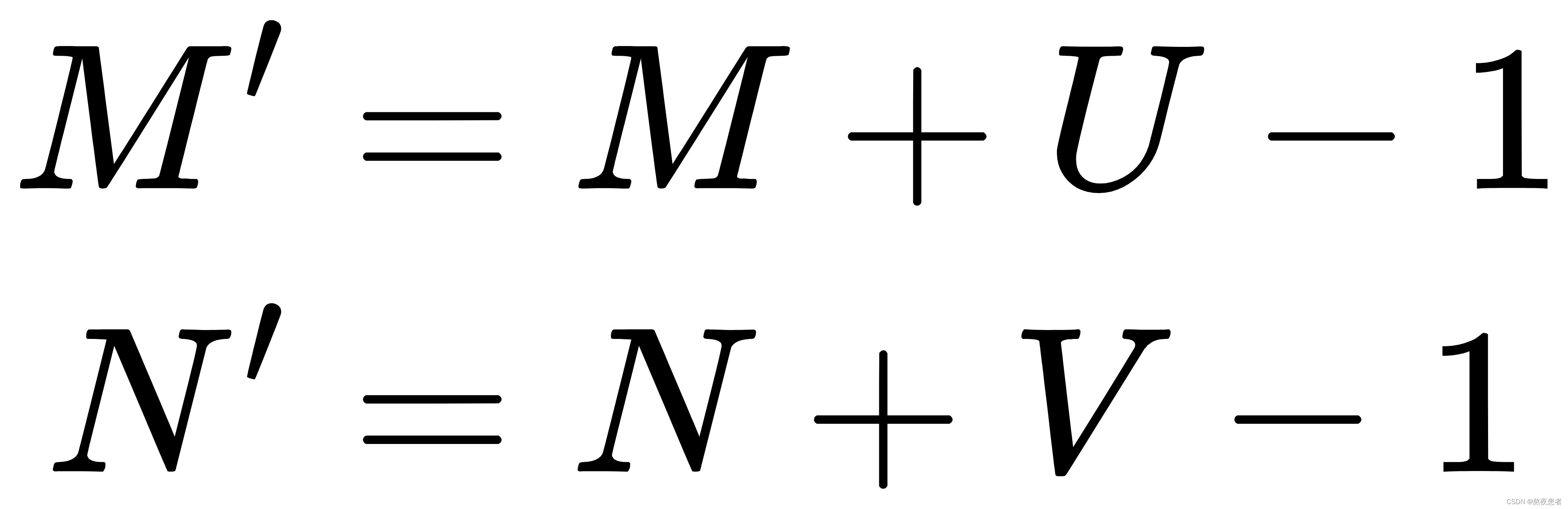
3. 等宽卷积:步长,两端补零
,卷积后输出尺寸为:

import torch
import numpy as np
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, kernel_size, stride=1, padding=0, ):
super(Conv2D, self).__init__()
w = torch.tensor(np.array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.]], dtype='float32').reshape([kernel_size, kernel_size]))
self.weight = torch.nn.Parameter(w, requires_grad=True)
# 步长
self.stride = stride
# 零填充
self.padding = padding
def forward(self, X):
"""
输入:
- X:输入矩阵,shape=[B, M, N],B为样本数量
输出:
- output:输出矩阵
"""
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding]) # 创建一个M'*N'的零矩阵
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X # 将原数据放回
u, v = self.weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * self.weight,
dim=[1, 2])
return output
# 随机构造一个二维输入矩阵
inputs = torch.randn([2, 8, 8])
conv2d_padding = Conv2D(kernel_size=3, padding=1)
outputs = conv2d_padding(inputs)
print("When kernel_size=3, padding=1 stride=1, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))
conv2d_stride = Conv2D(kernel_size=3, stride=2, padding=1)
outputs = conv2d_stride(inputs)
print("When kernel_size=3, padding=1 stride=2, input's shape: {}, output's shape: {}".format(inputs.shape, outputs.shape))

从输出结果看出,使用大小卷积,padding为1,当stride=1时,模型的输出特征图可以与输入特征图保持一致;当stride=2时,输出特征图的宽和高都缩小一倍。
3 实现图像边缘检测
在图像处理任务中,常用拉普拉斯算子对物体边缘进行提取,拉普拉斯算子为一个大小为的卷积核,中心元素值是
,其余元素值是
。
考虑到边缘其实就是图像上像素值变化很大的点的集合,因此可以通过计算二阶微分得到,当二阶微分为0时,像素值的变化最大。此时,对方向和
方向分别求取二阶导数:
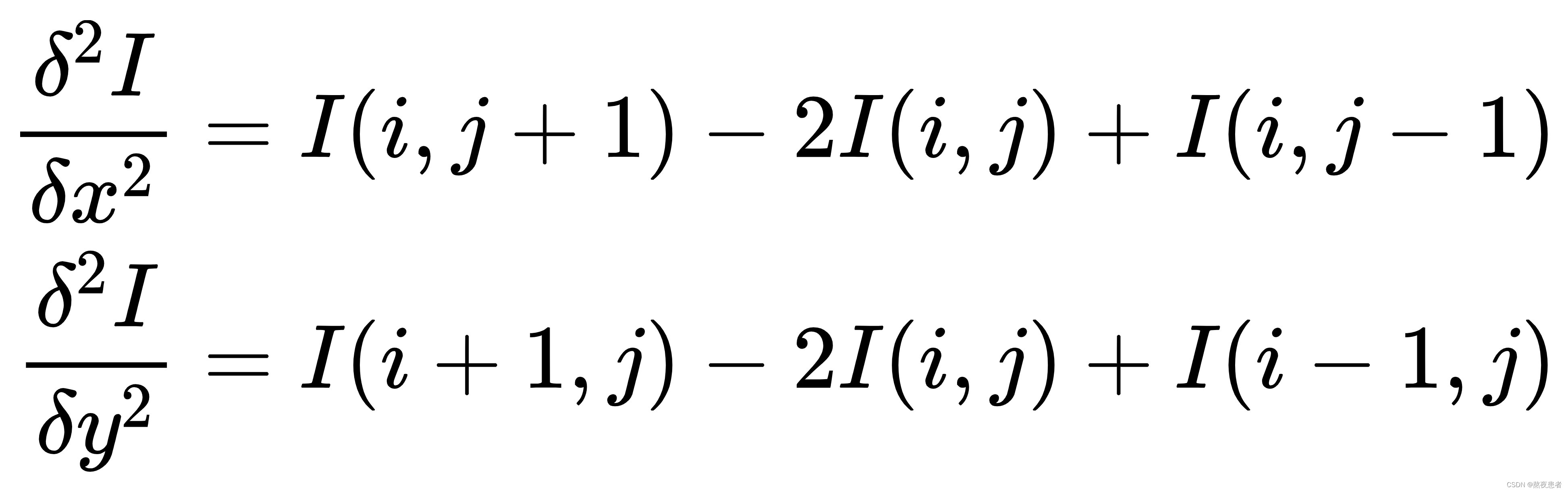
完整的二阶微分公式为:
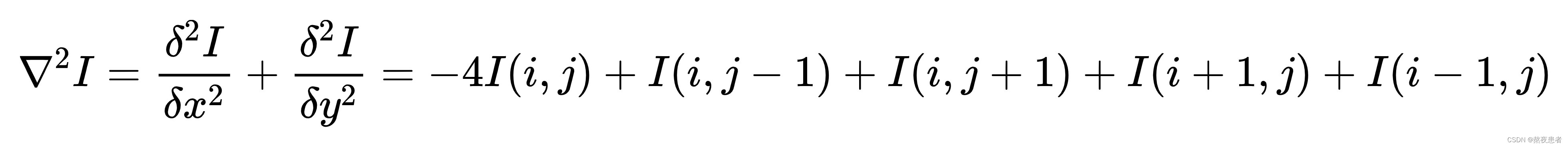
上述公式也被称为拉普拉斯算子,对应的二阶微分卷积核为:
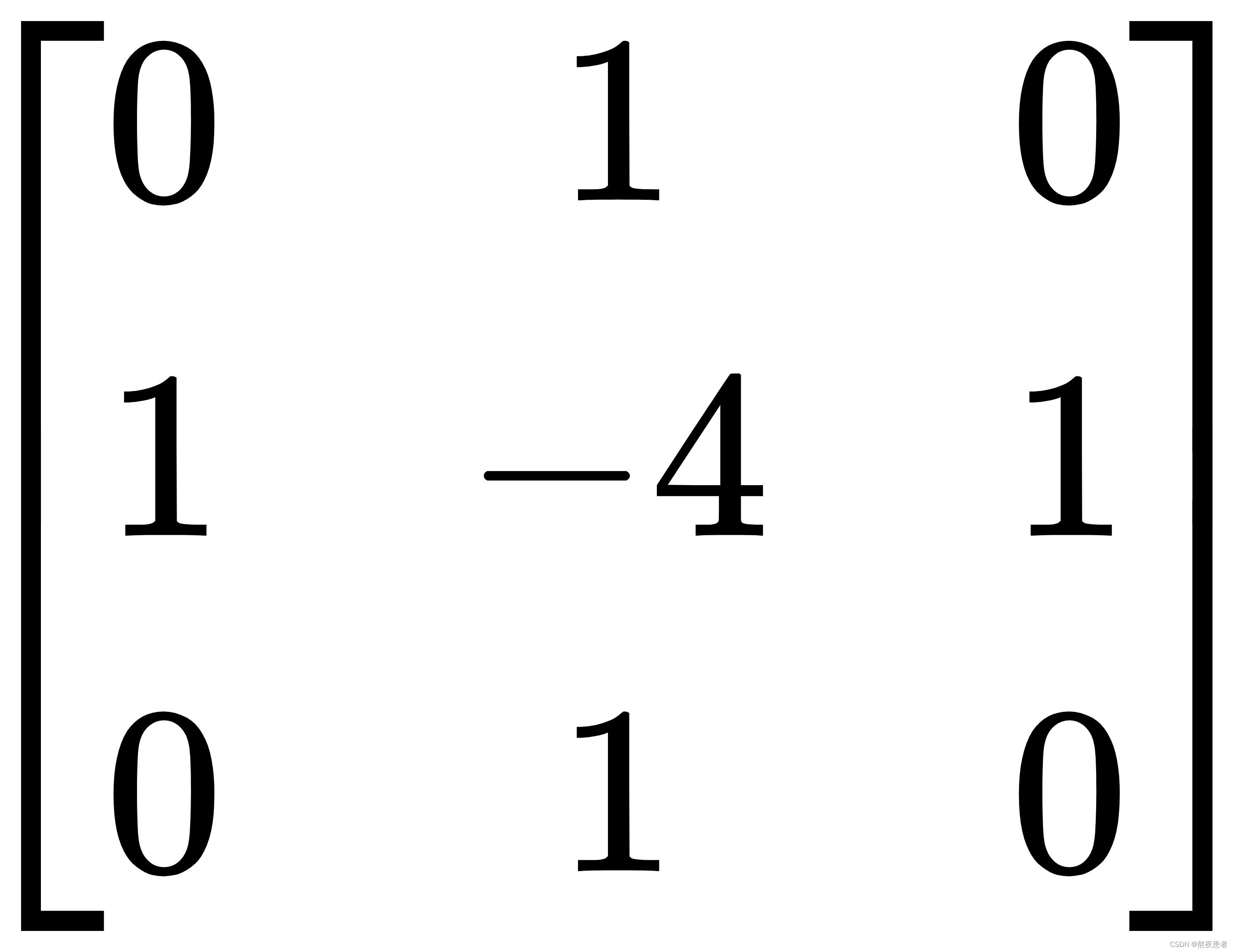
对上述算子全部求反也可以起到相同的作用,此时,该算子可以表示为:
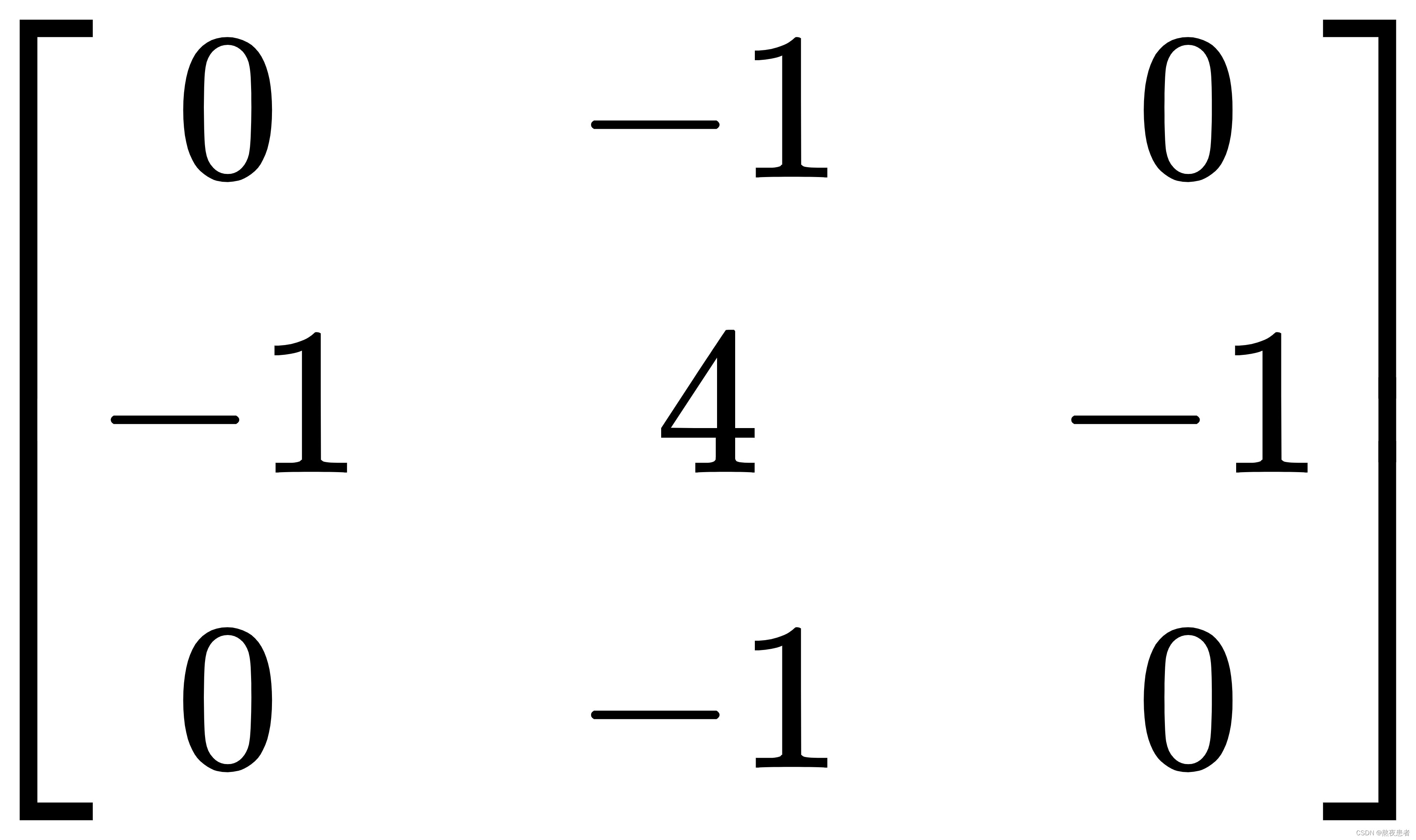
也就是一个点的四邻域拉普拉斯的算子计算结果是自己像素值的四倍减去上下左右的像素的和,将这个算子旋转后与原算子相加,就变成八邻域的拉普拉斯算子,也就是一个像素自己值的八倍减去周围一圈八个像素值的和,做为拉普拉斯计算结果,此时,该算子可以表示为:

代码如下:
import torch
import matplotlib.pyplot as plt
from PIL import Image
import numpy as np
import torch.nn as nn
class Conv2d(nn.Module):
def __init__(self, kernel_size, stride=1, padding=0):
super(Conv2d, self).__init__()
# 设置卷积核参数
w = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32').reshape((3, 3))
w = torch.from_numpy(w)
self.weight = torch.nn.Parameter(w, requires_grad=True)
self.stride = stride
self.padding = padding
def forward(self, X):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
u, v = self.weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * self.weight,
dim=[1, 2])
return output
# 读取图片
img = Image.open('OIP-C.jpg').convert('L')
inputs = np.array(img, dtype='float32')
# 创建卷积算子,卷积核大小为3x3,并使用上面的设置好的数值作为卷积核权重的初始化参数
conv = Conv2d(kernel_size=3, stride=1, padding=0)
print("bf to_tensor, inputs:", inputs)
# 将图片转为Tensor
inputs = torch.tensor(inputs)
print("bf unsqueeze, inputs:", inputs)
inputs = torch.unsqueeze(inputs, dim=0)
print("af unsqueeze, inputs:", inputs)
outputs = conv(inputs)
print(outputs)
# 可视化结果
plt.figure(figsize=(8, 4))
f = plt.subplot(121)
f.set_title('input image', fontsize=15)
plt.imshow(img)
f = plt.subplot(122)
f.set_title('output feature map', fontsize=15)
plt.imshow(outputs.squeeze().detach().numpy(), cmap='gray')
plt.show()

4 自定义卷积层算子和汇聚层算子
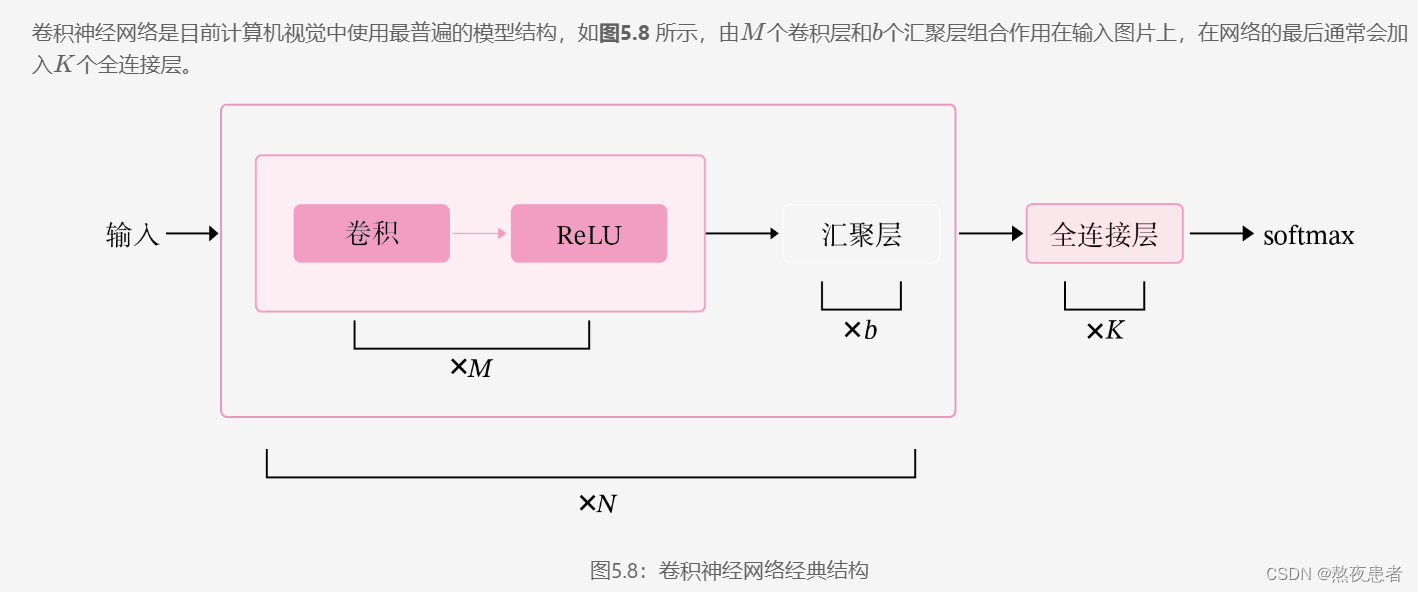
从上图可以看出,卷积网络是由多个基础的算子组合而成。下面我们先实现卷积网络的两个基础算子:卷积层算子和汇聚层算子。
4.1 卷积算子
卷积层是指用卷积操作来实现神经网络中一层。为了提取不同种类的特征,通常会使用多个卷积核一起进行特征提取。
在前面介绍的二维卷积运算中,卷积的输入数据是二维矩阵。但实际应用中,一幅大小为的图片中的每个像素的特征表示不仅仅只有灰度值的标量,通常有多个特征,可以表示为
维的向量,比如RGB三个通道的特征向量。因此,图像上的卷积操作的输入数据通常是一个三维张量,分别对应了图片的高度
、宽度
和深度
,其中深度
通常也被称为输入通道数
。如果输入如果是灰度图像,则输入通道数为1;如果输入是彩色图像,分别有
三个通道,则输入通道数为3。
此外,由于具有单个核的卷积每次只能提取一种类型的特征,即输出一张大小为的特征图(Feature Map)。而在实际应用中,我们也希望每一个卷积层能够提取多种不同类型的特征,所以一个卷积层通常会组合多个不同的卷积核来提取特征,经过卷积运算后会输出多张特征图,不同的特征图对应不同类型的特征。输出特征图的个数通常将其称为输出通道数
。
PS:假设一个卷积层的输入特征图,其中
为特征图的尺寸,
代表通道数;卷积核为
,其中
为卷积核的尺寸,
代表输入通道数,
代表输出通道数。

多张输出特征图的计算,如下图所示,具体的对这个不明确的可以翻翻我之前的博客,对这个解释的比较详细.
class Conv2D(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
super(Conv2D, self).__init__()
# 创建卷积核
weight = torch.zeros([out_channels, in_channels, kernel_size, kernel_size], dtype=torch.float32)
weight = nn.init.constant_(weight, val=1.0)
self.weight = nn.Parameter(weight)
# 创建偏置
bias = torch.zeros([out_channels, 1], dtype=torch.float32)
self.bias = nn.init.constant_(bias, val=0.0) # 值可调整
self.bias = nn.Parameter(bias)
# 步长
self.stride = stride
# 零填充
self.padding = padding
# 输入通道数
self.in_channels = in_channels
# 输出通道数
self.out_channels = out_channels
def single_forward(self, X, weight):
"""
输入:
- X:输入矩阵,shape=[B, M, N],B为样本数量
输出:
- output:输出矩阵
"""
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding]) # 创建一个M'*N'的零矩阵
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X # 将原数据放回
u, v = weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * weight,
dim=[1, 2])
return output
def forward(self, inputs):
"""
输入:
- inputs:输入矩阵,shape=[B, D, M, N]
- weights:P组二维卷积核,shape=[P, D, U, V]
- bias:P个偏置,shape=[P, 1]
"""
feature_maps = []
# 进行多次多输入通道卷积运算
p = 0
for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
multi_outs = []
# 循环计算每个输入特征图对应的卷积结果
for i in range(self.in_channels):
single = self.single_forward(inputs[:, i, :, :], w[i])
multi_outs.append(single)
# print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
# 将所有卷积结果相加
feature_map = torch.sum(torch.stack(multi_outs), dim=0) + b # Zp
feature_maps.append(feature_map)
# print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
p += 1
# 将所有Zp进行堆叠
out = torch.stack(feature_maps, 1)
return out

4.2 汇聚层算子
汇聚层的作用是进行特征选择,降低特征数量,从而减少参数数量。由于汇聚之后特征图会变得更小,如果后面连接的是全连接层,可以有效地减小神经元的个数,节省存储空间并提高计算效率。
常用的汇聚方法有两种,分别是:平均汇聚和最大汇聚。
- 平均汇聚:将输入特征图划分为
大小的区域,对每个区域内的神经元活性值取平均值作为这个区域的表示;
- 最大汇聚:使用输入特征图的每个子区域内所有神经元的最大活性值作为这个区域的表示。
 汇聚层输出的计算尺寸与卷积层一致,对于一个输入矩阵
汇聚层输出的计算尺寸与卷积层一致,对于一个输入矩阵和一个运算区域大小为
的汇聚层,步长为
,对输入矩阵进行零填充,那么最终输出矩阵大小则为

由于过大的采样区域会急剧减少神经元的数量,也会造成过多的信息丢失。目前,在卷积神经网络中比较典型的汇聚层是将每个输入特征图划分为大小的不重叠区域,然后使用最大汇聚的方式进行下采样。
由于汇聚是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出,所以其好处是当输入数据做出少量平移时,经过汇聚运算后的大多数输出还能保持不变。比如:当识别一张图像是否是人脸时,我们需要知道人脸左边有一只眼睛,右边也有一只眼睛,而不需要知道眼睛的精确位置,这时候通过汇聚某一片区域的像素点来得到总体统计特征会显得很有用。这也就体现了汇聚层的平移不变特性。
汇聚层的参数量和计算量
由于汇聚层中没有参数,所以参数量为;最大汇聚中,没有乘加运算,所以计算量为
,而平均汇聚中,输出特征图上每个点都对应了一次求平均运算.
class Pool2D(nn.Module):
def __init__(self, size=(2, 2), mode='max', stride=1):
super(Pool2D, self).__init__()
# 汇聚方式
self.mode = mode
self.h, self.w = size
self.stride = stride
def forward(self, x):
output_w = (x.shape[2] - self.w) // self.stride + 1
output_h = (x.shape[3] - self.h) // self.stride + 1
output = torch.zeros([x.shape[0], x.shape[1], output_w, output_h])
# 汇聚
for i in range(output.shape[2]):
for j in range(output.shape[3]):
# 最大汇聚
if self.mode == 'max':
value_m = max(torch.max(
x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h],
dim=3).values[0][0])
output[:, :, i, j] = torch.tensor(value_m)
# 平均汇聚
elif self.mode == 'avg':
output[:, :, i, j] = torch.mean(
x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h],
dim=[2, 3])
return output
inputs = torch.tensor([[[[1., 2., 3., 4.], [5., 6., 7., 8.], [9., 10., 11., 12.], [13., 14., 15., 16.]]]])
pool2d = Pool2D(stride=2)
outputs = pool2d(inputs)
print("input: {}, \noutput: {}".format(inputs.shape, outputs.shape))
# 比较Maxpool2D与paddle API运算结果
maxpool2d_torch = nn.MaxPool2d(kernel_size=(2, 2), stride=2)
outputs_torch = maxpool2d_torch(inputs)
# 自定义算子运算结果
print('Maxpool2D outputs:', outputs)
# paddle API运算结果
print('nn.Maxpool2D outputs:', outputs_torch)
# 比较Avgpool2D与torch API运算结果
avgpool2d_torch = nn.AvgPool2d(kernel_size=(2, 2), stride=2)
outputs_torch = avgpool2d_torch(inputs)
pool2d = Pool2D(mode='avg', stride=2)
outputs = pool2d(inputs)
# 自定义算子运算结果
print('Avgpool2D outputs:', outputs)
# paddle API运算结果
print('nn.Avgpool2D outputs:', outputs_torch)
5 学习torch.nn.Conv2d()、torch.nn.MaxPool2d();torch.nn.avg_pool2d(),简要介绍使用方法。
torch.nn.Conv2d()参数如下:

torch.nn.MaxPool2d()参数如下:

torch.nn.AvgPool2d()参数如下:

具体的使用可以参照卷积层算子和池化层算子的代码中,有将调用库函数做比较~
6 分别用自定义卷积算子和torch.nn.Conv2d()编程实现下面的卷积运算
import torch.nn as nn
import torch
class Conv2D(nn.Module):
def __init__(self, in_channels, Kernel, out_channels, kernel_size, stride=1, padding=0):
super(Conv2D, self).__init__()
self.weight = nn.Parameter(Kernel)
# 创建偏置
self.bias = nn.Parameter(torch.tensor([1, 0], dtype=torch.float32))
# 步长
self.stride = stride
# 零填充
self.padding = padding
# 输入通道数
self.in_channels = in_channels
# 输出通道数
self.out_channels = out_channels
def single_forward(self, X, weight):
"""
输入:
- X:输入矩阵,shape=[B, M, N],B为样本数量
输出:
- output:输出矩阵
"""
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding]) # 创建一个M'*N'的零矩阵
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X # 将原数据放回
u, v = weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * weight,
dim=[1, 2])
return output
def forward(self, inputs):
"""
输入:
- inputs:输入矩阵,shape=[B, D, M, N]
- weights:P组二维卷积核,shape=[P, D, U, V]
- bias:P个偏置,shape=[P, 1]
"""
feature_maps = []
# 进行多次多输入通道卷积运算
p = 0
for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
multi_outs = []
# 循环计算每个输入特征图对应的卷积结果
for i in range(self.in_channels):
single = self.single_forward(inputs[:, i, :, :], w[i])
multi_outs.append(single)
# print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
# 将所有卷积结果相加
feature_map = torch.sum(torch.stack(multi_outs), dim=0) + b # Zp
feature_maps.append(feature_map)
# print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
p += 1
# 将所有Zp进行堆叠
out = torch.stack(feature_maps, 1)
return out
x = torch.tensor([
[[0, 1, 1, 0, 2],
[2, 2, 2, 2, 1],
[1, 0, 0, 2, 0],
[0, 1, 1, 0, 0],
[1, 2, 0, 0, 2]],
[[1, 0, 2, 2, 0],
[0, 0, 0, 2, 0],
[1, 2, 1, 2, 1],
[1, 0, 0, 0, 0],
[1, 2, 1, 1, 1]],
[[2, 1, 2, 0, 0],
[1, 0, 0, 1, 0],
[0, 2, 1, 0, 1],
[0, 1, 2, 2, 2],
[2, 1, 0, 0, 1]]], dtype=torch.float32).reshape([1, 3, 5, 5])
Kernel = torch.tensor([
[[[-1, 1, 0],
[0, 1, 0],
[0, 1, 1]],
[[-1, -1, 0],
[0, 0, 0],
[0, -1, 0]],
[[0, 0, -1],
[0, 1, 0],
[1, -1, -1]]],
[[[1, 1, -1],
[-1, -1, 1],
[0, -1, 1]],
[[0, 1, 0],
[-1, 0, -1],
[-1, 1, 0]],
[[-1, 0, 0],
[-1, 0, 1],
[-1, 0, 0]]]], dtype=torch.float32).reshape([2, 3, 3, 3])
conv2d = Conv2D(in_channels=3, Kernel=Kernel, out_channels=2, kernel_size=3, padding=1, stride=2)
print("inputs shape:",x.shape)
outputs = conv2d(x)
print("Conv2D outputs shape:",outputs.shape)
print(outputs)
conv2d_2 = nn.Conv2d(in_channels=3, out_channels=2, kernel_size=3, padding=1, stride=(2, 2), bias=True)
conv2d_2.weight = torch.nn.Parameter(Kernel)
conv2d_2.bias = torch.nn.Parameter(torch.tensor([1, 0], dtype=torch.float32))
out = conv2d_2(x)
print(out)
运行结果如下:
 好了到这儿,最蒙圈的地方来了,下面是老师给的图,但是怎么算这也不对啊
好了到这儿,最蒙圈的地方来了,下面是老师给的图,但是怎么算这也不对啊
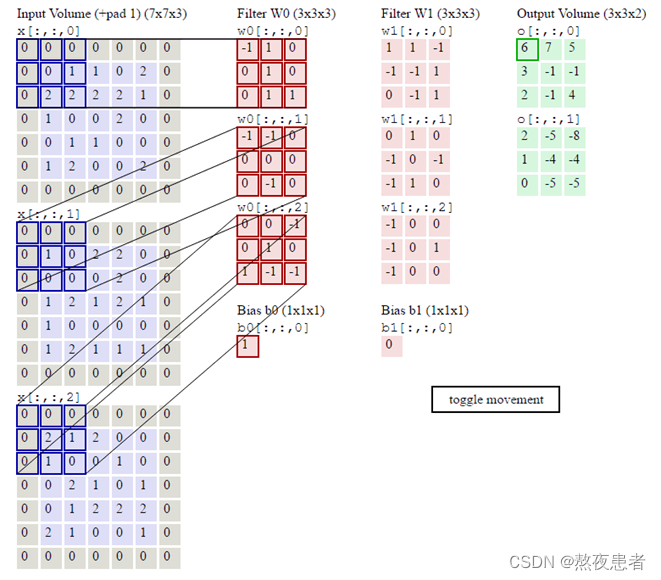
总结
本次实验较为有难度,通过再次对池化层、卷积层,手推和调用库函数的代码的整理书写,对整个流程也更为明确了,就最后一个实践的时候有一点点困难,对于变量初始化、传入值的维度还是不明确这里总结一下。
对于卷积层的输入x:[batch_size(样本数), in_channel(图片的通道数), H, W(分别代表宽高)]
卷积核w:[out_channel(输出通道,输出需要有几个通道), in_channel(输入通道数,图片有几个通道, H, W(卷积核的宽高)]
偏置b:[1, out_channel(输出通道数)]