题目
647. 回文子串
中等
相关标签
字符串 动态规划
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc" 输出:3 解释:三个回文子串: "a", "b", "c"
示例 2:
输入:s = "aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示:
1 <= s.length <= 1000s由小写英文字母组成
思路和解题方法 一 动态规划
vector<vector<bool>> dp(s.size(),vector<bool>(s.size(),false));:这行代码定义了一个二维布尔类型的动态规划数组dp,用来记录字符串s中从位置i到j的子串是否为回文串。
int ans = 0;:初始化一个变量ans用来存储回文子串的数量。
for(int i = s.size()-1;i>=0;i--):从字符串的末尾向前遍历每个字符,作为子串的起始位置。
for(int j = i;j<s.size();j++):遍历以当前i位置字符为起始的所有可能的子串。
if(s[i] == s[j] && (j-i<=1||dp[i+1][j-1])):如果当前子串的两端字符相同,并且长度不超过1,或者去掉两端字符后剩下的子串是回文串(根据dp数组的记录),则认为当前子串是回文串。
ans++;:累加回文子串的数量。
dp[i][j] = true;:更新dp数组,表示从位置i到j的子串是回文串。最后返回ans,即为字符串s中回文子串的数量。
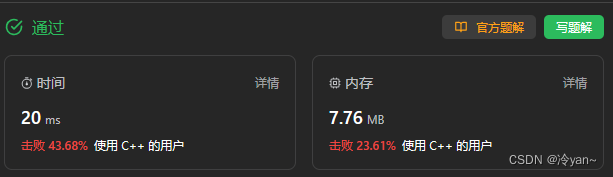
复杂度
时间复杂度:
O(n*n)
时间复杂度为O(n^2),其中n为输入字符串s的长度。这是因为代码中使用了两重循环来遍历所有可能的子串,并在每次循环中进行常数时间的比较和更新操作。
空间复杂度
O(n*n)
至于空间复杂度,由于使用了一个二维动态规划数组dp,其大小为s.size() * s.size(),因此空间复杂度也为O(n^2)。
c++ 代码 1
打印的dp数组:(以“abcba"为样例)
a b c b a

class Solution {
public:
int countSubstrings(string s) {
// 创建一个二维动态规划数组dp,用于记录子串是否为回文
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
int ans = 0; // 记录回文子串的数量
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i; j < s.size(); j++) {
// 如果当前字符相等,并且满足回文条件,则更新结果和dp数组
if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
ans++; // 回文子串数量加一
dp[i][j] = true; // 更新dp数组表示从i到j的子串是回文
}
}
}
return ans; // 返回回文子串的数量
}
};
双指针
先看时间空间复杂度对比:(大差不差的区别)
以下是双指针法
思路和解题方法 二 双指针
主函数
countSubstrings中,首先初始化变量ans为0,用于存储回文子串的数量。然后通过一个for循环遍历字符串
s的每个字符(下标为i),对于每个字符,分别调用explore函数两次:
- 第一次调用
explore(s, i, i, s.size()):以当前字符为中心,向两边扩展寻找回文子串。- 第二次调用
explore(s, i, i+1, s.size()):以当前字符和下一个字符为中心,向两边扩展寻找回文子串。在
explore函数中,通过双指针i和j向两边扩展,检查以i和j为中心的回文子串数量。当i和j位置的字符相等时,i向左移动,j向右移动,并同时增加回文子串数量
cnt。最后返回
cnt作为以i和j为中心的回文子串数量。最后,主函数返回累加的回文子串数量
ans。
复杂度
时间复杂度:
O(n*n)
时间复杂度为O(n^2),其中n为输入字符串s的长度。这是因为在主函数
countSubstrings中,通过一个嵌套的循环遍历字符串s的每个字符,并且在explore函数中,利用双指针向两边扩展来判断回文子串,最坏情况下需要O(n)的时间复杂度。
空间复杂度
O(1)
空间复杂度则为O(1),因为除了存储回文子串数量的变量
ans外,算法并未使用额外的空间,因此空间复杂度是常数级的。
c++ 代码 2
class Solution {
public:
int countSubstrings(string s) {
int ans = 0; // 初始化回文子串数量为0
for(int i = 0; i < s.size(); i++) { // 遍历字符串s的每个字符
ans += explore(s, i, i, s.size()); // 以当前字符为中心,向两边扩展寻找回文子串
ans += explore(s, i, i + 1, s.size()); // 以当前字符和下一个字符为中心,向两边扩展寻找回文子串
}
return ans; // 返回回文子串的总数量
}
int explore(const string &s, int i, int j, int n) {
int cnt = 0; // 记录以i和j为中心的回文子串数量
while(i >= 0 && j < n && s[i] == s[j]) { // 向两边扩展,直到不是回文串为止
i--; // 向左移动指针
j++; // 向右移动指针
cnt++; // 回文子串数量加一
}
return cnt; // 返回回文子串数量
}
};
附Java代码
1.动态规划
class Solution {
public int countSubstrings(String s) {
// 创建一个二维数组dp,dp[i][j]表示从索引i到索引j的子串是否为回文子串
boolean[][] dp = new boolean[s.length()][s.length()];
int res = 0; // 用于存储回文子串数量的变量
// 双重循环遍历字符串,i表示起始索引,j表示结束索引
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
// 如果当前字符相等,并且满足以下条件之一:
// 1. j和i相差不超过1,即长度为1或2的子串
// 2. dp[i+1][j-1]为true,即去掉头尾字符后的子串是回文串
if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {
res++; // 回文子串数量加1
dp[i][j] = true; // 标记索引i到索引j的子串为回文子串
}
}
}
return res; // 返回回文子串数量
}
}
2.双指针
class Solution {
public int countSubstrings(String s) {
int len, ans = 0; // 初始化变量len和ans
if (s == null || (len = s.length()) < 1) return 0; // 如果输入字符串为空或长度小于1,则直接返回0
// 总共有2 * len - 1个中心点,因为可以以每个字符为中心,也可以以两个字符之间的空隙为中心
for (int i = 0; i < 2 * len - 1; i++) {
// 通过遍历每个回文中心,向两边扩散,并判断是否回文子串
// 有两种情况,当i为偶数时,回文中心是一个字符;当i为奇数时,回文中心是两个字符之间的空隙
int left = i / 2, right = left + i % 2; // 根据i的奇偶性确定回文中心的左右位置
while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
// 如果当前是一个回文子串,则记录数量
ans++;
left--;
right++;
}
}
return ans; // 返回回文子串数量
}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。