微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

1、循环码原理
循环码(cycle code),是一种线性分组码。具有线性码的一般性质外,还具有循环性。
循环性是指任一码组循环一位以后,仍然为该码中的一个码组。
即将最右端的一个码元移至左端,或者将最左端的一个码元移至右端,仍然为该码中的一个码组。
一个循环码的例子
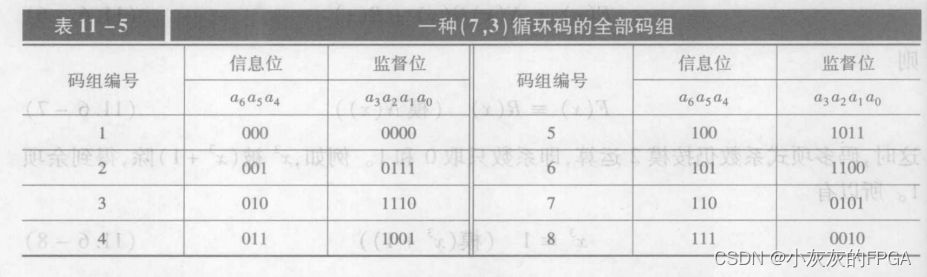
长度n的循环码组的多项式
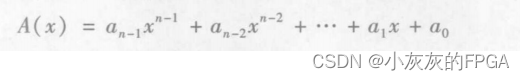
(2)循环码的运算
①码多项式的按模运算
模n(modulo-n)运算
若一个整数(integer)m,满足
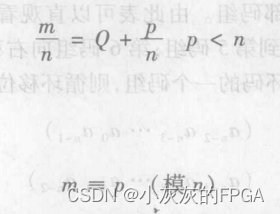
Q为整数
在模n运算下,一个整数m等于它被n除得的余数(remainder)。
码多项式的按模运算,若任一多项式F(x)被一n次多项式N(x)除,得到商式(quotient)Q(x)和一个次数小于n的余式(residue)R(x)
注意:模2运算中,用加法代替了减法

一个重要结论:一个长为n的循环码必定为按模(x^n+1)运算的一个余式
②循环码的生成矩阵G
在循环码中,一个(n,k)码有2^k个不同码组。
g(x)必须是一个常数项不为“0”的(n-k)次多项式,而且这个g(x)还是(n,k)码中次数为(n-k)的唯一一个多项式。
以唯一的(n-k)次多项式g(x)为码生成多项式
可得到循环码的生成矩阵G

③任一(n,k)循环码的生成多项式
任一循环码多项式A(x)都是g(x)的倍式,即A(x)=h(x)×g(x)
生成多项式g(x)是一个(n-k)次多项式
x^k×g(x)是一个n次多项式
进行模(x^n+1)运算可得
(xk×g(x))/(xn+1) = Q(x)+A(x)/(x^n+1)
左端分子和分母都是n次多项式,故Q(x)=1
(xk×g(x))=(xn+1)+h(x)×g(x)
(xn+1)=g(x)×(xk+h(x))
生成多项式g(x)应该是(x^n+1)因子中的一个(n-k)次多项式
④循环码的编码方法
在编码时,根据给定的(n,k)值选定生成多项式g(x),即从(x^n+1)的因子中选一个(n-k)次多项式作为g(x)
具体编码规则:
设m(x)为信息码多项式,其次数小于k
x^(n-k)×m(x)的次数必定小于n,即在信息码后面附加上(n-k)个“0”
余式r(x)=g(x)/(x^(n-k)×m(x)),次数必定小于g(x)的次数(n-k)
余式r(x)与x^(n-k)×m(x)相加,得到码多项式
一个以(7,3)码为例分析:
第一步:
信息码为110,m(x)=x ^ 2+x
n=7,k=3,n-k=4
x ^ (n-k)×m(x)=x ^ 4×(x ^ 2+x)=x ^ 6+x ^ 5,即1100000
第二步:
x ^ n+1=x ^ 7+1=(x+1)×(x ^ 3+x ^ 2+1)×(x ^ 3+x+1)
循环码的生成多项式g(x)有两个:
(x+1)×(x ^ 3+x ^ 2+1)=x ^ 4+x ^ 2+x+1
(x+1)×(x ^ 3+x+1)=x ^ 4+x ^ 3+x ^ 2+1
用g(x)除x^(n-k)×m(x),得到商Q(x)和余式r(x)
(x ^ 6+x ^ 5)/(x ^ 4+x^ 2+x+1)=(x ^ 2+x+1)+(x ^ 2+1)/(x ^ 4+x ^ 2+x+1)
即Q(x)=(x2+x+1);r(x)=(x2+1)
第三步:
编码为:A(x)=x^(n-k)×m(x)+r(x)=1100000+101=1100101
⑤循环码的解码方法
接收端解码有两个要求:检错和纠错
通过余项是否为零来判断接收码组中有无错码
传输过程中为发送错误时,接收码组B(x)与发送码组A(x)相同,即B(x)必定能被g(x)整除;
传输过程中发生错误时,B(x)被g(x)除时,可能存在除不尽而有余项;
B(x)/g(x)=Q(x)+r(x)/g(x)
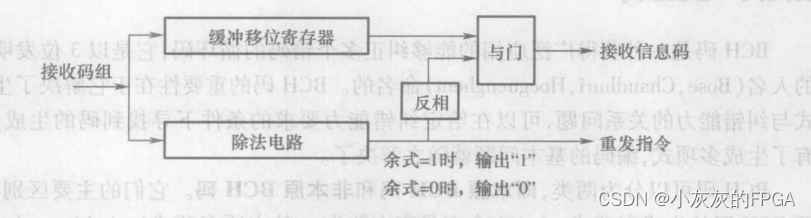
检错解码器的原理,一个除法电路和缓冲移位寄存器
除法电路与发送端编码器的除法电路相同,进行B(x)/g(x)的运算
余项为“0”,将暂存于缓冲器中的接收码组发送到解码器的输出端
余项不为“0”,将缓存器中的接收码组删除,并向发送端发出一个重发指令,要求重发一次该码组
捕错解码法,具体解码规则:
第一步:
用生成多项式g(x)除接收码组B(x),得出余式r(x)
第二步:
按余式r(x),用查表法或其他计算获得错误图样E(x),确定错码的位置
第三步:
从B(x)中减去E(x),得到已经纠正错码的原发送码组A(x)
通信原理板块——线性分组码之循环码
news2026/2/12 20:00:34
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1201575.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
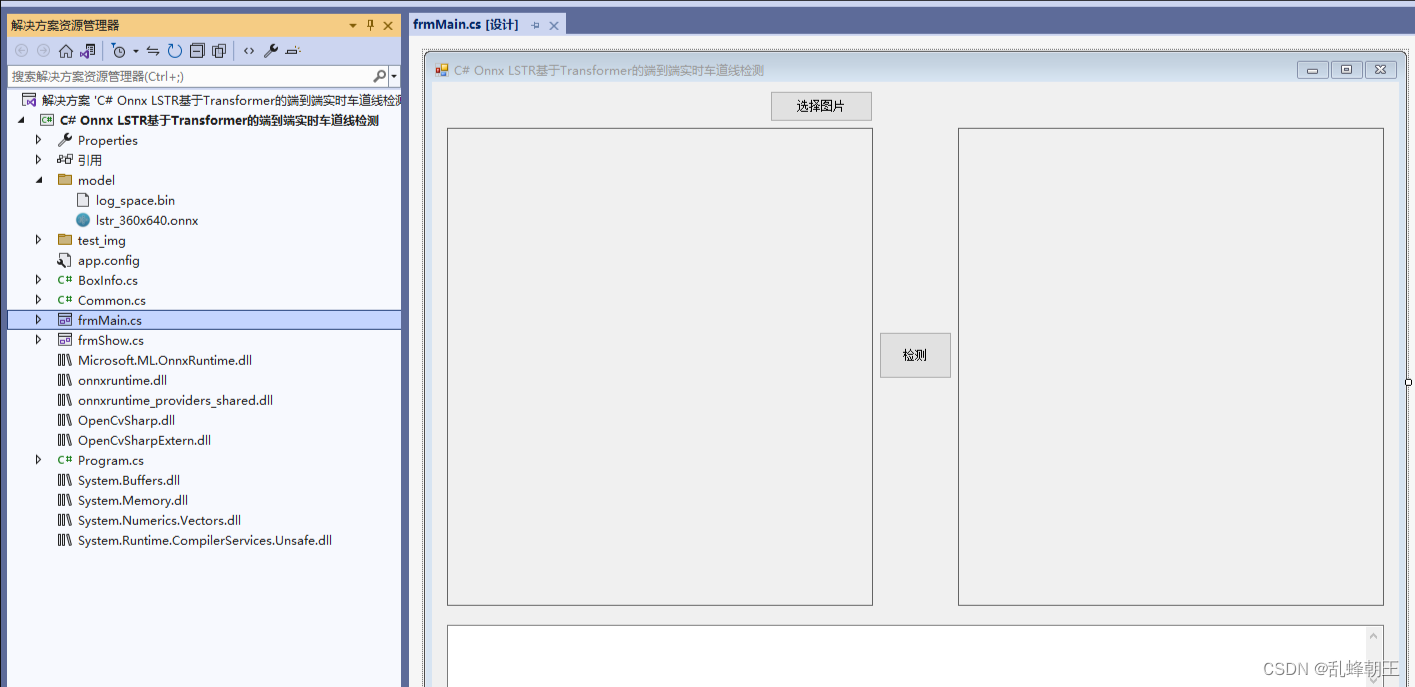
C# Onnx LSTR 基于Transformer的端到端实时车道线检测
目录
效果
模型信息
项目
代码
下载 效果 模型信息
lstr_360x640.onnx
Inputs ------------------------- name:input_rgb tensor:Float[1, 3, 360, 640] name:input_mask tensor:Float[1, 1, 360, 640] -----------------…
罕见!阿里云全系产品崩了。。
作者:苍何,前大厂高级 Java 工程师,阿里云专家博主,CSDN 2023 年 实力新星,土木转码,现任部门技术 leader,专注于互联网技术分享,职场经验分享。 🔥热门文章推荐…
安全认证框架Shrio学习,入门到深度学习,SpringBoot整合Shiro小案例,含代码
权限概述
什么是权限 什么是权限 权限管理,一般指根据系统设置的安全策略或者安全规则,用户可以访问而且只能访问自己被授权的资源,不多不少。权限管理几乎出现在任何系统里面,只要有用户和密码的系统。 权限管理再系统中一般分…
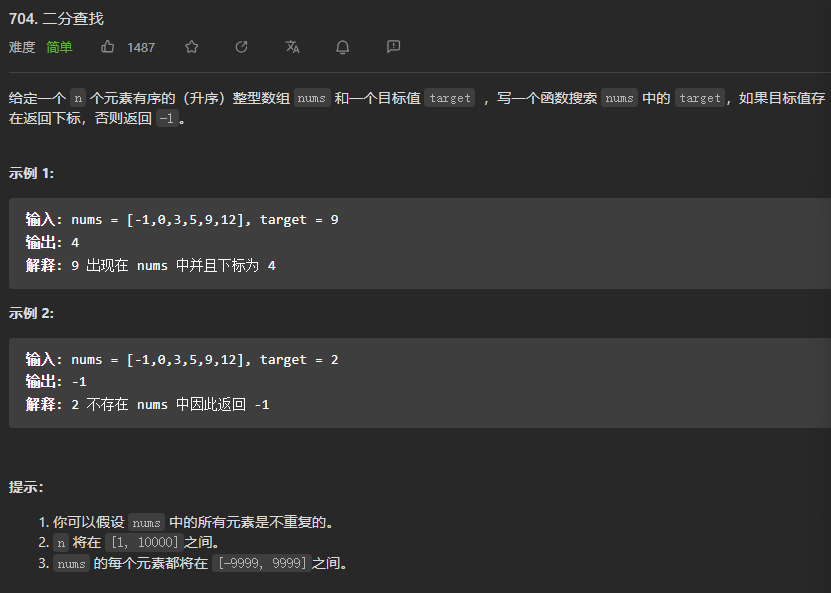
【LeetCode刷题-二分查找】--704.二分查找
704.二分查找 class Solution {public int search(int[] nums, int target) {if(nums.length 0){return -1;}int left 0,right nums.length - 1;while(left < right){int mid (right - left) / 2 left;if(nums[mid] target){return mid;}else if(nums[mid] < targe…
模拟信号数字化--低通抽样与带通抽样
模拟信号数字化 本文主要涉及模拟信号数字化的基本概念,以及对低通抽样与带通抽样以及其公式推导的详细介绍。关于通信原理还有其他文章可参考: 1、信息量、码元、比特、码元速率、信息速率详细解析——实例分析 2、模拟系统的AM信号的调制与频域分析 3、…
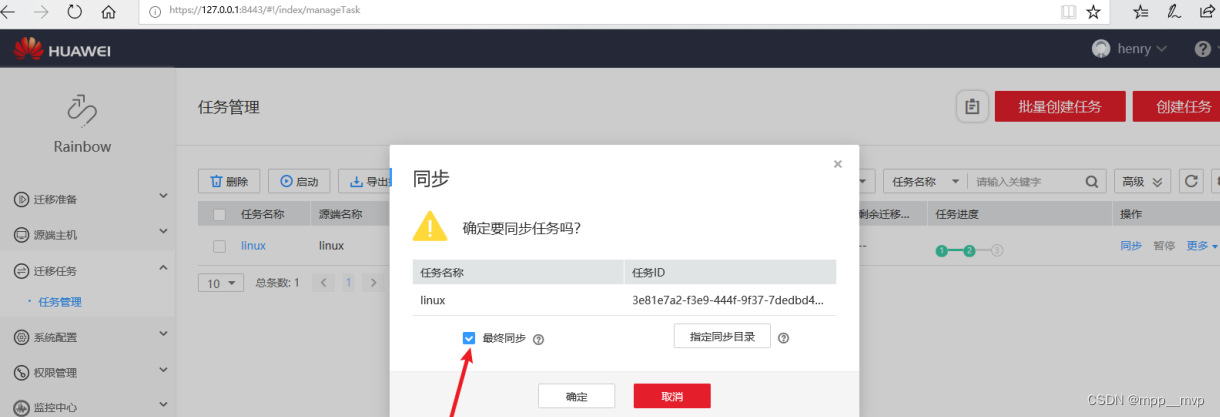
HCIE-Rainbow迁移工具
Rainbow迁移工具
Rainbow迁移工具支持p2v(物理机到虚拟机的迁移) v2v(虚拟机到虚拟机的迁移) Rainbow业务上云迁移: Rainbow迁移到公有云(利用公有云SMS服务,付费) Rainbow迁移到公…
【python】sys-path和模块搜索路径
我们在导入一个模块的时候,比如说:
import math它必然是有搜索路径的,那到底是在哪个目录下面找呢?Python解释器去哪里找这个文件呢?只有找到这个文件才能读取、装载运行该模块文件。
它一般按照如下路径寻找模块文件…
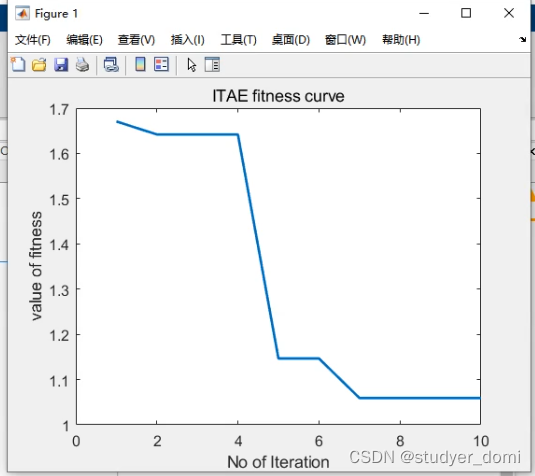
matlab simulink PSO算法优化simulink的PID参数
1、内容简介
略 13-可以交流、咨询、答疑
PSO算法优化simulink的PID参数
2、内容说明
标准的PSO算法优化simulink的PID参数
PSO、粒子群算法、simulink参数优化
3、仿真分析 4、参考论文
略
链接:https://pan.baidu.com/s/1yQ1yDfk-_Qnq7tGpa23L7g 提取码&…
企业知识库建设指南:实用经验分享
企业知识库建设是提升内部协作和客户支持效率的重要举措。一个完善的知识库可以帮助企业集中管理和传播知识,提供便捷的自助服务和丰富的编辑工具,从而提升用户体验和品牌好感度。接下来就分享一些经验,关于该如何构建一个高效的企业知识库。…
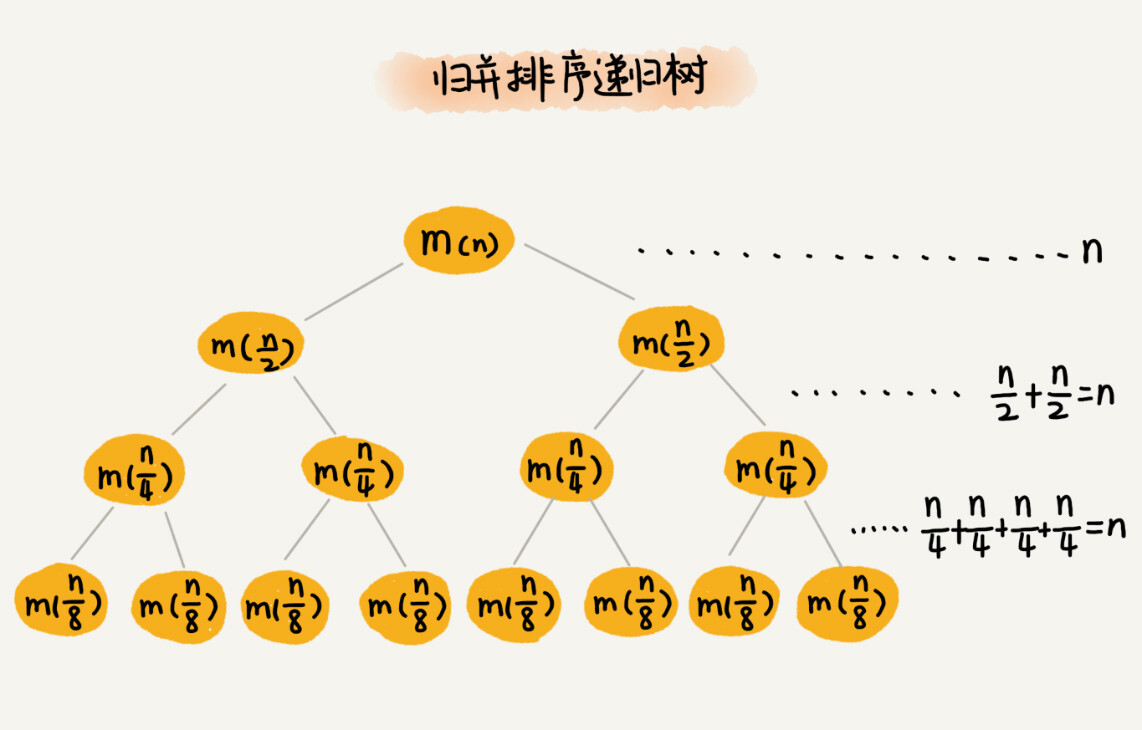
27 _ 递归树:如何借助树来求解递归算法的时间复杂度?
我们都知道,递归代码的时间复杂度分析起来很麻烦。有一个巧妙的方式是借助递归树来分析递归算法的时间复杂度。
递归树与时间复杂度分析
我们前面讲过,递归的思想就是,将大问题分解为小问题来求解,然后再将小问题分解为小小问题。这样一层一层地分解,直到问题的数据规模…
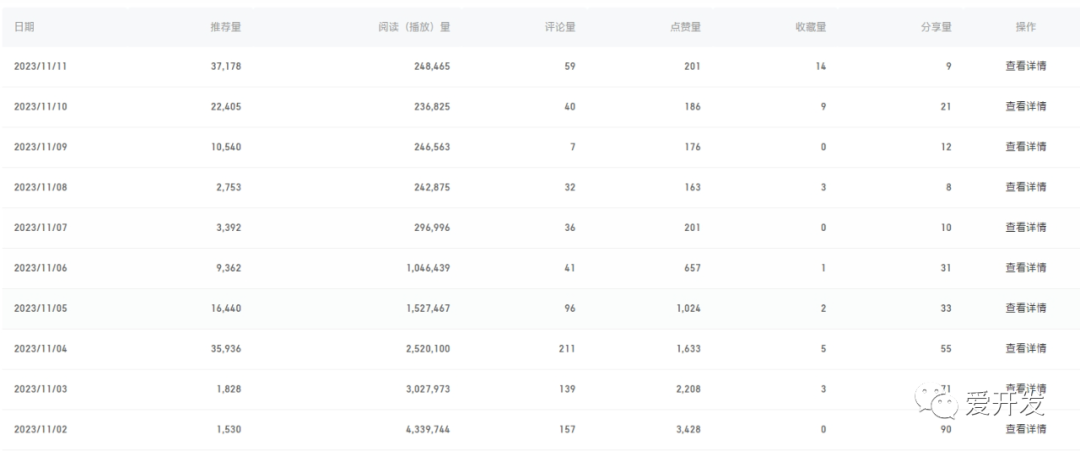
不可思议,才一周,阅读量就突破千万了
这段时间,我发布的文章阅读量看上去还算可以,但我知道,这并不是终点,而是起点。我深知,写作的道路永无止境,只有不断努力,才能在文字的海洋中游得更远。 在这条道路上,我始终坚持用心…
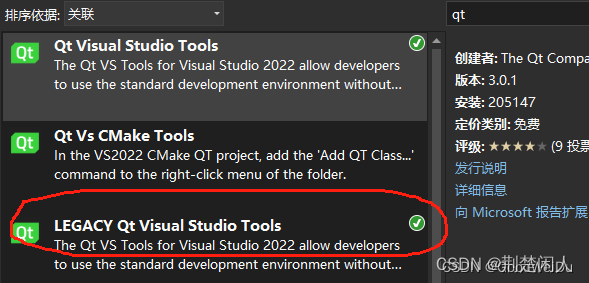
将VS工程转为Qt的pro工程及VS安装Qt插件后没有create basic .pro file菜单问题解决
目录
1. 前言
2. VS工程转为pro工程
3. 没有create basic .pro file菜单 1. 前言 很多小伙伴包括本人,如果是在Windows下开发Qt程序,偏好用Visual Studio外加装个Qt插件进行Qt开发,毕竟Visual Studio确实是功能强大的IDE,但有时…
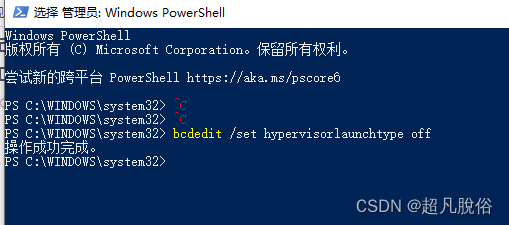
vmware workstation 与 device/credential guard 不兼容
VM虚拟机报错
vmware虚拟机启动时报错:vmware workstation 与 device/credential guard 不兼容: 系统是win10专业版,导致报错原因最终发现是安装了docker,docker自带下载虚拟机Hyper-V,而导致vmware workstation 与 …
基于51单片机篮球控制器12864显示仿真及源程序
一、系统方案 1、本设计采用51单片机作为主控器。 2、比分液晶12864显示。 3、主客队加减分、节数、24秒、复位等功能。 二、硬件设计 原理图如下:
三、单片机软件设计 1、首先是系统初始化 void Timer_0()interrupt 1 { TL0 0x00; TH0 0xDC; Count; if(Coun…
[云原生案例2.3 ] Kubernetes的部署安装 【多master集群架构高可用 ---- (二进制安装部署)】
文章目录 1. Kubernetes多Master集群高可用方案1.1 多节点Master高可用的实现过程1.2 实现高可用方法 2. 新Master节点的部署2.1 前置准备2.2 系统初始化操作2.2.1 关闭防火墙、selinux和swap分区2.2.2 修改主机名,添加域名映射2.2.3 修改内核参数2.2.4 时间同步 2.…
Pinia 状态管理器 菠萝:Option Store风格
Pinia介绍:
Pinia 是 Vue 的专属状态管理库,它允许你跨组件或页面共享状态。
Pinia 大小只有 1kb 左右,超轻量级,你甚至可能忘记它的存在!
相比 Vuex,Pinia 的优点:
更贴合 Vue 3 的 Composition API 风…
从0到0.01入门React | 010.精选 React 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…





![[云原生案例2.3 ] Kubernetes的部署安装 【多master集群架构高可用 ---- (二进制安装部署)】](https://img-blog.csdnimg.cn/b7ca1b55170d4010b9cb31e888d0d5c4.png)