一、蒙特卡洛方法
这里将介绍一个学习方法和发现最优策略的方法,用于估计价值函数。与前文不同,这里我们不假设完全了解环境。蒙特卡罗方法只需要经验——来自实际或模拟与环境的交互的样本序列的状态、动作和奖励。从实际经验中学习是引人注目的,因为它不需要任何关于环境动态的先验知识,但仍然可以实现最优行为。从模拟经验中学习也很强大。尽管需要一个模型,但该模型只需要生成样本转换,而不是动态规划所需的完整概率分布的所有可能转换。令人惊讶的是,在很多情况下,根据所需概率分布生成经验样本很容易,但获得分布的显式形式是不可行的。
蒙特卡罗方法是解决强化学习问题的方法,它基于平均样本回报。为了确保可定义回报可用,在这里我们将蒙特卡罗方法仅定义为针对离散任务的方法。即我们假设经验分为回合,并且所有回合最终都会终止,无论选择什么动作。只有在完成回合后才会更改价值估计和策略。因此,蒙特卡罗方法可以是逐回合的增量,但不能是逐步(在线)的增量。术语“蒙特卡罗”通常更广泛地用于任何涉及大量随机组件的估计方法。在这里,我们将其专门用于基于平均完整回报(而不是从部分回报中学习的方法)的方法。
蒙特卡罗方法对每个状态-动作对进行采样和平均回报,就像我们在前文对每个动作进行采样和平均奖励一样。主要的区别在于,现在有多个状态,每个状态都像不同的问题(如联想搜索或上下文)一样,而且这些不同的问题是相互关联的。也就是说,在一个状态下采取一个行动后的回报取决于在同一回合中后来采取的行动。因为所有的行动选择都在进行学习,所以从更早的状态来看,这个问题就变成了非平稳的。
为了处理非平稳性,我们采用了通用策略迭代(GPI)的想法。在那里,我们从MDP的知识中计算值函数,在这里,我们从样本回报中学习值函数与相应的策略仍然以相同的方式相互作用以获得最优性(GPI)。与DP一样,我们首先考虑预测问题(计算固定任意策略π的vπ和qπ),然后进行政策改进,最后是控制问题以及通过GPI解决。这些来自DP的想法都被扩展到了只有样本经验可用的蒙特卡罗情况下。
二、蒙特卡洛预测
我们首先考虑使用蒙特卡罗方法学习给定策略的状态值函数。注意,一个状态的值是期望的回报,也就是从该状态开始的期望累积未来折扣奖励。那么,从经验中估计它的一个明显方法就是简单地将该状态后观察到的回报进行平均。随着更多的回报被观察到,平均值应该收敛到期望值。这个想法是所有蒙特卡罗方法的基础。
特别是,假设我们希望估计π策略下状态s的值vπ(s),给定一组遵循π并通过s获得的状态转移序列。在每个回合中,状态s的每次出现称为对s的一次。当然,在同一个回合中,s可能被多次;让我们称在回合中对s的第一次为s的第一次。第一次蒙特卡罗方法估计vπ(s)为在第一次s后的回报的平均值,而每次蒙特卡罗方法则将所有s后的回报进行平均。这两种蒙特卡罗方法非常相似,但具有稍微不同的理论性质。蒙特卡罗方法是研究很广泛,以程序形式显示在图1中。

图1
图1中我们使用大写字母V表示近似值函数,因为在初始化之后,它很快就会变成一个随机变量。
对于首次使用蒙特卡罗方法和每次使用蒙特卡罗方法,当次数(或首次次数)趋于无穷时,它们都会收敛到vπ(s)。对于首次蒙特卡罗方法的情况,这一点很容易理解。在这种情况下,每次返回都是vπ(s)的独立、相同分布的估计,具有有限方差。根据大数定律,这些估计的平均值序列收敛到它们的期望值。每个平均值本身都是一个无偏估计,其误差的标准偏差为1/√n,其中n是平均值的数量。每次蒙特卡罗方法不太直观,但其估计也渐近收敛到vπ(s)(Singh和Sutton,1996)。蒙特卡罗方法的使用最好通过一个例子来说明。
三、典型例子
21点,又称黑杰克,是一种广受欢迎的赌场牌戏。游戏的目标是在不超出21点的情况下,尽可能获得高数值的牌。所有花牌都算作10点,而一张A可以算作1点或11点。我们考虑的是每个玩家独立与庄家对抗的版本。游戏开始时,庄家和玩家都会得到两张牌。庄家的一张牌是明牌,另一张是暗牌。如果玩家立即得到21点(一张A和一张10),那么就称为“自然”,除非庄家也有自然,否则玩家获胜。如果玩家没有自然,那么他可以要求额外的牌,一张一张地要(继续要牌),直到他停止(停牌)或超过21点(爆牌)。如果他爆牌,他就输了;如果他停牌,那么就轮到庄家。庄家根据固定的策略决定是否要牌或停牌,没有选择:他在任何总和为17点或更高的情况下停牌,否则就继续要牌。如果庄家爆牌,那么玩家就赢了;否则,结果(赢、输或平局)由谁的最终总和最接近21点决定。
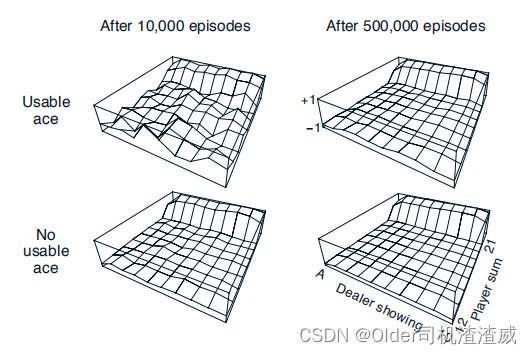
图2
图2中黑杰克策略的近似状态值函数,只在20或21点停牌,通过蒙特卡洛策略评估计算。玩二十一点被自然地制定为一段有限的MDP。 每一局二十一点是一个情节。 对于赢、输和平局,分别给予+1、-1和0的奖励。 在一局比赛中所有的奖励都是零,我们不进行贴现(γ = 1);因此这些末端奖励也是回报。 玩家的行动是击打或停牌。 状态依赖于玩家的牌和庄家的明牌。 我们假设卡片是从一个无限的套牌(即替换)中发出的,因此没有必要追踪已经发出的卡片。 如果玩家持有一张可以计为11的A牌而不会爆牌,那么这张A牌被称为可用。 在这种情况下,它总是被计为11,因为把它计为1会使总和小于或等于11,在这种情况下,没有做出决定,因为显然玩家应该一直击打。 因此,玩家根据三个变量做出决定:他当前的总和(12-21),庄家的一个明牌(A-10),以及他是否持有一张可用的A牌。 这总共有200个状态。
考虑如果在玩家总和为20或21时停牌,否则就击打的策略。 通过蒙特卡罗方法找到此策略的状态值函数,模拟许多二十一点游戏并平均每个状态后的回报。 请注意,在此任务中,相同的状态在同一情节中永远不会重复发生,因此没有首次访问和每次访问的MC方法之间的区别。 通过这种方式,我们获得了图2中所示的状态值函数的估计值。具有可用A牌的状态的估计值不太确定也不太规律,因为这些状态不太常见。 无论如何,经过50万场比赛后,价值函数被很好地逼近。

![web:[网鼎杯 2018]Fakebook](https://img-blog.csdnimg.cn/e4705e1ba61f4319a4206c954fb7a006.png)






![[N-133]基于springboot,vue小说网站](https://img-blog.csdnimg.cn/3741f74602be40e9aededfda04e88ff4.png)