箱线图 boxplot
- 简述
- 原理
- 绘制方法
- python - matplotlib
- 加载功能模块
- 加载数据
- 绘制boxplot
- python - seaborn
- 加载功能模块
- 加载数据
- 绘制boxplot
- R - ggplot
- 加载功能模块
- 加载数据
- 绘制boxplot
简述
因图形形状如箱子而得名。箱线图常用于展示一组连续型数据的分散情况。学术界普遍认为,箱线图由美国数学家M.E.斯皮尔于1960年提出,由美国统计学家J.W.图基于1977年完善并正式发表。在后续的发展中,箱线图的绘制过程经历了一些重要调整。主要调整包括箱子的宽度,上下边缘的确定标准,异常值的标识方法等。
原理
箱线图利用一组数据的分位数信息进行数据展示。箱形图分为中心、延伸以及分布状态的全部范围。将一组数据从大到小排列,分别计算出这组数据的上边缘,四分之一分位数( Q 1 Q_1 Q1)、中位数( Q 2 Q_2 Q2)、四分之三分位数( Q 3 Q_3 Q3)、下边缘,有时还包括一个异常值。四分位距(interquantile range; IQR)是四分之三分位与四分之一分位数的差值, I Q R = Q 3 − Q 1 IQR=Q_3-Q_1 IQR=Q3−Q1,主要反映连续型数据的离散程度。
绘制方法
在不同软件中,箱线图的绘制方法有微小差异,这里仅说明常见的箱线图的绘制方法。
- 先根据三个分位数 Q 1 Q_1 Q1、 Q 2 Q_2 Q2、 Q 3 Q_3 Q3画出中间的盒子。
- 由 Q 3 Q_3 Q3至 Q 1 − 1.5 × I Q R Q_1-1.5\times IQR Q1−1.5×IQR区间内的最大值向盒子的顶端连线,由 Q 1 Q_1 Q1至 Q 1 − 1.5 × I Q R Q_1-1.5\times IQR Q1−1.5×IQR区间内的最小值向盒子的底部连线。
- 处于 Q 1 − 1.5 × I Q R Q_1-1.5\times IQR Q1−1.5×IQR至 Q 1 − 3 × I Q R Q_1-3\times IQR Q1−3×IQR或者 Q 3 + 1.5 × I Q R Q_3+1.5\times IQR Q3+1.5×IQR至 Q 3 + 3 × I Q R Q_3+3\times IQR Q3+3×IQR范围内的数据用圆点标出,称为离群值(outliers)。
- 大于 Q 3 + 3 × I Q R Q_3+3\times IQR Q3+3×IQR或者小于 Q 1 − 3 × I Q R Q_1-3\times IQR Q1−3×IQR的用星号标出,称为异常值(extremes)。
python - matplotlib
加载功能模块
import matplotlib.pyplot as plt
import pandas as pd
加载数据
# 加载数据集
from sklearn.datasets import load_iris
# 把数据集转换为一个DataFrame
data = load_iris()
df = pd.DataFrame(data=data.data,columns=data.feature_names)
df['target'] = data.target
df['target'] = df['target'].replace([0,1,2],['setosa', 'versicolor', 'virginica'])
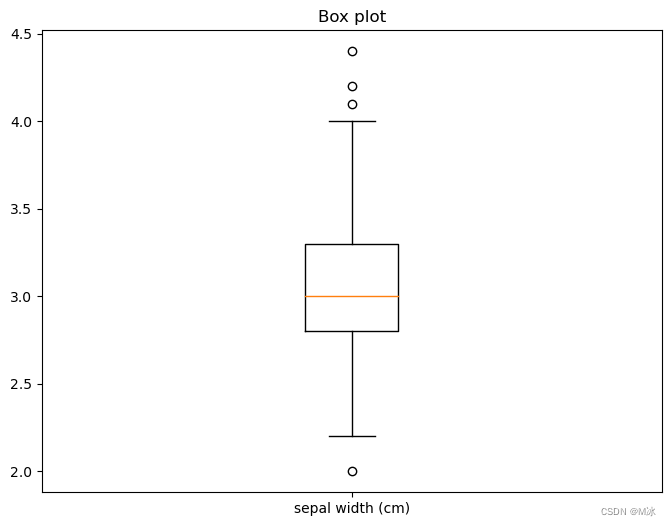
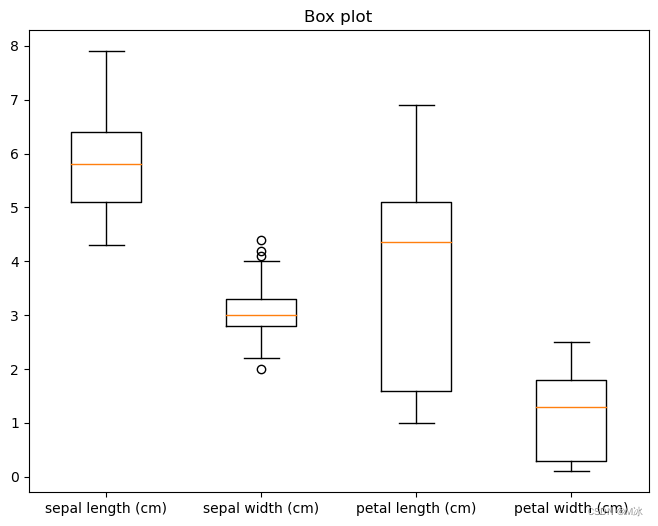
绘制boxplot
# 设置画布大小
plt.figure(figsize=(8,6))
# 设置绘制的数据
plt.boxplot(df[df.columns[0:-1]])
# 设置图的标题
plt.title('Box plot')
# 设置X轴(横坐标轴)的显示内容
plt.xticks([1, 2, 3, 4],df.columns[0:-1] )
plt.show()
python - seaborn
加载功能模块
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
加载数据
# 加载数据集
from sklearn.datasets import load_iris
# 把数据集转换为一个DataFrame
data = load_iris()
df = pd.DataFrame(data=data.data,columns=data.feature_names)
df['target'] = data.target
df['target'] = df['target'].replace([0,1,2],['setosa', 'versicolor', 'virginica'])
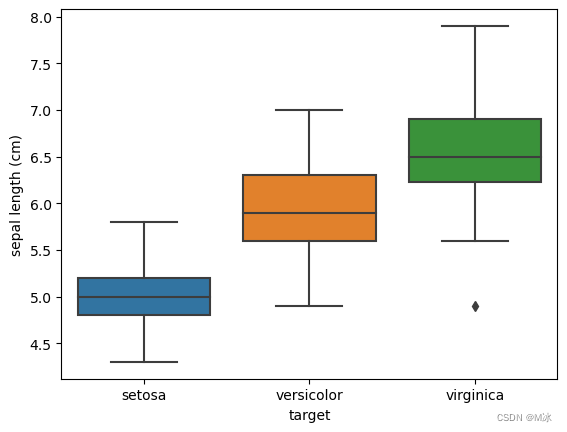
绘制boxplot
# 设置绘制的数据
sns.boxplot(x='target', y = 'sepal length (cm)',data= df )
plt.show()
R - ggplot
加载功能模块
# 绘图包
library(ggplot2)
# 数据处理包
library(tidyverse)
加载数据
# 加载自带数据集
library(mpg)
# 删除数据中的空值
df <- mpg
df <- drop_na(df)
绘制boxplot
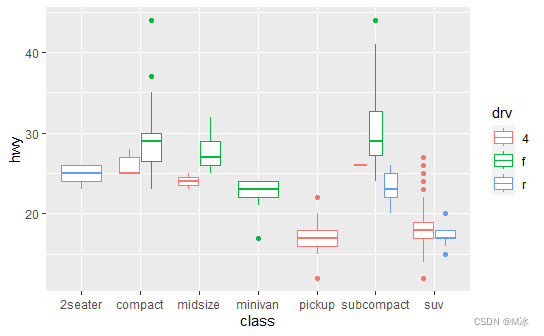
# 绘制箱线图
ggplot(mpg,aes(x=class,y=hwy,color=drv)) +
geom_boxplot()