文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
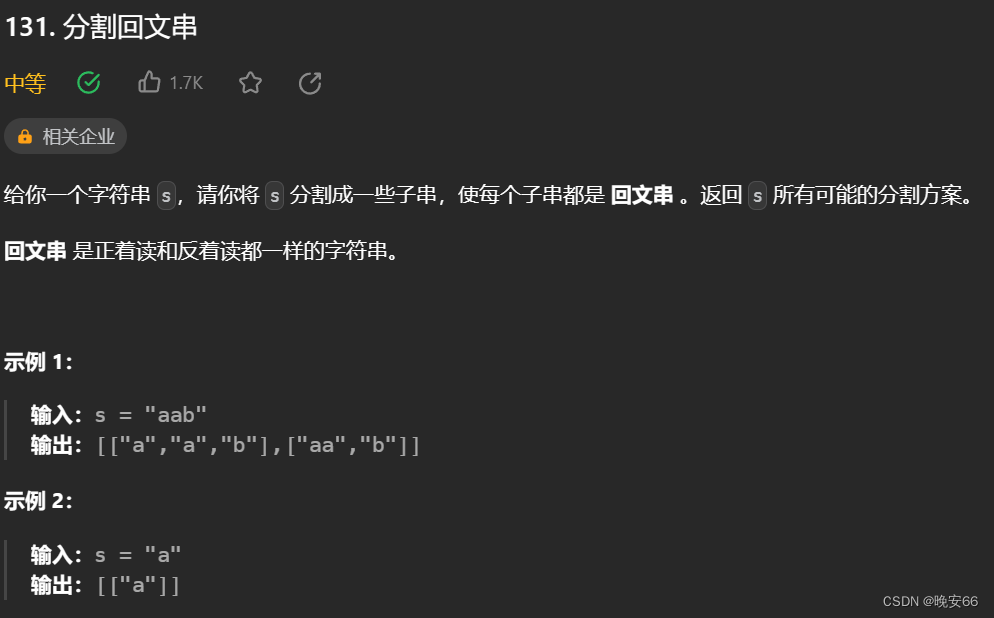
二、解法
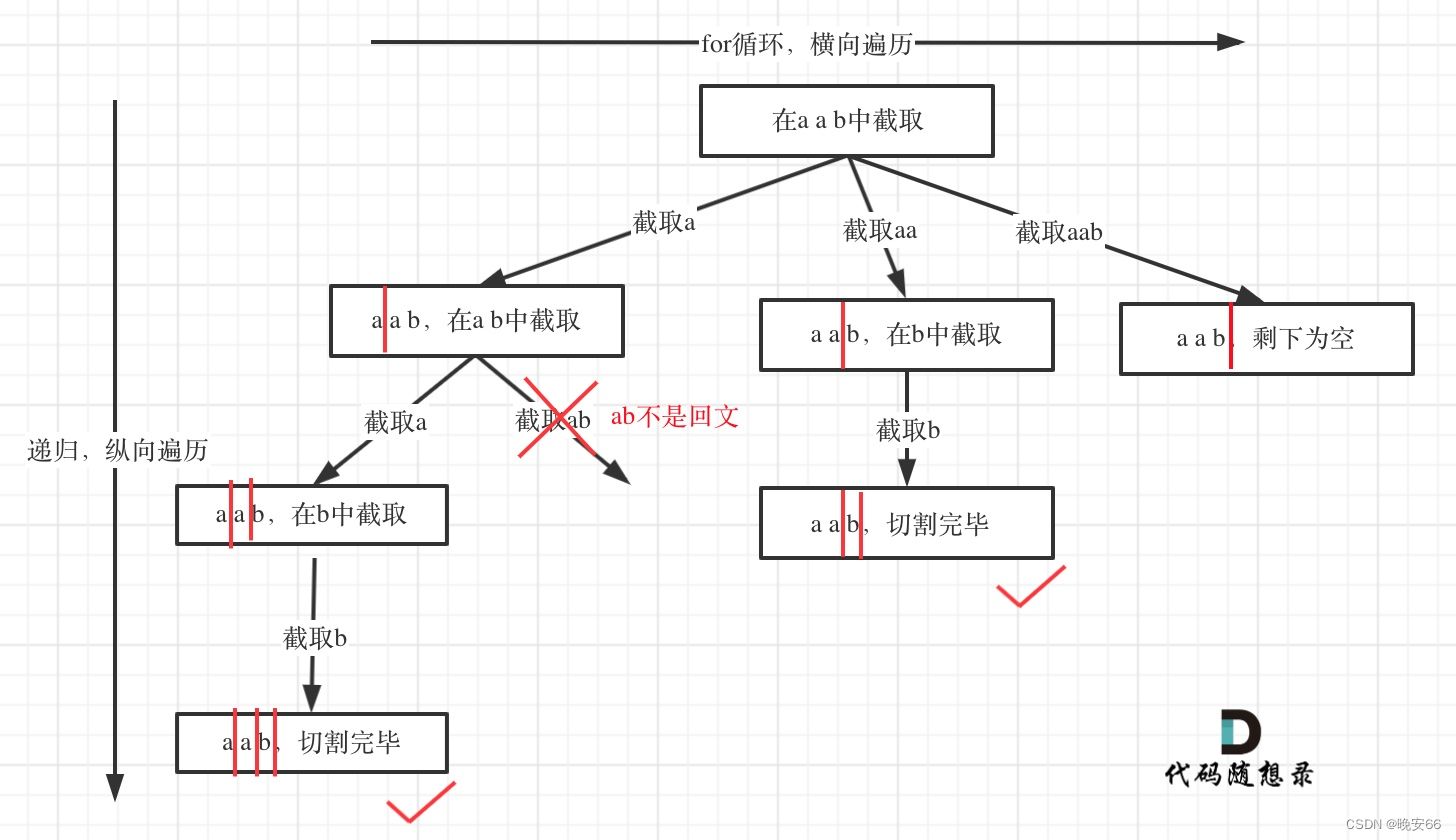
思路分析:本题仍然使用回溯算法的一般结构。加入了一个判断是否是回文串的函数,利用起始和终止索引进行判断,字符串使用引用输入, 减少传参的时间开销。将开始索引大于等于字符串长度作为终止条件,表示已经找到一个回文串的组合。此外,进一步改进算法的性能,可以建立一个查找数组,提前算出分割的子串是否为回文串,使用时直接判断即可。
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
程序如下:
class Solution {
private:
vector<vector<string>> result;
vector<string> path;
bool isSymmetry(const string& s, const int start, const int end) {
bool flag = true;
for (int i = start, j = end; i <= j; i++, j--) {
if (s[i] != s[j]) {
flag = false;
break;
}
}
return flag;
}
void backtracking(const string& s, int startIndex) {
if (startIndex >= s.size()) {
result.push_back(path);
return;
}
for (int i = startIndex; i < s.size(); i++) {
if (isSymmetry(s, startIndex, i)) { // 是回文串才加入结果数组
string str = s.substr(startIndex, i - startIndex + 1);
path.push_back(str);
}
else { // 不是回文串跳过
continue;
}
backtracking(s, i + 1);
path.pop_back();
}
}
public:
vector<vector<string>> partition(string s) {
backtracking(s, 0);
return result;
}
};
复杂度分析:
- 时间复杂度: O ( n ∗ 2 n ) O(n*2^n) O(n∗2n), n代表字符串长度。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2)。
三、完整代码
# include <iostream>
# include <string>
# include <vector>
using namespace std;
class Solution {
private:
vector<vector<string>> result;
vector<string> path;
bool isSymmetry(const string& s, const int start, const int end) {
bool flag = true;
for (int i = start, j = end; i <= j; i++, j--) {
if (s[i] != s[j]) {
flag = false;
break;
}
}
return flag;
}
void backtracking(const string& s, int startIndex) {
if (startIndex >= s.size()) {
result.push_back(path);
return;
}
for (int i = startIndex; i < s.size(); i++) { // 剪枝优化
if (isSymmetry(s, startIndex, i)) { // 是回文串才加入结果数组
string str = s.substr(startIndex, i - startIndex + 1);
path.push_back(str);
}
else { // 不是回文串跳过
continue;
}
backtracking(s, i + 1);
path.pop_back();
}
}
public:
vector<vector<string>> partition(string s) {
backtracking(s, 0);
return result;
}
};
int main() {
string s = "aab";
Solution s1;
vector<vector<string>> result = s1.partition(s);
for (vector<vector<string>>::iterator it = result.begin(); it != result.end(); it++) {
for (vector<string>::iterator jt = (*it).begin(); jt != (*it).end(); jt++) {
cout << *jt << " ";
}
cout << endl;
}
system("pause");
return 0;
}
end