机器人臂是自动化领域中常见的机器人形式,其精确控制对于实现复杂任务具有重要意义。在机器人臂的控制中,PID控制和神经网络控制是两种常用的控制方法。本文将比较PID控制和神经网络控制在机器人臂控制方面的应用,包括控制原理、优缺点以及在不同场景下的适用性。
机器人臂的控制一直是自动化领域中研究的热点之一。PID控制作为一种经典的控制方法,在许多机器人系统中被广泛应用。然而,随着人工智能领域的发展,神经网络控制在机器人臂控制中也逐渐得到应用。本文将比较PID控制和神经网络控制在机器人臂控制方面的应用,为研究和应用者提供参考。
PID控制和神经网络控制的基本原理:
1. PID控制:
PID控制是一种经典的反馈控制方法,通过不断调节比例、积分和微分部分来实现对系统的控制。PID控制器根据误差信号来产生控制输出,并根据系统的反馈信号进行调整,以实现期望的控制效果。
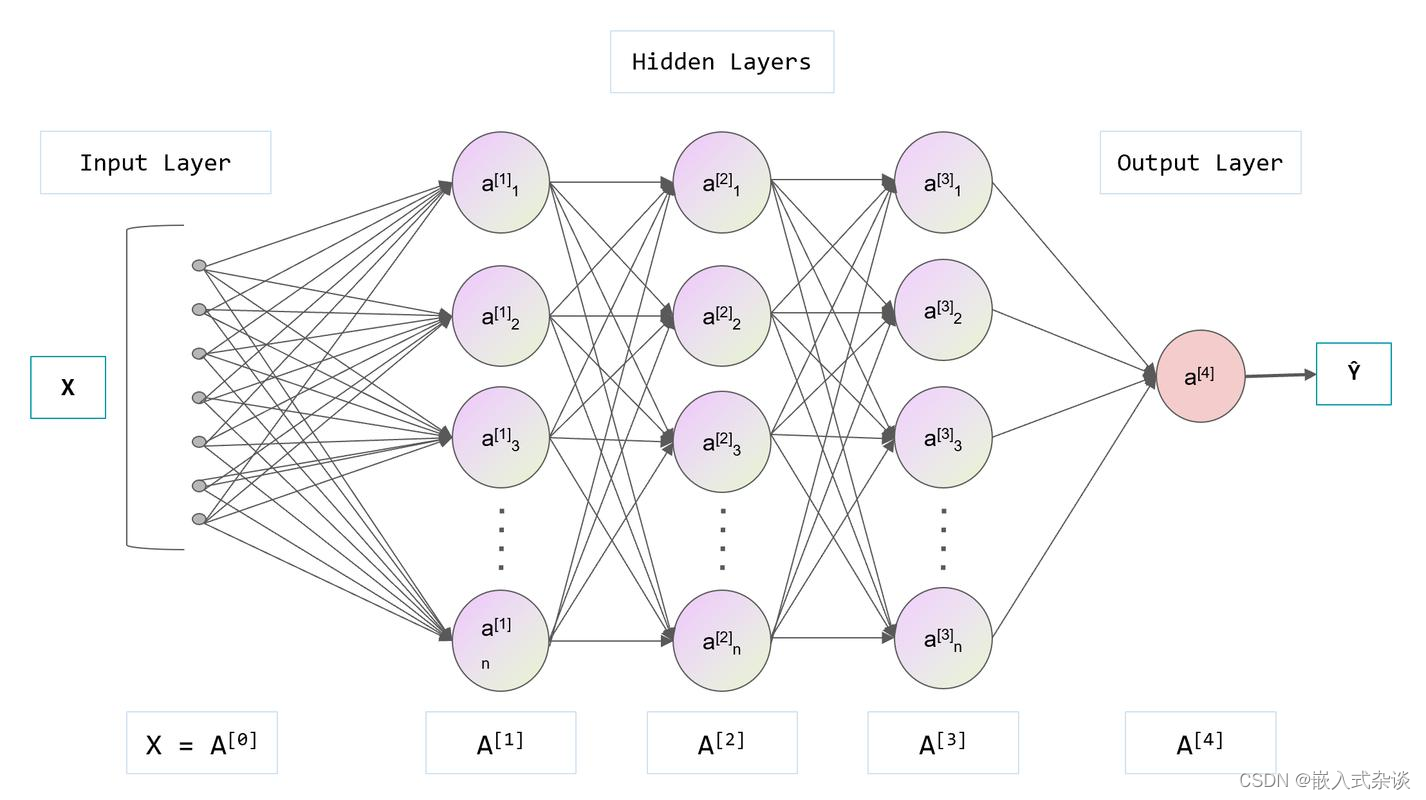
2. 神经网络控制:
神经网络控制是一种基于人工神经网络的控制方法,通过输入-处理-输出的方式建立神经网络模型。神经网络通过学习训练数据来优化网络参数,并根据输入信号产生相应的输出控制信号,实现控制目标。
PID控制和神经网络控制的比较:
1. 控制性能:
PID控制通过调节控制参数来实现对机器人臂的精确控制,具有较高的控制性能,尤其在简单线性系统中效果显著。神经网络控制因其具备非线性建模能力,能够适用于复杂系统的控制,能够应对更多的非线性、时变和不确定性问题。
2. 参数调整和稳定性:
PID控制需要通过手工调整参数来适应不同的系统和任务,对参数调节的要求较高,且对系统的稳定性要求严格。神经网络控制通过学习训练数据自适应地调整网络参数,能够自动拟合复杂系统的模型,并具备一定的鲁棒性和自适应性。
3. 鲁棒性和适应性:
PID控制在面对噪声、干扰和参数变化时可能会出现较差的鲁棒性和适应性。神经网络控制通过学习数据集的特征,具有较强的鲁棒性和适应能力,能够在一定程度上应对系统的变化和不确定性。
4. 计算复杂度和实时性:
PID控制是一种简单的控制算法,计算复杂度低,适用于实时控制要求较高的场景。神经网络控制由于需要进行反向传播训练,计算复杂度较高,对计算资源和实时性要求较高。
适用性和应用场景比较:
1. PID控制适用于简单的线性系统,例如传送带上的物品定位、工业生产线上的装配等场景。
2. 神经网络控制适用于非线性、复杂系统的控制,例如机器人臂在复杂环境中的路径规划、物体识别和抓取等场景。
结论:
本文对PID控制和神经网络控制在机器人臂控制方面的应用进行了比较。PID控制具有较高的精确性和控制性能,适用于简单线性系统控制;神经网络控制具有较强的非线性建模能力和适应性,适用于复杂系统的控制。选择合适的控制方法应根据系统的特性和任务需求进行综合考虑。
嵌入式物联网的学习之路非常漫长,不少人因为学习路线不对或者学习内容不够专业而错失高薪offer。不过别担心,我为大家整理了一份150多G的学习资源,基本上涵盖了嵌入式物联网学习的所有内容。点击这里,0元领取学习资源,让你的学习之路更加顺畅!记得点赞、关注、收藏、转发哦。
点击链接扫码进入嵌入式交流群