数字滤波器分析---频率响应

幅值、相位、冲激和阶跃响应、相位和群延迟、零极点分析。

分析滤波器的频域和时域响应。可视化复平面中的滤波器极点和零点。

频率响应

数字域

freqz 使用基于 FFT 的算法来计算数字滤波器的 Z 变换频率响应。具体来说，语句

[h,w] = freqz(b,a,p)

返回数字滤波器的包含 p 个点的复频率响应 H(ejω)。

在其最简单的形式中，freqz 接受滤波器系数向量 b 和 a 以及整数 p（该整数指定计算频率响应所用的点的数量）。freqz 以弧度/秒为单位返回向量 h 中的复频率响应，以及向量 w 中的实际频率点。

freqz 可以接受其他参数，例如采样频率或由任意数量的频率点构成的向量。以下示例求 12 阶切比雪夫 I 型滤波器的 256 点频率响应。调用 freqz 将采样频率 fs 指定为 1000 Hz：

[b,a] = cheby1(12,0.5,200/500);
[h,f] = freqz(b,a,256,1000);

由于参数列表包含采样频率，因此 freqz 返回向量 f，其中包含在频率响应计算中使用的 0 到 fs/2 之间的 256 个频率点。

注意

此工具箱使用单位频率是奈奎斯特频率的约定，定义为采样频率的一半。所有基本滤波器设计函数的截止频率参数均用奈奎斯特频率进行归一化处理。例如，对于采样频率为 1000 Hz 的系统，300 Hz 等于 300/500 = 0.6。要将归一化频率转换为围绕单位圆的角频率，请乘以 π。要将归一化频转换回赫兹，请乘以采样频率的一半。

如果您在不带输出参数的情况下调用 freqz，它会同时绘制幅值对频率的图和相位对频率的图。例如，截止频率为 400 Hz、基于 2000 Hz 的采样频率的九阶巴特沃斯低通滤波器是：

[b,a] = butter(9,400/1000);

要计算此滤波器的 256 点复频率响应，并使用 freqz 绘制幅值和相位，请使用

freqz(b,a,256,2000)

freqz 也可以接受由任意数量的频率点构成的向量，以用于频率响应计算。例如，

w = linspace(0,pi);
h = freqz(b,a,w);

计算由向量 b 和 a 定义的滤波器在 w 的频率点处的复频率响应。频率点可以是 0 到 2π 范围内的值。要指定从零到采样频率的频率向量，请在参数列表中同时包括频率向量和采样频率值。

下列示例说明如何计算和显示数字频率响应。

传递函数的频率响应

计算并显示由以下传递函数描述的三阶 IIR 低通滤波器的幅值响应：

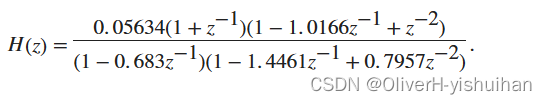
将分子和分母表示为多项式卷积。求分布在整个单位圆上的 2001 个点上的频率响应。

b0 = 0.05634;
b1 = [1  1];
b2 = [1 -1.0166 1];
a1 = [1 -0.683];
a2 = [1 -1.4461 0.7957];

b = b0*conv(b1,b2);
a = conv(a1,a2);

[h,w] = freqz(b,a,'whole',2001);

绘制以分贝表示的幅值响应。

plot(w/pi,20*log10(abs(h)))
ax = gca;
ax.YLim = [-100 20];
ax.XTick = 0:.5:2;
xlabel('Normalized Frequency (\times\pi rad/sample)')
ylabel('Magnitude (dB)')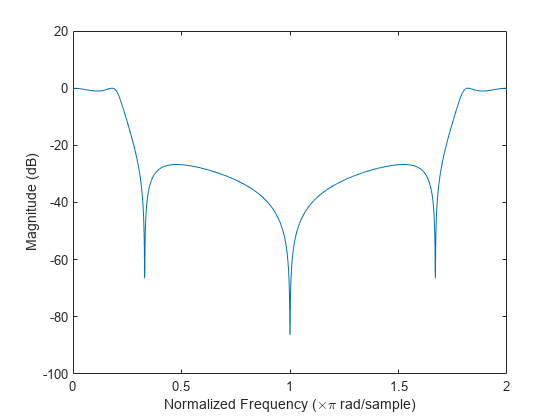

FIR 带通滤波器的频率响应

设计一个 FIR 带通滤波器，通带在 0.35π 和 0.8π 弧度/采样点之间，波纹为 3 dB。第一个阻带是从 0 到 0.1π 弧度/采样点，衰减为 40 dB。第二个阻带是从 0.9π 弧度/采样点到奈奎斯特频率，衰减为 30 dB。计算频率响应。同时以线性单位和分贝绘制其幅值。突出显示通带。

sf1 = 0.1;
pf1 = 0.35;
pf2 = 0.8;
sf2 = 0.9;
pb = linspace(pf1,pf2,1e3)*pi;

bp = designfilt('bandpassfir', ...
    'StopbandAttenuation1',40, 'StopbandFrequency1',sf1,...
    'PassbandFrequency1',pf1,'PassbandRipple',3,'PassbandFrequency2',pf2, ...
    'StopbandFrequency2',sf2,'StopbandAttenuation2',30);

[h,w] = freqz(bp,1024);
hpb = freqz(bp,pb);

subplot(2,1,1)
plot(w/pi,abs(h),pb/pi,abs(hpb),'.-')
axis([0 1 -1 2])
legend('Response','Passband','Location','South')
ylabel('Magnitude')

subplot(2,1,2)
plot(w/pi,db(h),pb/pi,db(hpb),'.-')
axis([0 1 -60 10])
xlabel('Normalized Frequency (\times\pi rad/sample)')
ylabel('Magnitude (dB)')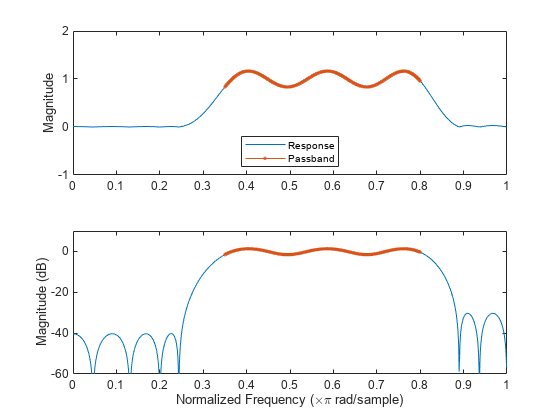

高通滤波器的幅值响应

设计一个三阶高通巴特沃斯滤波器，它具有 0.5π 弧度/采样点的归一化 3-dB 频率。计算它的频率响应。用分贝表示幅值响应，并对其绘图。

[b,a] = butter(3,0.5,'high');
[h,w] = freqz(b,a);

dB = mag2db(abs(h));

plot(w/pi,dB)
xlabel('\omega / \pi')
ylabel('Magnitude (dB)')
ylim([-82 5])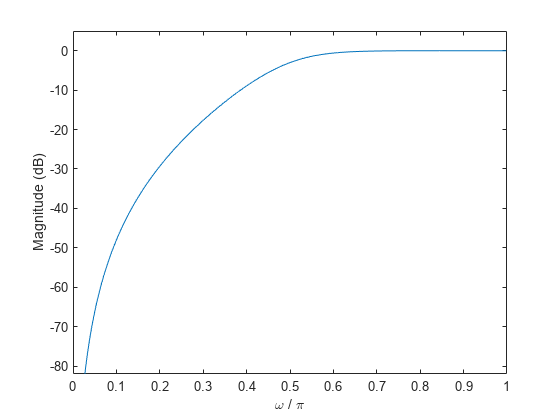

使用 fvtool 重复计算。

fvtool(b,a)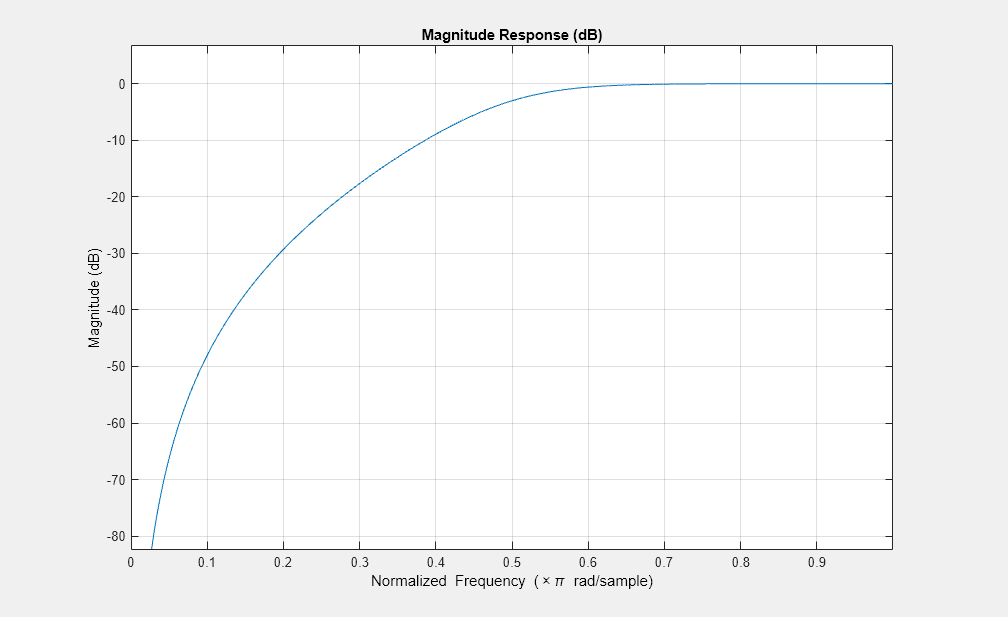

模拟域

freqs 计算由两个输入系数向量 b 和 a 定义的模拟滤波器的频率响应。其运算类似于 freqz 的运算；您可以指定要使用的频率点数量，提供由任意数量的频率点构成的向量，并绘制滤波器的幅值和相位响应。此示例说明如何计算和显示模拟频率响应。

模拟 IIR 低通滤波器的比较

尝试此示例Copy Code  Copy Command

设计截止频率为 2 GHz 的五阶模拟巴特沃斯低通滤波器。乘以 2π 以将频率转换为弧度/秒。计算滤波器在 4096 个点上的频率响应。

n = 5;
fc = 2e9;

[zb,pb,kb] = butter(n,2*pi*fc,"s");
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,4096);

设计一个具有相同边缘频率和 3 dB 通带波纹的五阶切比雪夫 I 型滤波器。计算它的频率响应。

[z1,p1,k1] = cheby1(n,3,2*pi*fc,"s");
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,4096);

设计一个具有相同边缘频率和 30 dB 阻带衰减的 5 阶切比雪夫 II 型滤波器。计算它的频率响应。

[z2,p2,k2] = cheby2(n,30,2*pi*fc,"s");
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,4096);

设计一个具有相同边缘频率和 3 dB 通带波纹、30 dB 阻带衰减的五阶椭圆滤波器。计算它的频率响应。

[ze,pe,ke] = ellip(n,3,30,2*pi*fc,"s");
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,4096);

设计一个具有相同边缘频率的 5 阶贝塞尔滤波器。计算它的频率响应。

[zf,pf,kf] = besself(n,2*pi*fc);
[bf,af] = zp2tf(zf,pf,kf);
[hf,wf] = freqs(bf,af,4096);

对衰减绘图，以分贝为单位。以千兆赫为单位表示频率。比较滤波器。

plot([wb w1 w2 we wf]/(2e9*pi), ...
    mag2db(abs([hb h1 h2 he hf])))
axis([0 5 -45 5])
grid
xlabel("Frequency (GHz)")
ylabel("Attenuation (dB)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

       巴特沃斯和切比雪夫 II 型滤波器具有平坦的通带和宽过渡带。切比雪夫 I 型和椭圆滤波器转降更快，但有通带波纹。切比雪夫 II 型设计函数的频率输入设置阻带的起点，而不是通带的终点。贝塞尔滤波器沿通带具有大致恒定的群延迟。