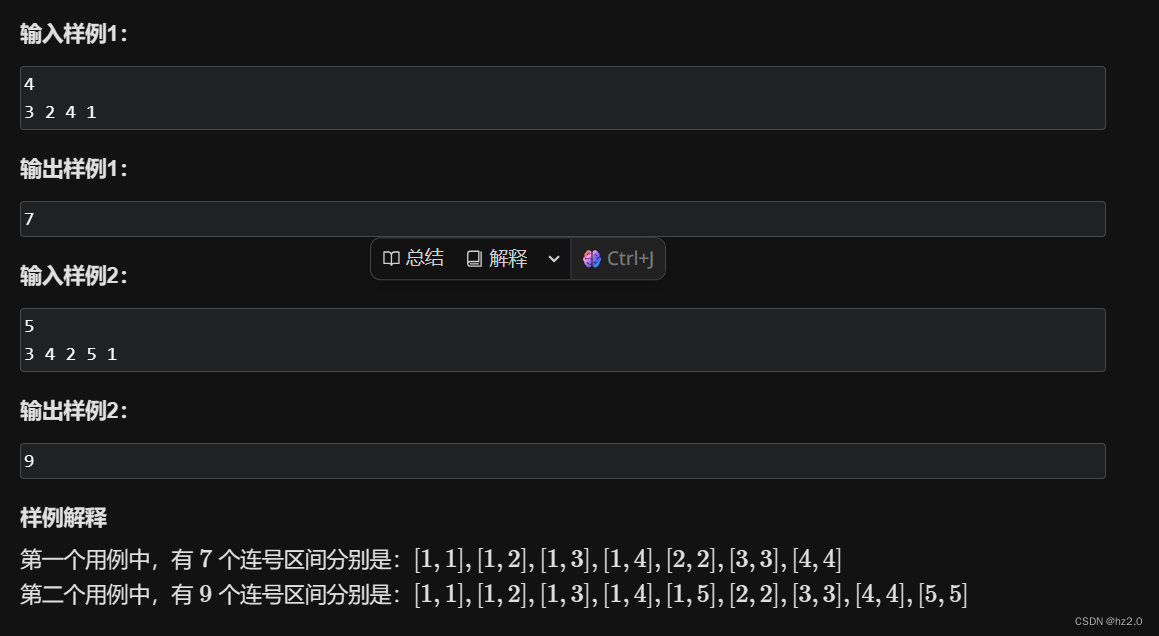
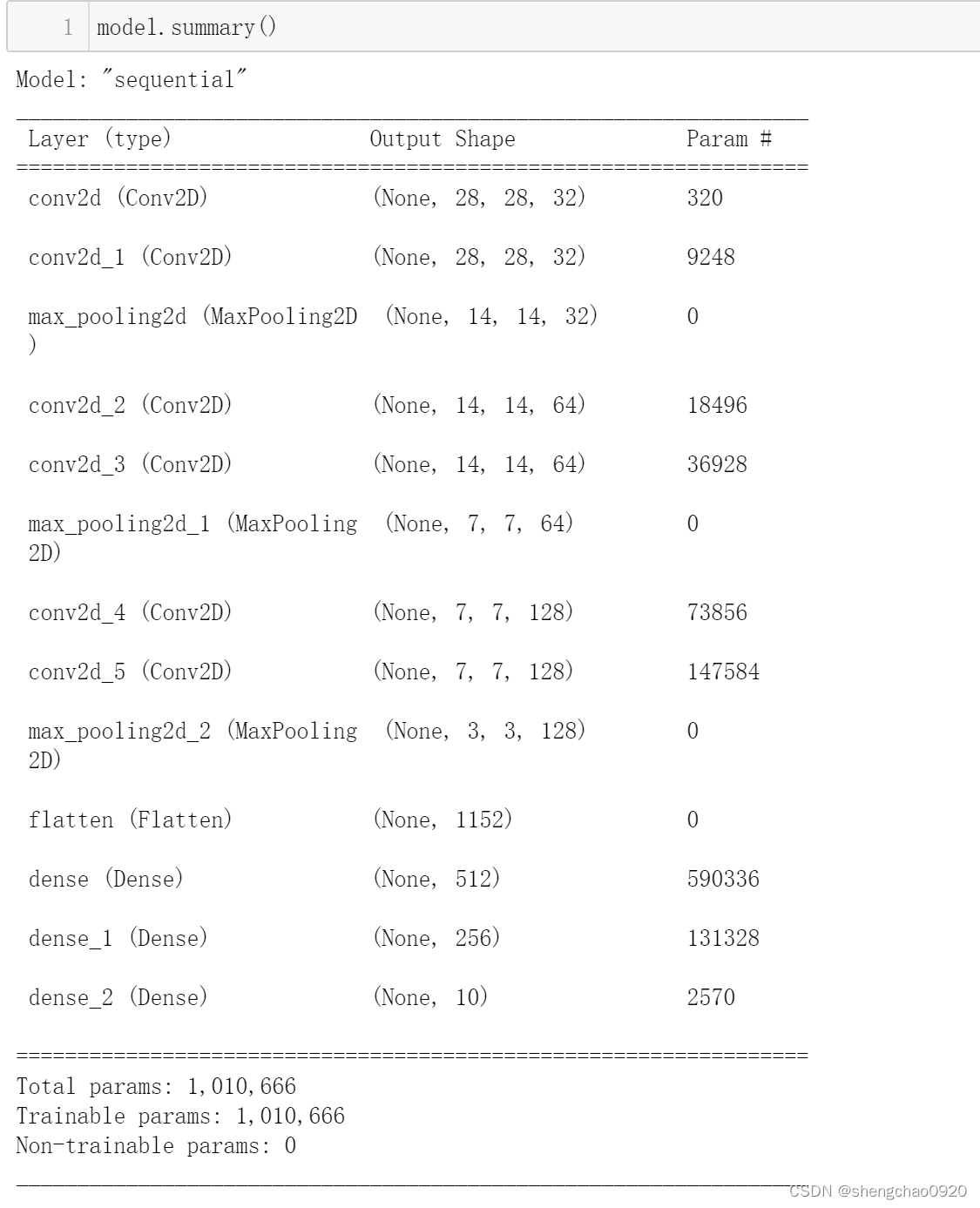
ICCV在2017年刊登了一篇经典论文《
Learning Efficient Convolutional Networks through Network Slimming》。在神经网络的卷积操作之后会得到多个特征图，通过策略突出重要的特征达到对网络瘦身的目的。在该论文中使用的剪枝策略就是稀疏化BN层中的缩放因子
。
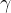BatchNorm的本质是使输入数据标准化，关于0对称，数据分布到一个量级中，在训练的时候有利于加速收敛。
BatchNorm本来公式：
在实际应用时，引入了两个可训练的参数
、
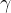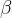。后文会详解介绍。
为什么说输入数据分布不均匀，网络分布不容易收敛，以sigmoid为例进行介绍。sigmoid函数在神经网络中常用来做激活函数，为了将非线性引入神经网络中，使得神经网络具有更加复杂的决策边界。
如sigmoid函数图像所示，输入数据在红框范围内，函数梯度较大，反向传播收敛更快。在红框外，梯度小参数更新慢，甚至有梯度消失的情况。
因此加入BN层能够很好的将数据分布规范化到均值为0，方差为1的标准正态分布。提高了激活函数的灵敏度，加速训练。
但是这样一来又引入了新的问题，我们观察红框内的函数形状类似线性函数。为了保持非线性，因此在BN中加入可训练的参数
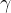和
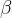来呈现非线性。
(此处不理解为什么呈现的是非线性)
改进后的BN公式：
神经网络中网络层连接顺序：conv->BN->激活层
其中，卷积层的每个通道都会对应一个缩放因子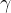，我们对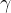小的值进行prunning，得到稀疏的网络层。
如何将重要的特征（通道）的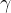值提高？ 为什么重要的特征（通道）的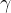值高？——使用L1正则化能对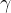进行稀疏作用。
我们先来回顾一下L1、L2正则化。
通常L1正则化用来稀疏与特征选择。目标函数通常由损失函数（此处为MSE）和正则化函数组成，L1正则项表示如下。传入的参数
经过L1正则化可以达到稀疏的效果。
L1正则化函数图像以及它的求导函数sign(θ)的图像如下。L1在反向传播，梯度更新的时候梯度下降的步长衡为1，在参数更新的时候很多参数都学成了0，因此能达到稀疏的目的。
L2正则化用来平滑特征，防止过拟合。目标函数携带L2正则项表示：
L2正则化函数及求导函数的图像：
L2求导为θ，当参数特别大时，参数更新的梯度也大，当参数特别小时，参数更新的梯度也小。因此产生平滑特征的效果。L2可以每个参数都变小但是不至于变成0，这样可以减少模型的复杂度，防止模型拟合数据中的噪声。
因此可以利用L1正则化对参数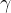进行稀疏作用。
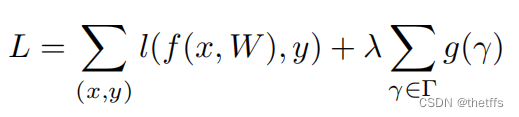
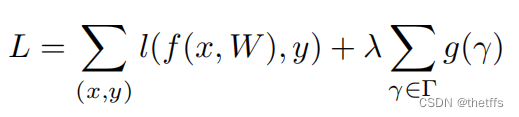
![NSS [鹏城杯 2022]压缩包](https://img-blog.csdnimg.cn/img_convert/3ddb0e3bd5a32625695fa42f07a701b1.png)
