1. 多分类SVM
1.1 基本思想
Grammer-singer多分类支持向量机的出发点是直接用超平面把样本空间划分成M个区域，其
中每个区域对应一个类别的输入。如下例，用从原点出发的M条射线把平面分成M个区域，下图画
出了M=3的情形：
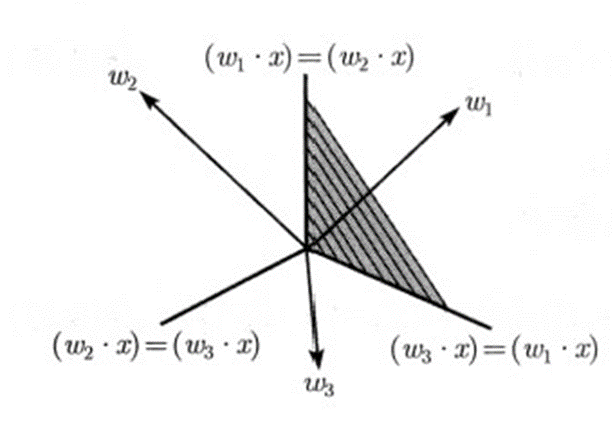
1.2 问题描述
设训练点集为：
则存在着 
使得训练点满足下式：
引进记号：
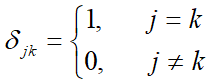
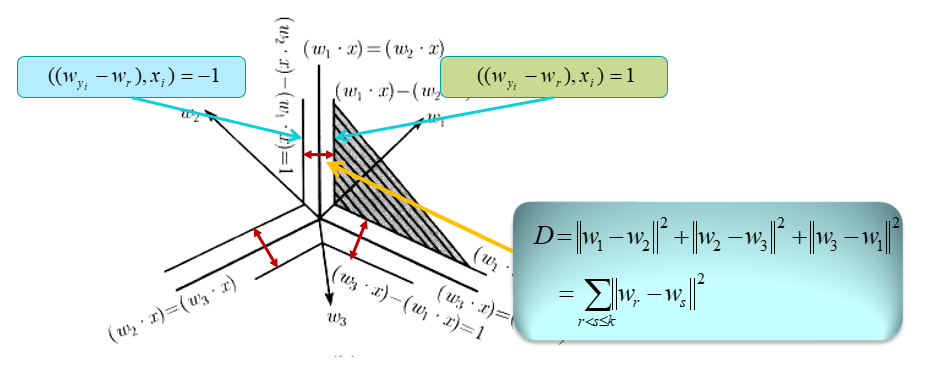
根据最大间隔原则：
其中：
，进而最优化问题可转化为：
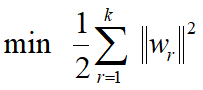
添加松弛变量：
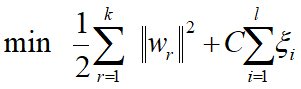
其中：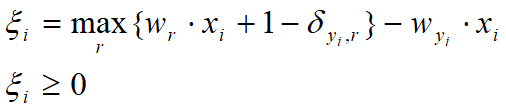
引入拉格朗日函数：
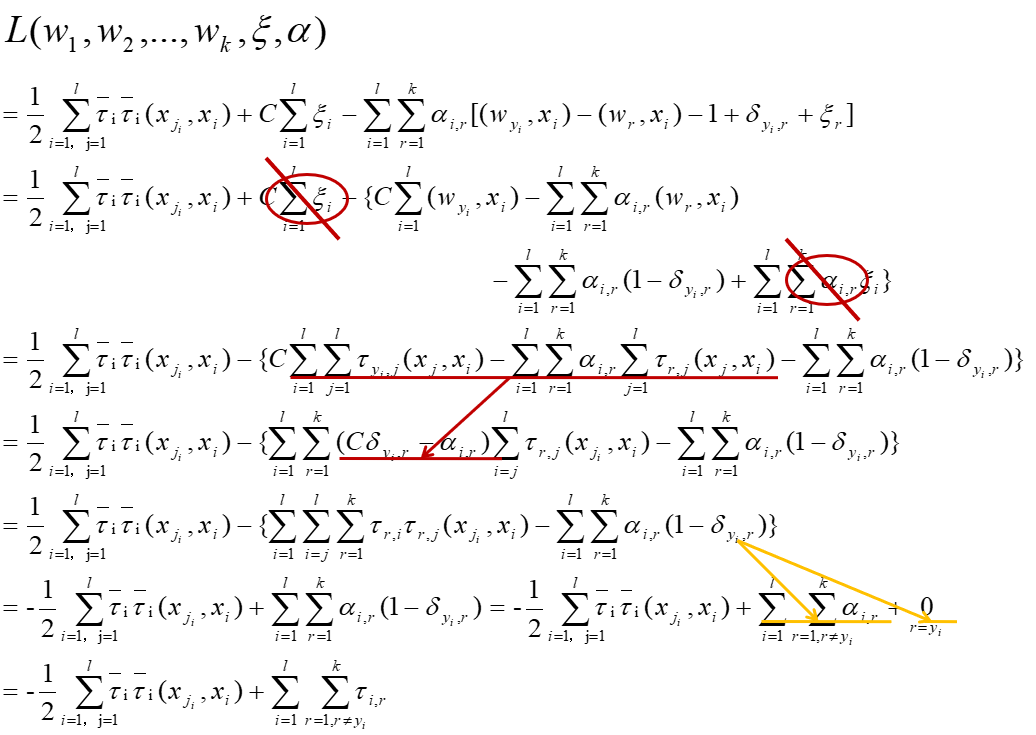
对偶函数：
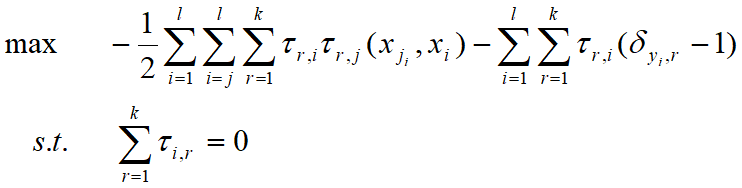样本与样本间的参数无约束
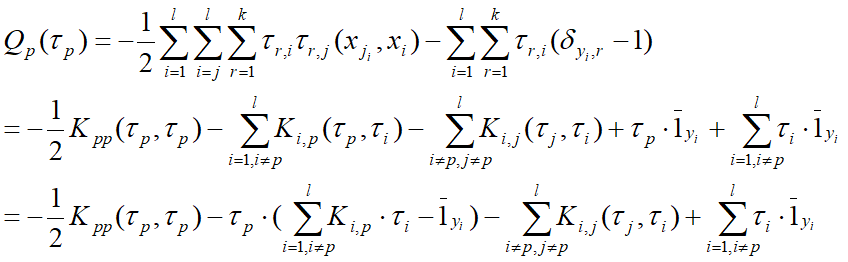
由此，进一步可优化如下目标函数：
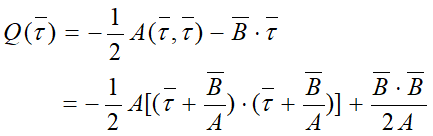其中，最后一项为常数。
带入
得到凸二次优化问题：
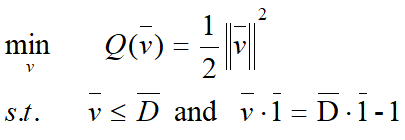
构建拉格朗日函数：
求偏导：
如果 
，那么 
；
如果 
， 那么 
，由此可得：
但有约束：
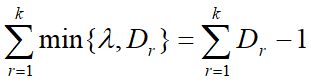
所以：
代入可得：
求解算法：
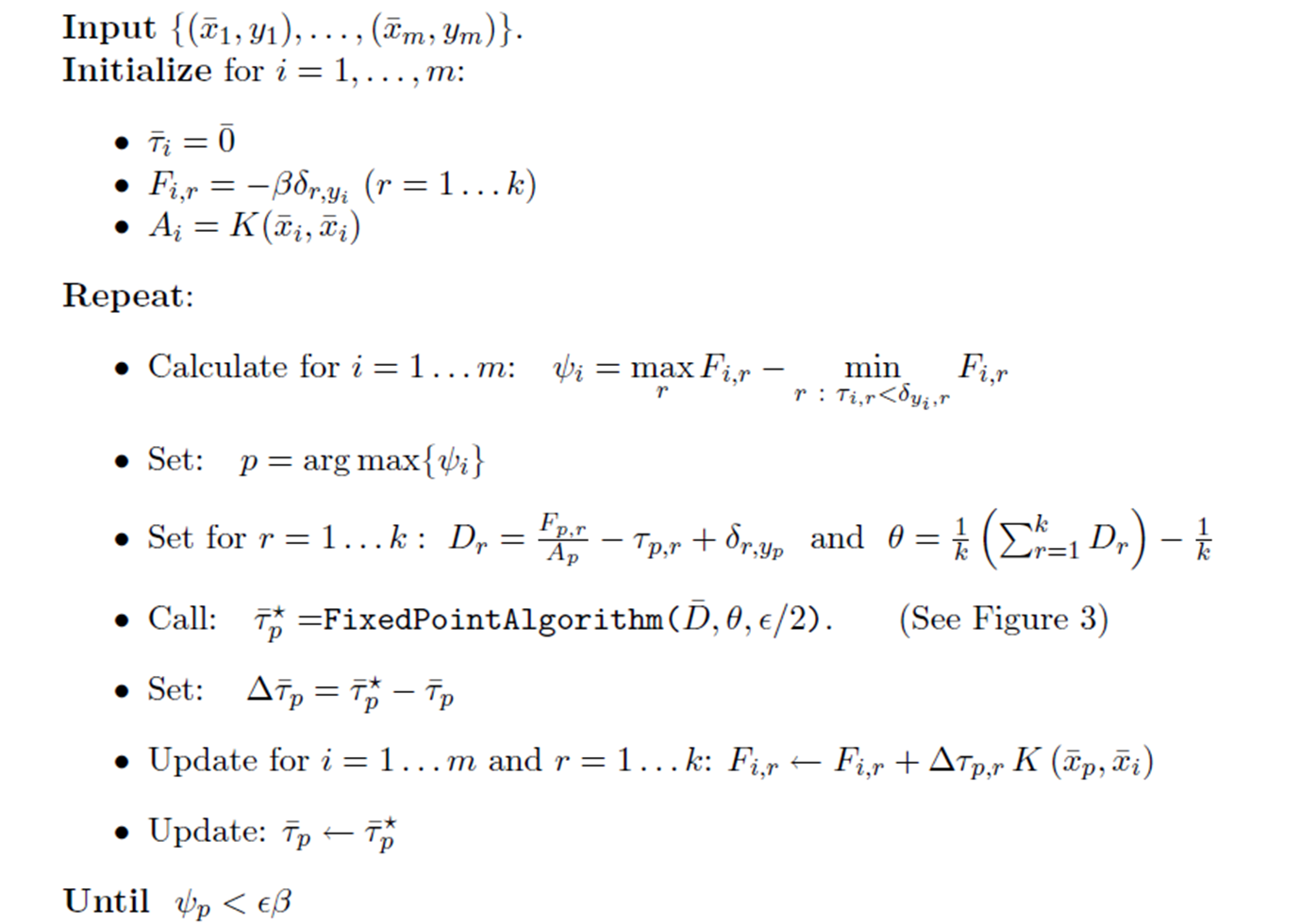
总结：这个其实是不实用的,因为将所有的sample放在一个优化函数里面，这样的训练时间非
常长，几乎无法忍受的地步，test时间还是可以的。小规模数据集可以考虑，如果数据集规模很
大，建议不要使用这个。
2. 支持向量机回归
SVM本身是针对经典的二分类问题提出的，支持向量回归机（Support Vector Regression，
SVR）是支持向量在函数回归领域的应用。SVR与SVM分类有以下不同：SVM回归的样本点只有
一类，所寻求的最优超平面不是使两类样本点分得“最开”，而是使所有样本点离超平面的“总偏差”
最小。这时样本点都在两条边界线之间，求最优回归超平面同样等价于求最大间隔。
2.1 SVR基本模型
对于线性情况，支持向量机函数拟合首先考虑用线性回归函数拟合。
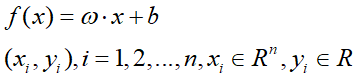
标准支持向量机采用ε -不灵敏度函数，即假设所有训练数据在精度 ε下用线性函数拟合图。
约束条件：
该问题的求解为二次优化问题，通过拉格朗日乘子转化为其对偶形式：
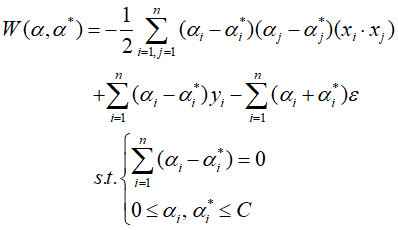
计算b的值及决策函数：
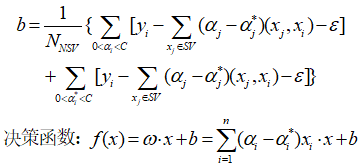
2.2 支持向量机回归--非线性
非线性SVR的基本思想是通过事先确定的非线性映射将输入向量映射的一个高维特征空间
中，然后在此高维空间中再进行线性回归，从而取得在原空间非线性回归的效果。
首先将输入量通过映射 
，映射到高维特征空间H中，则
则优化目标函数变为：
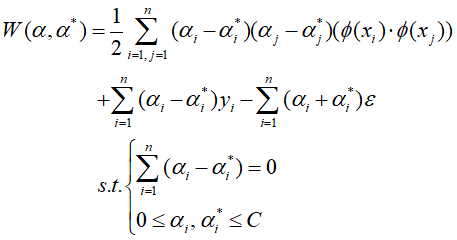
在高维空间中计算内积十分复杂，鉴于核函数优秀的内积计算性质：
则优化目标函数可表示为：
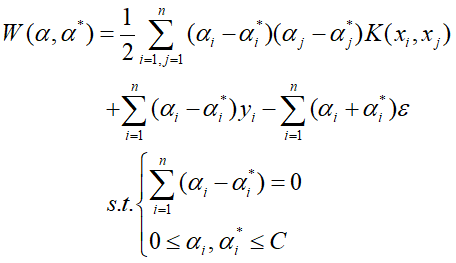
得到回归函数即为标准ε-不敏感损失函数下的回归函数形式。
可以表示为：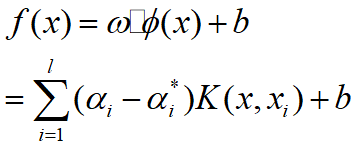 
SVM与神经网络（NN）的对比：
①SVM的理论基础比NN更坚实，更像一门严谨的“科学”（三要素：问题表示、问题解决、证明）
②SVM----严格的数学推理
③NN----强烈依赖于工程技巧
④推广能力取决于“经验风险值”和“置信范围值”，NN不能控制两者中的任何一个。
⑤NN设计者用高超的工程技巧弥补了数学上的缺陷----设计特殊的结构，利用启发式算法，有时
能得到出人意料的好结果。
