1.DQN
1.1概念
DQN相对于Q-Learning进行了三处改进：
1.引入神经网络：如下图所示希望能从状态A中提取Q(s,a)
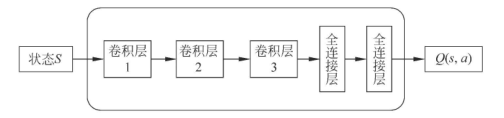
2.经验回放机制：连续动作空间采样时，前后数据具有强关联性，而神经网络训练时要求数据之间具有独立同分布特性，简单理解，就是前后输入的数据之间要有独立性，所以对于连续空间数据，采用随机采样法，
3.设置单独目标网络：下式中θ为权重参数，
为目标网络，
为目标网络和当前网络的差值，利用该误差不断更新θ。
1.2迭代过程
Q-Learning：只能解决有限维度和离散空间的任务，对于机器人控制这些高维连续空间的任务，力所不能及，之后用神经网络逼近Q（s，a；θ），也就是DQN。
DQN：值函数逼近，是逼近Q（s，a），最终目的也是得到最优Π（a|s），但又存在过优问题，所以出现了Double DQN。
Double DQN：用两个网络，如下公式所示，第一个先选择不同状态下，选择令Q(s,a)最大的动作a，然后再众多最大动作中，再由给该动作a，取一个合适的Q值，如果说
给的值也过高，那么令Q放弃该动作a，以此解决了过优问题。公式如下：
进一步人们开始思考，无论是DQN还是Double DQN，都没有考虑如何多关注贡献更大的a对应的Q,这更加符合人类学习的过程，所以引入了优势函数。
Dueling DQN：此处引入了优势函数的概念，举个例子，当我们在高速开车时，前后无车时，我们只关注状态价值V(s)即可，但遇到车时，就必须关注相应动作的价值函数值，而不同的动作对结果影响会有优劣之分，这就是动作优势。
我们都知道，状态价值函数V(s)是动作价值函数Q(s,a)的加权结果，如下图所示，在s状态下有和
两个动作值函数，加权成
，分别能得到优势函数，
和
。
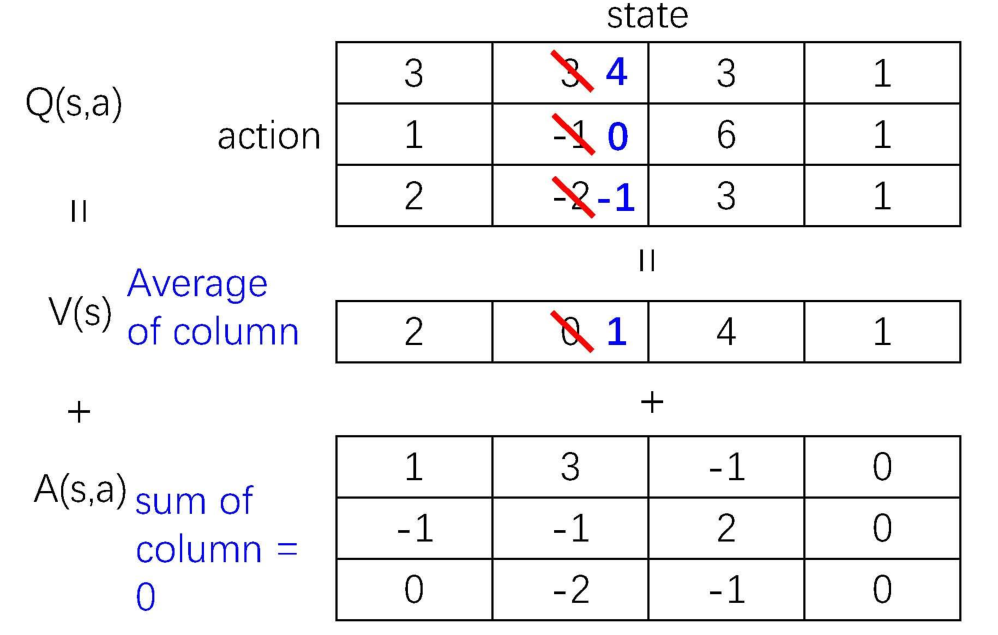
如下图所示，在进行网络训练时，DQN和Double DQN得到的是Q(s,a)，而Dueling DQN得到两个网络V(s)和A(s,a)，最终叠加得到Q(s,a)。
进一步看下图，V(s)按照Q(s,a)的平均值计算得到，然后不同的Q(s,a)-V(s)是得到不同的优势函数A(s,a)。
