算法：穷举，暴搜，深搜，回溯，剪枝

文章目录

算法基本思路
例题
- 全排列
- 子集
- 全排列II
- 电话号码和字母组合
- 括号生成
- 组合
- 目标和
- 组合总和
- 优美的排列
- N皇后
- 有效的数独
- 解数独
- 单词搜索
- 黄金矿工
- 不同路径III
总结

算法基本思路

穷举–枚举

画出决策树
设计代码

在设计代码的过程中，重点要关心到全局变量，dfs函数，和细节问题，例如有回溯，剪枝，递归出口等问题

例题

全排列

画出该全排列的决策树：

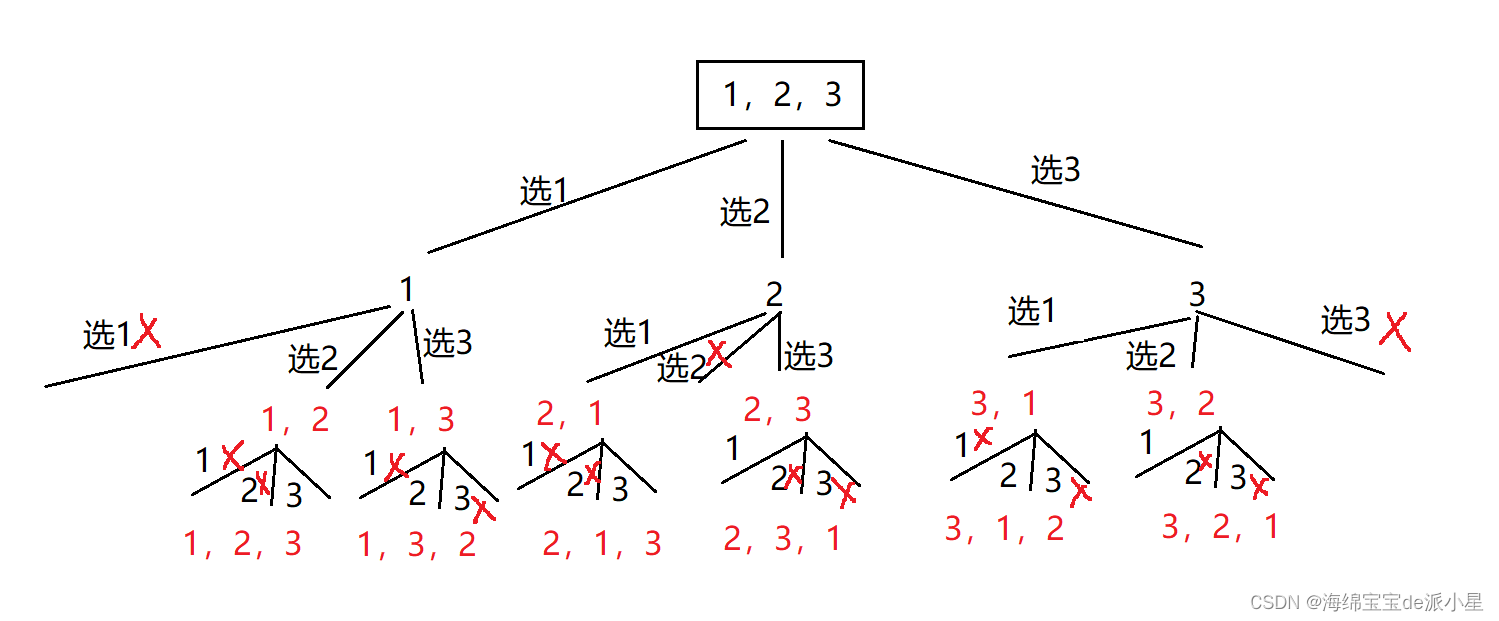
因此筛选思路也就有了，从给定的vector开始选，每选择了一个就将选的元素的下标标记为true，代表选过了，递归到下一次进行选择的时候，如果要选的元素的下标是false，代表还没有选过，就可以被选，回溯后要回复现场

class Solution 
{
public:
    // 设计全局变量
    vector<vector<int>> ret; // 返回的二维数组
    vector<int> path; // 二维数组中的元素
    bool check[7]; // 判断元素是否被统计过了
    
    void dfs(vector<int>& nums)
    {
        // 递归出口
        if(path.size() == nums.size())
        {
            ret.push_back(path);
            return;
        }

        for(int i=0;i<nums.size();i++)
        {
            // 如果该字符没有被统计过就进行统计
            if(check[i] == false)
            {
                path.push_back(nums[i]);
                check[i] = true;
                // 进入递归
                dfs(nums);
                // 回溯和恢复现场
                path.pop_back();
                check[i] = false;
            }
        }
    }

    vector<vector<int>> permute(vector<int>& nums) 
    {
        dfs(nums);
        return ret;
    }
};

子集

对于这个题有两种决策方案：
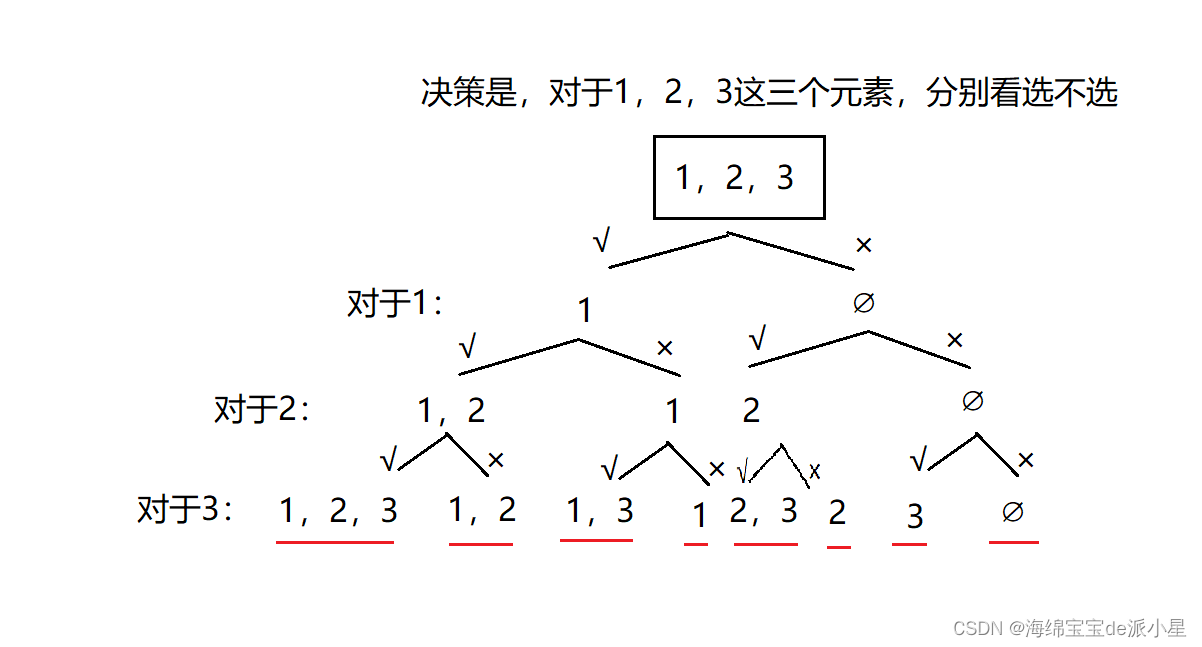
第一种决策方案是，对于nums数组中的每一个元素，都看它是否需要被选，可以选择要被选，也可以选择不被选
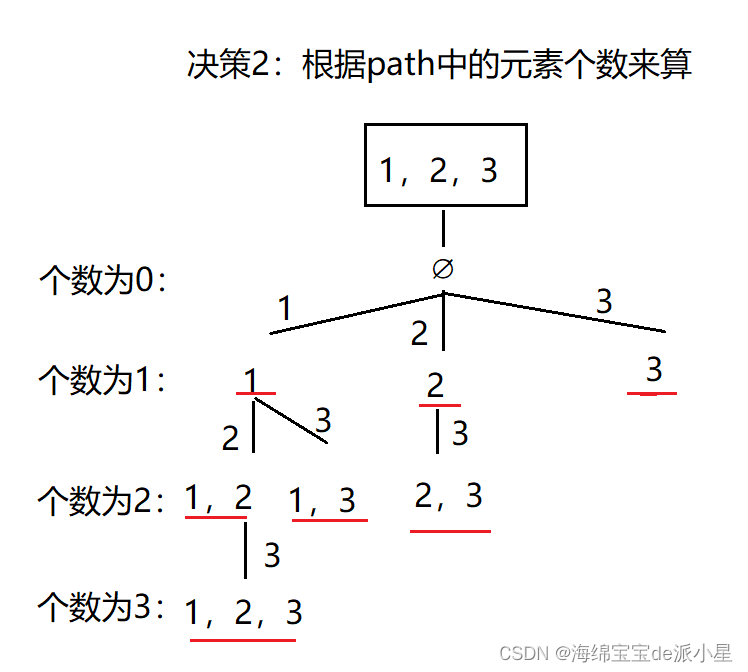
第二种决策方案是，对于path数组中的元素个数，可以为一个，也可以为两个，也可以为三个，直到和nums数组中元素的个数一样

决策1：

class Solution 
{
public:
    vector<vector<int>> ret; // 返回值
    vector<int> path; // 数组中的元素

    void dfs(vector<int>& nums, int pos)
    {
        for(int i=pos;i<nums.size();i++)
        {
            // 选
            path.push_back(nums[i]);
            dfs(nums,i+1);

            // 不选
            path.pop_back();
        }
        ret.push_back(path);
    }

    vector<vector<int>> subsets(vector<int>& nums) 
    {
        dfs(nums,0);
        return ret;
    }
};

决策2：

class Solution 
{
public:
    vector<vector<int>> ret; // 返回值
    vector<int> path; // 数组中的元素

    void dfs(vector<int>& nums, int pos)
    {
        ret.push_back(path);
        for(int i=pos;i<nums.size();i++)
        {
            // 数组中元素的个数
            path.push_back(nums[i]);
            dfs(nums,i+1);
            // 回溯+恢复现场
            path.pop_back();
        }
    }

    vector<vector<int>> subsets(vector<int>& nums) 
    {
        dfs(nums,0);
        return ret;
    }
};

全排列II

前面有做过一道全排列，这个题和前面题的不同点就是多了相同元素，因此对于剪枝的策略有不同，下面首先画出它的决策树

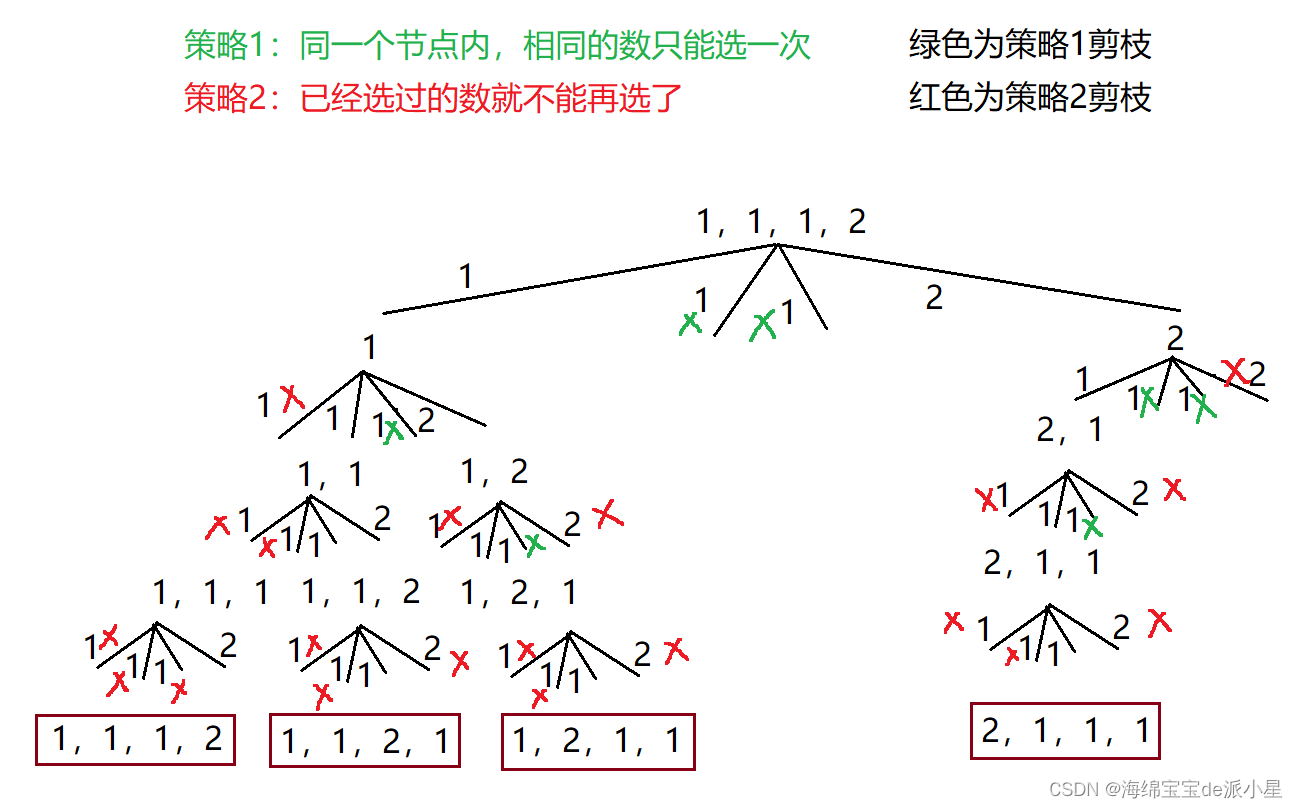
从决策树中可以看出这个题的剪枝方案

在同一个节点，相同的数不能被选两次 — 比较这个数有没有被选过
在不同的节点，已经被选过的数就不能被选了 — check数组

class Solution 
{
public:
    // 设计全局变量
    vector<vector<int>> ret;
    vector<int> path;
    bool check[9];

    void dfs(vector<int>& nums)
    {
        // 递归终止条件
        if(path.size() == nums.size())
        {
            ret.push_back(path);
            return;
        }

        for(int i = 0; i < nums.size(); i++)
        {
            // 剪枝的条件：当前节点没用过并且前面没出现过
            if(check[i] == false && (i == 0 || nums[i] != nums[i-1] || check[i-1]))
            {
                path.push_back(nums[i]);
                check[i] = true;
                dfs(nums);
                // 回溯
                check[i] = false;
                path.pop_back();
            }
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) 
    {
        sort(nums.begin(),nums.end());
        dfs(nums);
        return ret;
    }
};

电话号码和字母组合

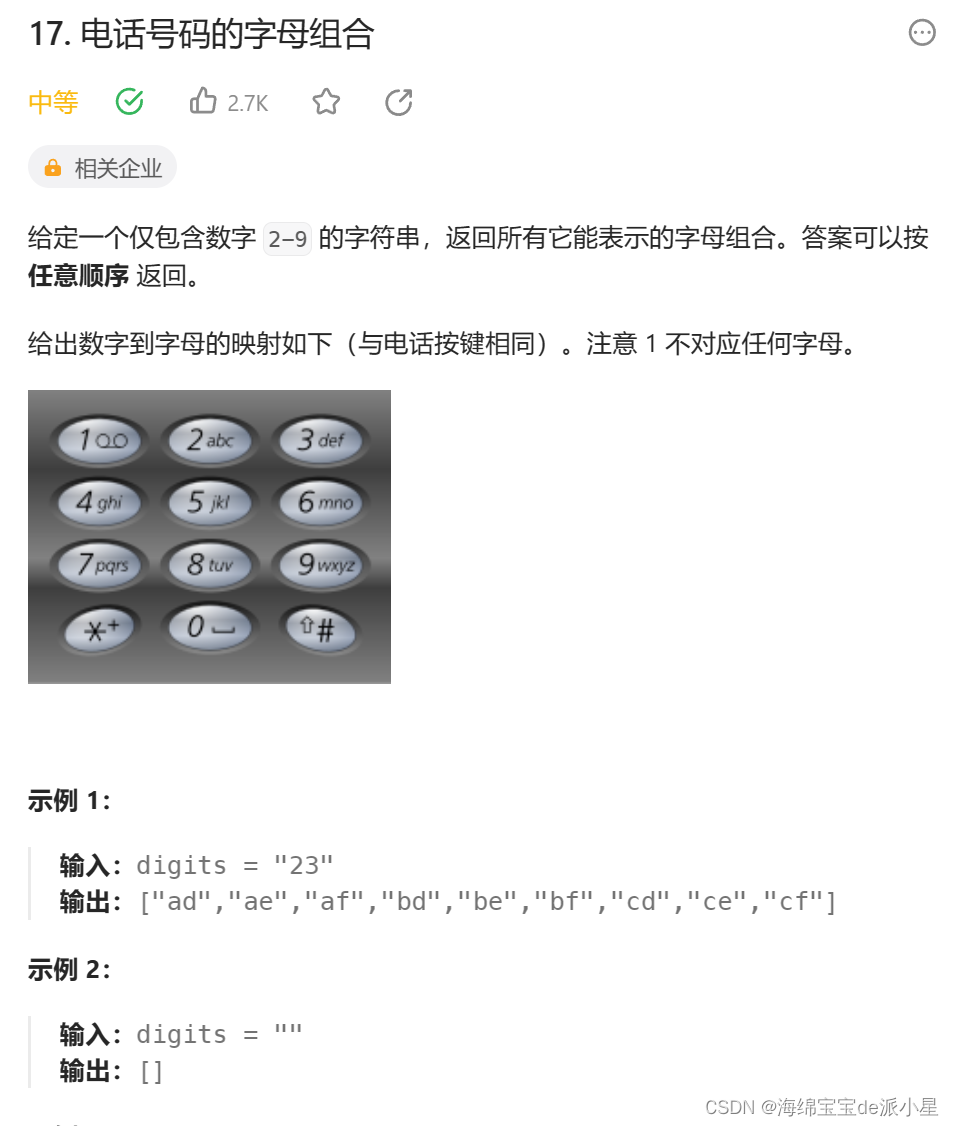
class Solution 
{
public:
    // 全局变量
    string arr[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    vector<string> ret;
    string path;

    // 决策：取digits中每一个数字对应的字符串中的元素，直接取即可
    void dfs(string& digits, int pos)
    {
        // 递归终止条件
        if(path.size() == digits.size())
        {
            ret.push_back(path);
            return;
        }

        for(auto e : arr[digits[pos] - '0'])
        {
            path += e;
            dfs(digits, pos+1);
            // 回溯+恢复现场
            path.pop_back();
        }
    }

    vector<string> letterCombinations(string digits) 
    {
        if(digits.size() == 0)
            return ret;
        dfs(digits, 0);
        return ret;
    }
};

括号生成

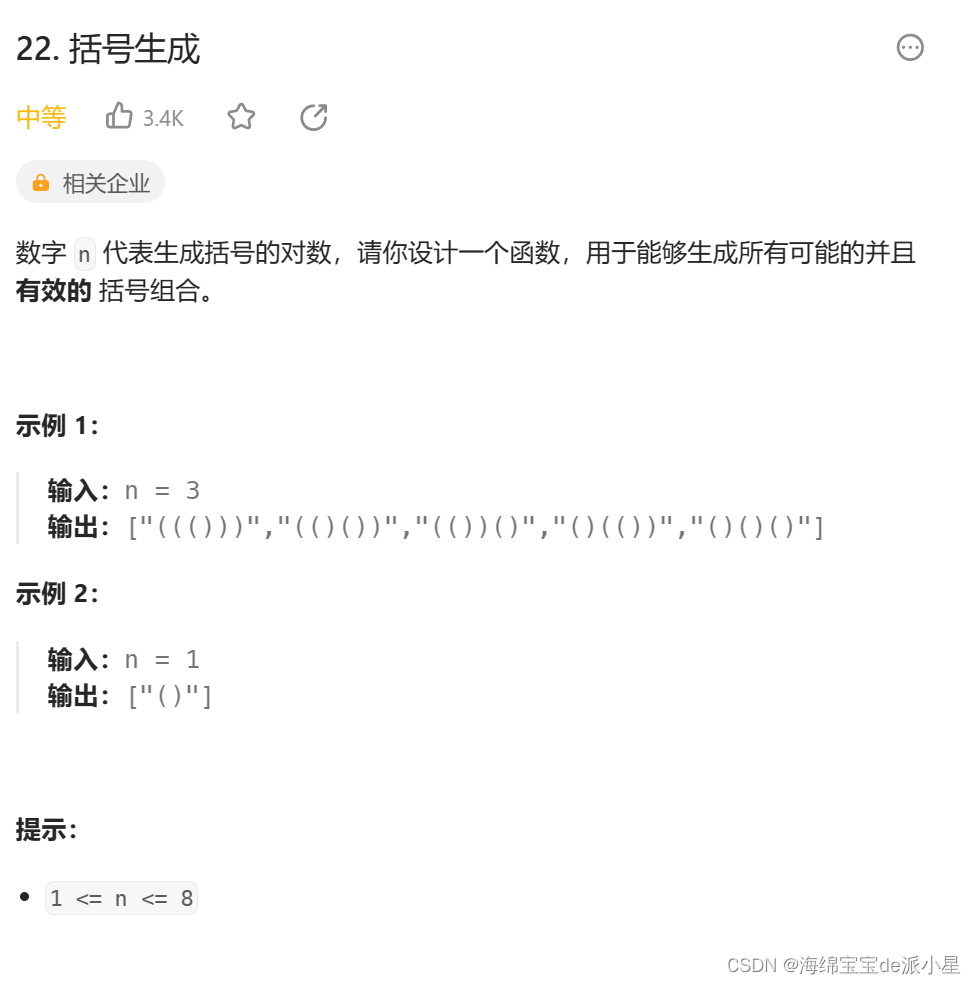
首先画出这个题的决策树，观察决策树的剪枝情况

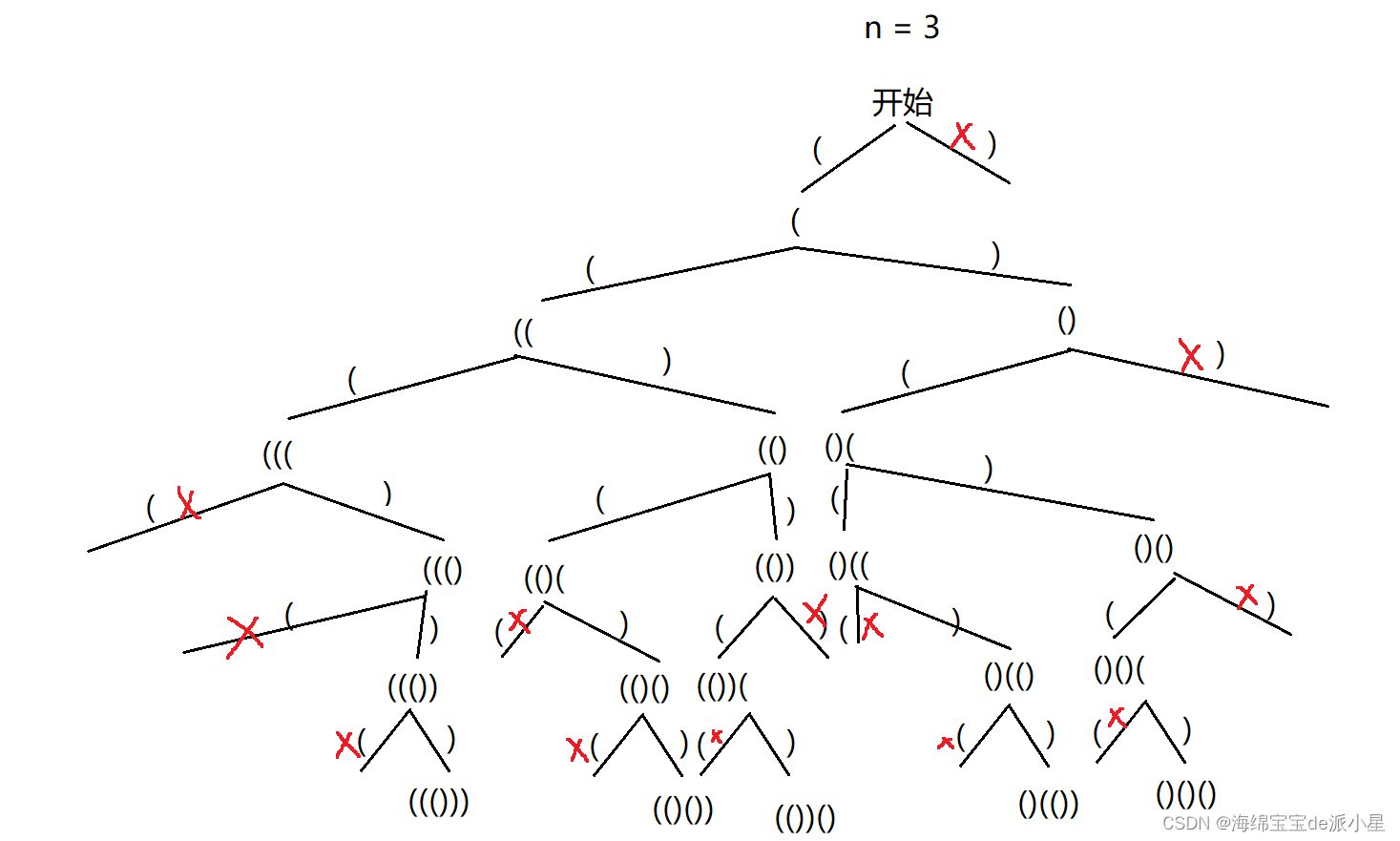
从中可以看出，这个题的剪枝条件是，右括号的数量不能大于左括号的数量，并且左括号的数量不能大于n

全局变量如何设计？答案存储在一个数组中，每一个path也要有一个字符串用以描述

递归函数头如何设计？首先必须要知道n是多少，其次要知道左括号现在有多少，右括号现在有多少

递归函数的实现细节：递归终止条件是path的长度等于n的2倍，回溯要将最后插入的部分删除掉

因此函数就很好实现了：

class Solution
{
public:
    vector<string> res;
    string path;

    void dfs(int n, int left, int right)
    {
        // 递归终止条件
        if (path.size() == n * 2)
        {
            res.push_back(path);
            return;
        }

        // 添加左括号的剪枝条件
        if (left < n)
        {
            path += '(';
            left++;
            dfs(n, left, right);
            // 回溯+恢复现场
            path.pop_back();
            left--;
        }
        // 添加右括号的剪枝条件
        if (left > right)
        {
            path += ')';
            right++;
            dfs(n, left, right);
            // 回溯+恢复现场
            path.pop_back();
            right--;
        }
    }

    vector<string> generateParenthesis(int n)
    {
        dfs(n, 0, 0);
        return res;
    }
};

组合

画出决策树

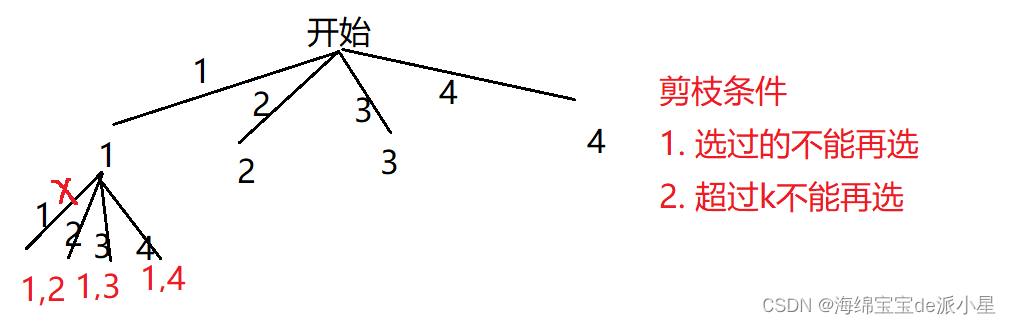
这里要注意这两个条件，其实在代码中是不需要专门体现的，首先，选过的不能再选，也就是说子集的元素都是升序排列的，那么只需要在递归的时候直接从当前位置的下一个位置开始找数即可

check数组的存在意义？

通过这个题，对于check数组有了更多的理解，check数组存在的意义是，选完一个数后，在选第二个数的过程中，需要从头再次开始选的时候，为了避免会重复选用，因此会有check数组来用以标记，但是在这个题中，选了一个数以后，选第二个数直接从这个数的下一个数开始选就可以了，因此实际上是不需要check数组来帮忙的

class Solution
{
public:
	// 定义全局变量
	vector<vector<int>> ret;
	vector<int> path;
	bool check[25];

	void dfs(int n, int k, int pos)
	{
		// 递归终止条件
		if (path.size() == k)
		{
			ret.push_back(path);
			return;
		}

		for (int i = pos; i <= n; i++)
		{
			path.push_back(i);
			dfs(n, k, i + 1);
			// 回溯+恢复现场
			path.pop_back();
		}
	}

	vector<vector<int>> combine(int n, int k)
	{
		dfs(n, k, 1);
		return ret;
	}
};

目标和

首先画出它的决策树，从中可以看出它和子集的那道题有异曲同工之处，在此基础上，对这个决策树进行实现

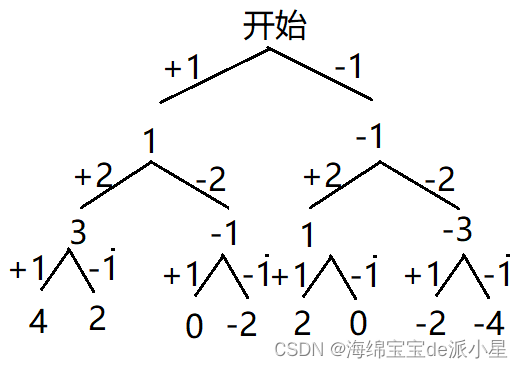
class Solution
{
public:
	// 定义全局变量
	int count;
	void dfs(vector<int>& nums, int target, int pos, int path)
	{
		if (pos == nums.size())
		{
			if (path == target)
				count++;
			return;
		}
		dfs(nums, target, pos + 1, path + nums[pos]);
		dfs(nums, target, pos + 1, path - nums[pos]);
	}
	int findTargetSumWays(vector<int>& nums, int target)
	{
		dfs(nums, target, 0, 0);
		return count;
	}
};

组合总和

决策树

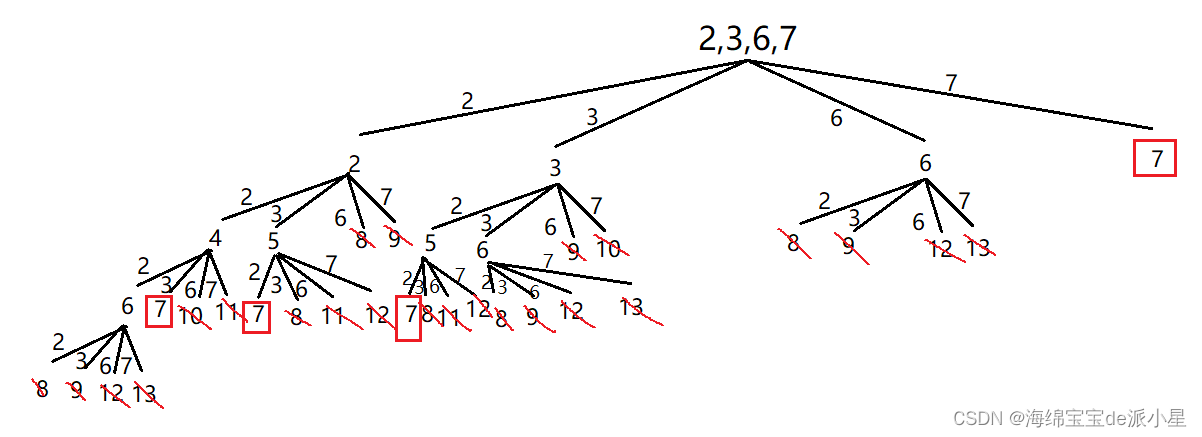
如果在不考虑去重的情况下，这样的决策树是可以的，但是这里题目要求有要去重的阶段，因此就需要考虑剪枝的问题

如何剪枝？

对于数据的选择，如果先选了2，再选3，那么在选3的时候就不应该再选2，因此剪枝的策略就是选的时候不选前面的，因为如果前面的能选，那么在前面选的时候一定选了后面的，所以只需要向前进行寻找即可，不用管后面的部分

这样的决策树才理应是正确的决策树

class Solution 
{
public:
    // 定义全局变量
    vector<vector<int>> ret;
    vector<int> path;

    void dfs(vector<int>& candidates, int target, int pos, int sum)
    {
        // 递归终止条件
        if(sum == target)
        {
            ret.push_back(path);
            return;
        }
        if(sum > target)
            return;

        for(int i = pos; i < candidates.size(); i++)
        {
            path.push_back(candidates[i]);
            dfs(candidates, target, i, sum + candidates[i]);
            // 回溯+恢复现场
            path.pop_back();
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) 
    {
        dfs(candidates, target, 0, 0);
        return ret;
    }
};

这是其中一种决策方案，下面提供决策的第二种思路

在数据选择方面，假设现在有2,3,5三个数字，可以对其中的每个数字选不同的次数，例如选0次，1次，2次…

优美的排列

一开始第一反应是，先把数组搞出来，再进行判断，但这样会超时，意味着有些地方需要被优化

// 超时
class Solution 
{
    // 思路：全排列出来数据，然后判断是否优美
public:
    // 全局变量
    bool check[20];
    vector<int> path;
    int count;

    bool check_perm(const vector<int>& nums)
    {
        for(int i = 0; i < nums.size(); i++)
        {
            if(max(nums[i],i+1) % min(nums[i],i+1) != 0)
                return false;
        }
        return true;
    }

    void dfs(int n)
    {
        // 递归终止条件
        if(path.size() == n)
        {
            if(check_perm(path)) count++;
            return;
        }
        for(int i = 0; i < n; i++)
        {
            if(check[i] == false)
            {
                path.push_back(i + 1);
                check[i] = true;
                dfs(n);
                // 回溯现场
                path.pop_back();
                check[i] = false;
            }
        }
    }

    int countArrangement(int n) 
    {
        dfs(n);
        return count;
    }
};

N皇后

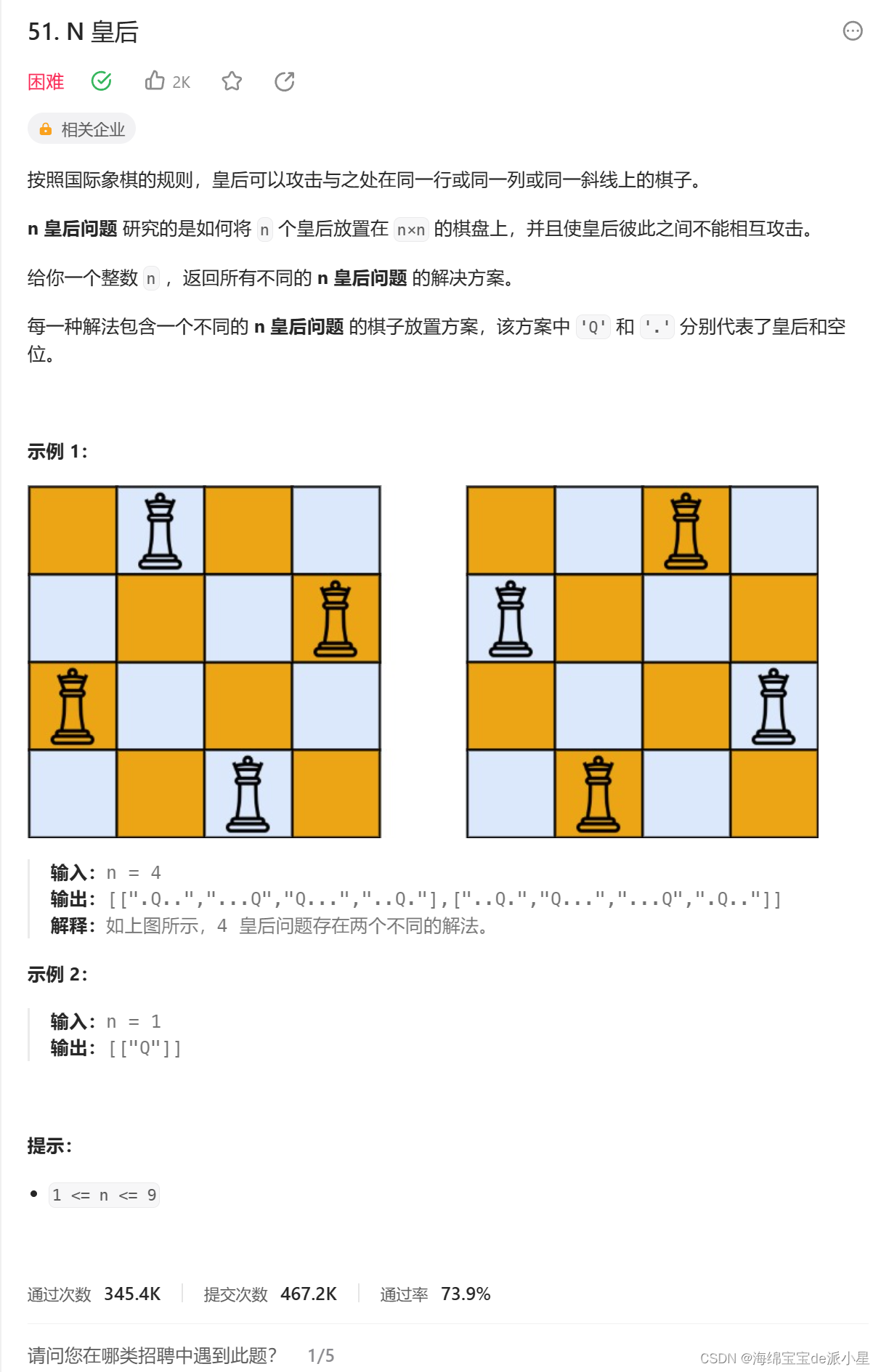
关于check判断，还可以使用类似于哈希表的解法，在下一道题中进行使用

class Solution
{
public:
    // 全局变量
    int _n;
    vector<vector<string>> ret;
    vector<string> path;

    // 构建皇后摆放情况
    string con_string(int pos, int n)
    {
        string tmp;
        for (int i = 0; i < pos; i++)
            tmp += '.';
        tmp += 'Q';
        while (tmp.size() != n)
            tmp += '.';
        return tmp;
    }

    // 判断能不能在第i行的pos位置放置皇后
    bool check(int i, int pos)
    {
        // 判断列
        for (int j = 0; j < i; j++)
        {
            if (path[j][pos] == 'Q')
                return false;
        }
        // 判断主对角线
        for (int j = 1; i - j >= 0 && pos + j < _n; j++)
        {
            if (path[i - j][pos + j] == 'Q')
                return false;
        }
        // 判断次对角线
        for (int j = 1; i - j >= 0 && pos - j >= 0; j++)
        {
            if (path[i - j][pos - j] == 'Q')
                return false;
        }
        return true;
    }

    void dfs(int n, int pos)
    {
        // 终止条件
        if (pos == n)
        {
            ret.push_back(path);
            return;
        }

        for (int i = 0; i < n; i++)
        {
            // 剪枝判断pos行的i位置是否可以放皇后，如果成功就放到棋盘中
            if (check(pos,i))
            {
                // 构建出当前皇后摆放情况
                string tmp = con_string(i, n);
                path.push_back(tmp);
                // 递归到下一层去判断
                dfs(n, pos + 1);
                // 回溯 恢复现场
                path.pop_back();
            }
        }
    }

    vector<vector<string>> solveNQueens(int n)
    {
        _n = n;
        dfs(n, 0);
        return ret;
    }
};

有效的数独

此题就是利用了类似哈希表的方法

class Solution 
{
public:
    // 利用哈希表的原理来解题
    // 全局变量:col/row[i][j]表示第i行/列中j元素是否出现过，grid是把每个九宫格当成一个元素
    bool col[9][10];
    bool row[9][10];
    bool grid[3][3][10];
    bool isValidSudoku(vector<vector<char>>& board) 
    {
        for(int i = 0; i < board.size(); i++)
        {
            for(int j = 0; j < board[i].size(); j++)
            {
                if(board[i][j] == '.') continue;
                
                if(col[i][board[i][j] - '0'] == false)
                {
                    col[i][board[i][j] - '0'] = true;
                }
                else
                {
                    return false;
                }

                if(row[j][board[i][j] - '0'] == false)
                {
                    row[j][board[i][j] - '0'] = true;
                }
                else
                {
                    return false;
                }

                if(grid[i / 3][j / 3][board[i][j] - '0'] == false)
                {
                    grid[i / 3][j / 3][board[i][j] - '0'] = true;
                }
                else
                {
                    return false;
                }
            }
        }
        return true;
    }
};

解数独

解决本题需要依赖前面的思想


class Solution 
{
public:
    // 全局变量
    bool col[9][10];
    bool row[9][10];
    bool grid[3][3][10];

    void solveSudoku(vector<vector<char>>& board) 
    {
        for(int i = 0; i < 9; i++)
        {
            for(int j = 0; j < 9; j++)
            {
                if(board[i][j] != '.')
                {
                    col[j][board[i][j] - '0'] = true;
                    row[i][board[i][j] - '0'] = true;
                    grid[i / 3][j / 3][board[i][j] - '0'] = true;
                }
            }
        }
        dfs(board);
    }

    bool dfs(vector<vector<char>>& board)
    {
        // 构造行和列
        for(int i = 0; i < 9; i++)
        {
            for(int j = 0; j < 9; j++)
            {
                if(board[i][j] == '.')
                {
                    for(int num = 1; num <= 9; num++)
                    {
                        // 剪枝
                        if(!row[i][num] && !col[j][num] && !grid[i / 3][j / 3][num])
                        {
                            board[i][j] = num + '0';
                            row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
                            if(dfs(board) == true)
                                return true;
                            // 回溯+恢复现场
                            board[i][j] = '.';
                            row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = false;
                        }
                    }
                    return false;
                }
            }
        }
        return true;
    }
};

单词搜索

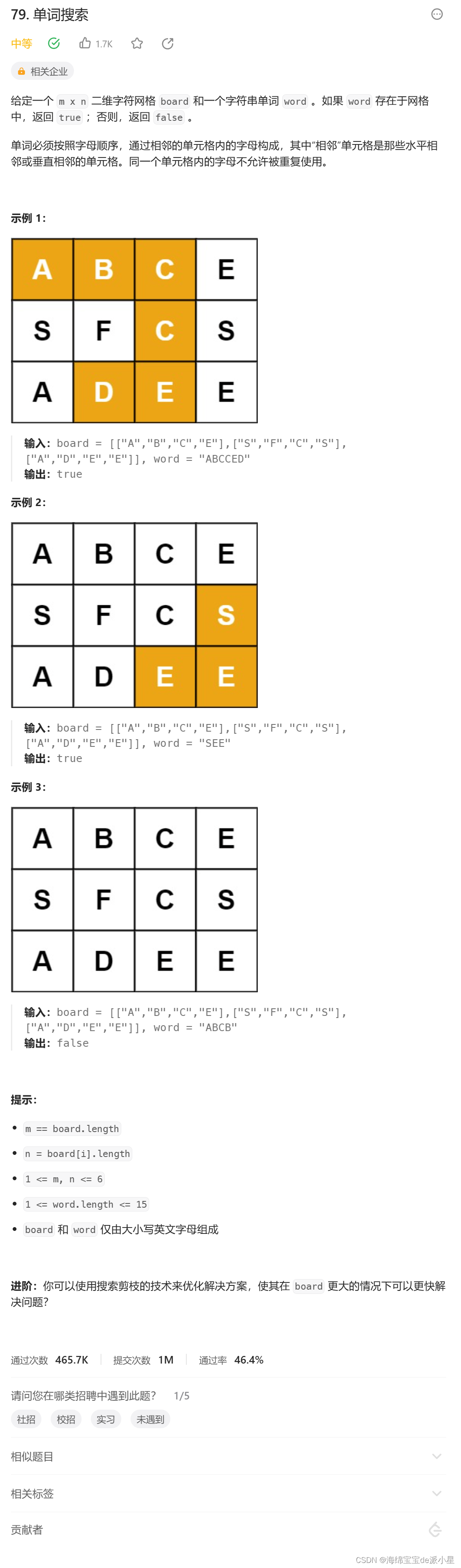
本题是使用的是矩阵中的搜索，有些类似于迷宫问题

其中需要注意的是在判断上下左右是否有内容的时候，要使用的是一个向量来标记，这样就可以避免写四层循环带来的代码冗余，在解决矩阵搜索的内容中这样的方法很方便使用

class Solution
{
public:
	// 全局变量 m为行数，n为列数
	int m;
	int n;
	string target;
	bool status;
	string path;
	bool check[7][7];
    int dx[4] = {0, 0, -1, 1};
    int dy[4] = {1, -1, 0, 0};

	// pos代表的是现在正在寻找的元素对应的下标
	void dfs(vector<vector<char>>& board, int p, int q, int pos)
	{
		if (pos == target.size())
		{
			status = true;
			return;
		}
		// 去这个格子上下左右进行寻找
        for(int i = 0; i < 4; i++)
        {
            int row = p + dx[i];
            int col = q + dy[i];
            if (row < m && row >= 0 && col < n && col >= 0 && board[row][col] == target[pos] && check[row][col] == false)
            {
                // 说明找到了，到下一层去找找
                check[row][col] = true;
                path.push_back(board[row][col]);
                dfs(board, row, col, pos + 1);
                // 回溯 恢复现场
                check[row][col] = false;
                path.pop_back();
            }
        }
	}

	bool exist(vector<vector<char>>& board, string word)
	{
		m = board.size();
		n = board[0].size();
		target = word;
		// 此时说明已经找到了target[0]，于是可以继续寻找
		path.push_back(target[0]);
		for (int i = 0; i < board.size() && status == false; i++)
		{
            for(int j = 0; j< board[i].size(); j++)
            {
                if(board[i][j] == target[0])
                {
                    check[i][j] = true;
                    dfs(board, i, j, 1);
                    check[i][j] = false;
                }
            }
		}
		return status == true;
	}
};

黄金矿工

策略：找到有黄金的格子，从这个格子开始进行深度优先遍历，每次遍历到找不见路就停止，中间记录黄金数

class Solution
{
	// 策略：找到有黄金的格子，从这个格子开始进行深度优先遍历，每次遍历到找不见路就停止，中间记录黄金数
public:
	// 全局变量
	int res;  // 获得黄金最多的数量
	bool check[16][16];  // 判断这个格子有没有走过
	// 定义偏移量
	int dx[4] = { 0, 0, 1, -1 };
	int dy[4] = { 1, -1, 0, 0 };

	// 从第i行第j列开始开采，开采量是path
	void dfs(vector<vector<int>>& grid, int i, int j, int path)
	{
		res = max(res, path);
		for (int k = 0; k < 4; k++)
		{
			int x = dx[k] + i, y = dy[k] + j;
			// 剪枝 如果这个格子有矿并且没有被走过
			if (x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size() && grid[x][y] != 0 && check[x][y] == false)
			{
				check[x][y] = true;
				dfs(grid, x, y, path + grid[x][y]);
				// 回溯和恢复现场
				check[x][y] = false;

			}
		}
	}

	int getMaximumGold(vector<vector<int>>& grid)
	{
		for (int i = 0; i < grid.size(); i++)
		{
			for (int j = 0; j < grid[i].size(); j++)
			{
				if (grid[i][j] != 0)
				{
					// 标记该处已经被开采了
					check[i][j] = true;
					// 从i j开始开采，开采量是grid[i][j]
					dfs(grid, i, j, grid[i][j]);
					// 回溯和恢复现场
					check[i][j] = false;
				}
			}
		}
		return res;
	}
};

不同路径III

class Solution 
{
public:
    bool check[21][21];
    int ret;
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    int step;

    void dfs(vector<vector<int>>& grid, int i, int j, int count)
    {
        if(grid[i][j] == 2)
        {
            if(count == step)
                ret++;
            return;
        }

        for(int k = 0; k < 4; k++)
        {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size() && grid[x][y] != -1 && check[x][y] == false)
            {
                check[x][y] = true;
                dfs(grid, x, y, count + 1);
                check[x][y] = false;
            }
        }
    }

    int uniquePathsIII(vector<vector<int>>& grid) 
    {
        int x, y;
        for(int i = 0; i < grid.size(); i++)
        {
            for(int j = 0; j < grid[0].size(); j++)
            {
                if(grid[i][j] == 1)
                {
                    x = i;
                    y = j;
                }
                else if(grid[i][j] == 0)
                {
                    step++;
                }
            }
        }
        step += 2;
        check[x][y] = true;
        dfs(grid, x, y, 1);
        return ret;
    }
};