文章目录
- 前言
- 一、线性调频信号的形式
- 1、原理
- 2、时域表达式
- 3、频域表达式
- 二、MATLAB 仿真
- 1、涅菲尔积分
- ①、MATLAB 源码
- ②、仿真结果
- 2、LFM
- ①、MATLAB 源码
- ②、仿真结果
- 1) 典型 LFM 波形,实部
- 2) 典型 LFM 波形,虚部
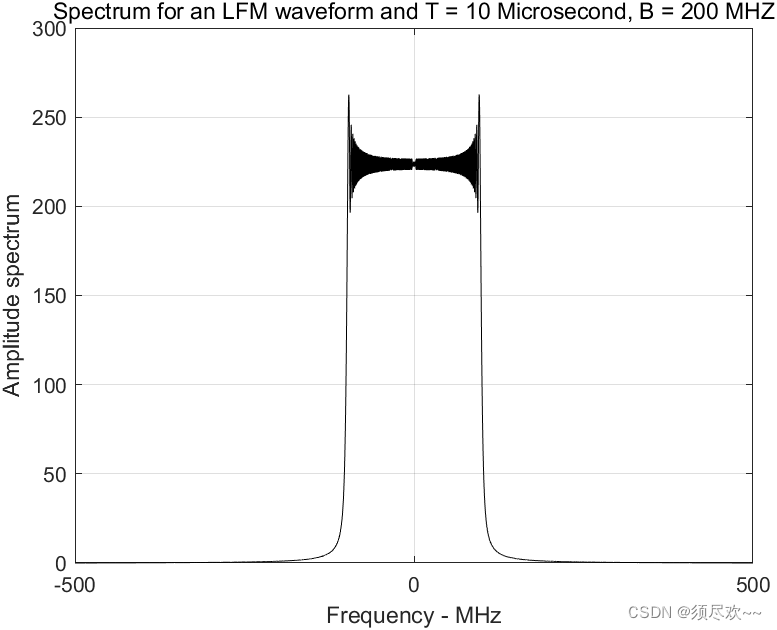
- 3) LFM 波形的典型谱
前言
线性调频(Linear Frequency Modulation,LFM)信号具有很大的时宽带宽积,可获得很大的脉冲压缩比,是雷达系统和声呐系统广泛采用的一种信号形式。本文主要进行线性调频信号的理论学习,并使用 MATLAB 进行仿真。
一、线性调频信号的形式
1、原理
频率或相位调制信号用来得到宽得多的工作带宽。线性调频(LFM)是常用的方式。在这种情况下,频率在脉宽内线性扫描,或者向上(上调频)或者向下(下调频)。匹配滤波器的带宽与扫描的带宽成比例,与脉宽无关,下图为一个典型的 LFM 波形样本,脉宽为
τ
\tau
τ,带宽为
B
B
B。
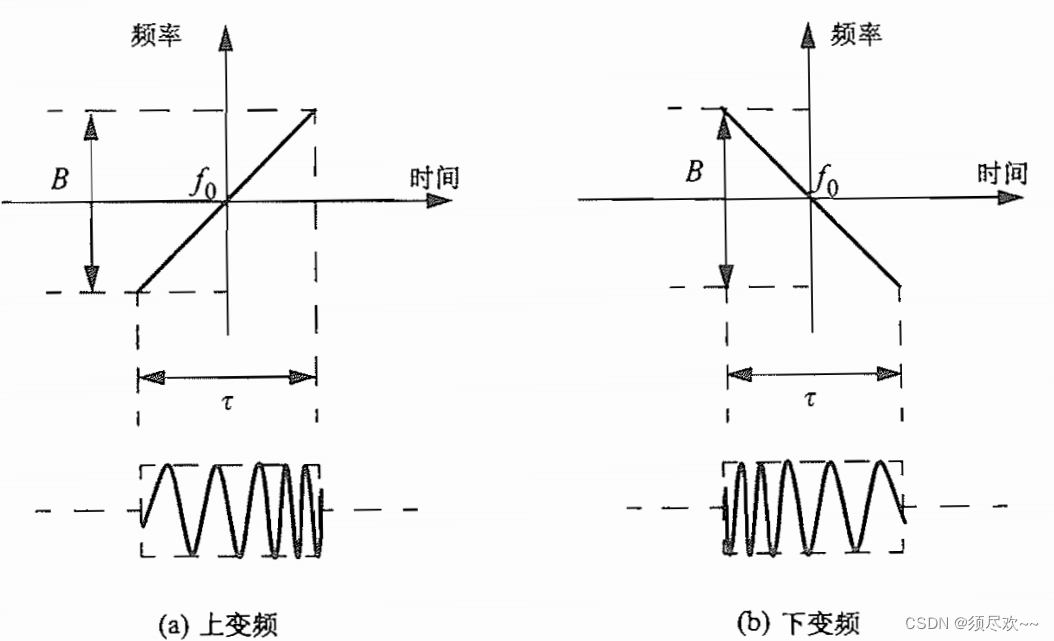
LFM 上变频波形的瞬时相位可以表示为:
ψ
(
t
)
=
2
π
(
f
0
t
+
μ
2
t
2
)
−
τ
2
≤
t
≤
τ
2
\psi(t)=2\pi(f_0t+\frac{\mu}{2}t^2) \qquad -\frac{\tau}{2}\le t\le \frac{\tau}{2}
ψ(t)=2π(f0t+2μt2)−2τ≤t≤2τ
其中,
f
0
f_0
f0 为雷达中心频率,
μ
=
(
2
π
B
)
/
τ
\mu=(2\pi B)/\tau
μ=(2πB)/τ 是 LFM 系数,因此,瞬时频率为
f
(
t
)
=
1
2
π
d
d
t
ψ
(
t
)
=
f
0
+
μ
t
−
τ
2
≤
t
≤
τ
2
f(t)=\frac{1}{2\pi}\frac{d}{dt}\psi(t)=f_0+\mu t \qquad -\frac{\tau}{2}\le t\le \frac{\tau}{2}
f(t)=2π1dtdψ(t)=f0+μt−2τ≤t≤2τ
同理,下变频波形的瞬时相位和频率分别为:
ψ
(
t
)
=
2
π
(
f
0
t
−
μ
2
t
2
)
−
τ
2
≤
t
≤
τ
2
\psi(t)=2\pi(f_0t-\frac{\mu}{2}t^2) \qquad -\frac{\tau}{2}\le t\le \frac{\tau}{2}
ψ(t)=2π(f0t−2μt2)−2τ≤t≤2τ
f ( t ) = 1 2 π d d t ψ ( t ) = f 0 − μ t − τ 2 ≤ t ≤ τ 2 f(t)=\frac{1}{2\pi}\frac{d}{dt}\psi(t)=f_0-\mu t \qquad -\frac{\tau}{2}\le t\le \frac{\tau}{2} f(t)=2π1dtdψ(t)=f0−μt−2τ≤t≤2τ
2、时域表达式
典型的线性调频信号可以表示为:
s
(
t
)
=
r
e
c
t
(
t
τ
)
e
j
2
π
(
f
0
t
+
μ
2
t
2
)
s(t)=rect(\frac{t}{\tau})e^{j2\pi (f_0t+\frac{\mu}{2}t^2)}
s(t)=rect(τt)ej2π(f0t+2μt2)
其中,
r
e
c
t
(
t
/
τ
)
rect(t/\tau)
rect(t/τ) 表示宽度为
τ
\tau
τ 的矩形脉冲,则上式可写成:
s
1
(
t
)
=
e
j
2
π
f
0
t
s
(
t
)
s_1(t)=e^{j2\pi f_0}ts(t)
s1(t)=ej2πf0ts(t)
其中:
s
(
t
)
=
r
e
c
t
(
t
τ
)
e
j
π
μ
t
2
s(t)=rect(\frac{t}{\tau})e^{j\pi \mu t^2}
s(t)=rect(τt)ejπμt2 是
s
1
(
t
)
s_1(t)
s1(t) 的复包络。
3、频域表达式
信号
s
1
(
t
)
s_1(t)
s1(t) 的频谱由它的复包络
s
(
t
)
s(t)
s(t) 决定,
s
1
(
t
)
s_1(t)
s1(t) 中的复指数项表示中心频率
f
0
f_0
f0 的频移。将
s
(
t
)
s(t)
s(t) 进行傅里叶变换,得到
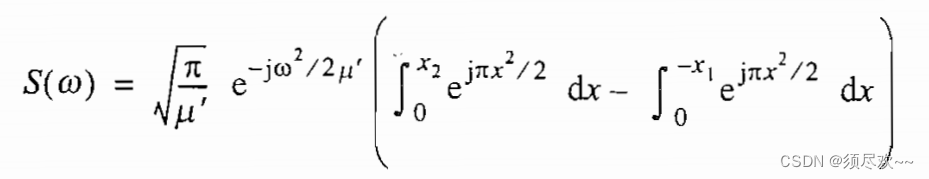
其中:
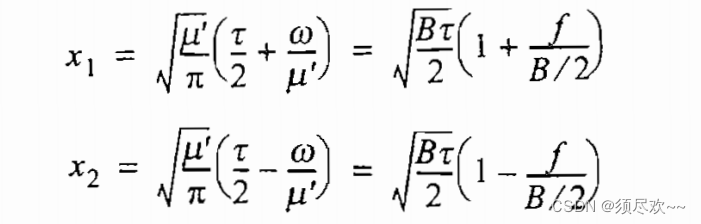
用
C
(
x
)
C(x)
C(x) 和
S
(
x
)
S(x)
S(x) 表示菲涅尔积分,定义如下:
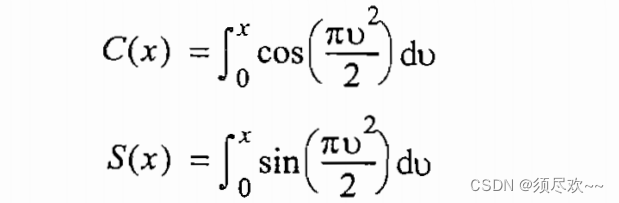
菲涅尔积分近似为:
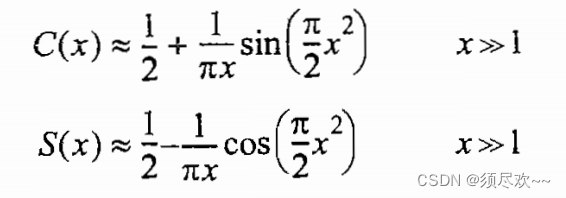
注意:
C
(
−
x
)
=
−
C
(
x
)
,
S
(
−
x
)
=
−
S
(
x
)
C(-x)=-C(x),S(-x)=-S(x)
C(−x)=−C(x),S(−x)=−S(x)
将菲涅尔积分代入 LFM 频域表达式
S
(
ω
)
S(\omega)
S(ω),得到:
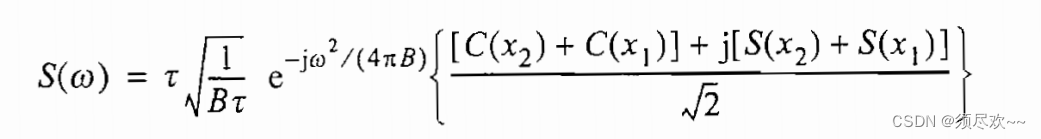
二、MATLAB 仿真
1、涅菲尔积分
①、MATLAB 源码
clear all
close all
n = 0;
for x = 0:.05:4
n = n+1;
sx(n) = quadl('fresnels',.0,x);
cx(n) = quadl('fresnelc',.0,x);
end
plot(cx)
x=0:.05:4;
plot(x,cx,'k',x,sx,'k--')
grid
xlabel ('x')
ylabel ('Fresnel integrals: C(x); S(x)')
legend('C(x)','S(x)')
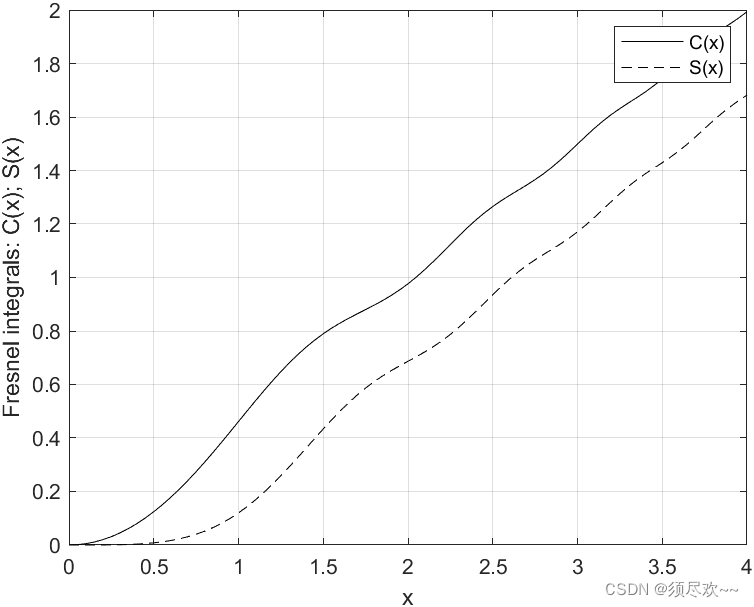
②、仿真结果
下图为
C
(
x
)
C(x)
C(x) 和
S
(
x
)
S(x)
S(x) 在
0
≤
x
≤
4.0
0\le x \le 4.0
0≤x≤4.0时的图形
2、LFM
①、MATLAB 源码
下述为绘制 LFM 信号实部、虚部及幅度谱的典型图形。
close all
clear all
eps = 0.000001;
%Enter pulse width and bandwidth
B = 200.0e6; %200 MHZ bandwidth
T = 10.e-6; %10 micro second pulse;
% Compute alpha
mu = 2. * pi * B / T;
% Determine sampling times
delt = linspace(-T/2., T/2., 10001); % 1 nano sceond sampling interval
% Compute the complex LFM representation
Ichannal = cos(mu .* delt.^2 / 2.); % Real part
Qchannal = sin(mu .* delt.^2 / 2.); % Imaginary Part
LFM = Ichannal + sqrt(-1) .* Qchannal; % complex signal
%Compute the FFT of the LFM waveform
LFMFFT = fftshift(fft(LFM));
% Plot the real and Immaginary parts and the spectrum
freqlimit = 0.5 / 1.e-9;% the sampling interval 1 nano-second
freq = linspace(-freqlimit/1.e6,freqlimit/1.e6,10001);
figure(1)
plot(delt*1e6,Ichannal,'k');
axis([-1 1 -1 1])
grid
xlabel('Time - microsecs')
ylabel('Real part')
title('T = 10 Microsecond, B = 200 MHz')
figure(2)
plot(delt*1e6,Qchannal,'k');
axis([-1 1 -1 1])
grid
xlabel('Time - microsecs')
ylabel('Imaginary part')
title('T = 10 Microsecond, B = 200 MHz')
figure(3)
plot(freq, abs(LFMFFT),'k');
%axis tight
grid
xlabel('Frequency - MHz')
ylabel('Amplitude spectrum')
title('Spectrum for an LFM waveform and T = 10 Microsecond, B = 200 MHZ')
B 的值为 200.0e6,表示 200 MHz 的带宽。T 的值为 10.e-6,表示 10 微秒的脉冲宽度。
②、仿真结果
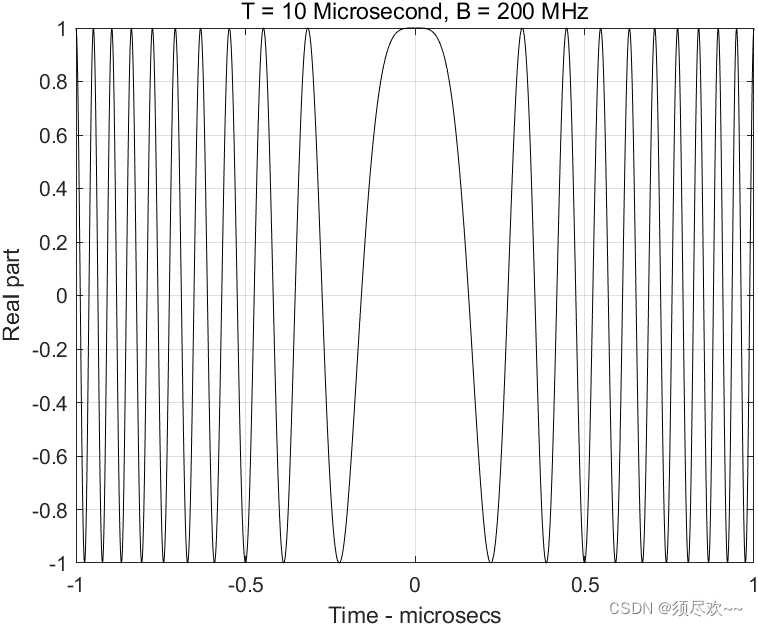
1) 典型 LFM 波形,实部
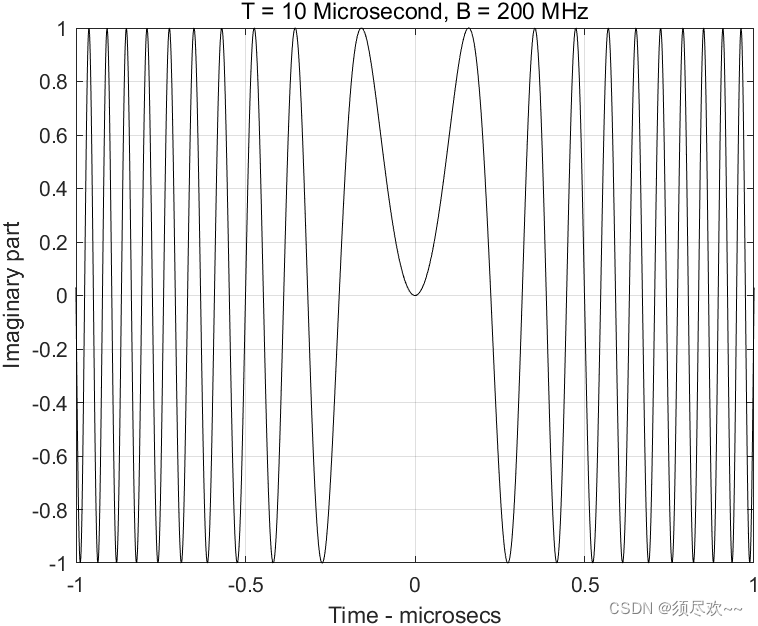
2) 典型 LFM 波形,虚部
3) LFM 波形的典型谱
下图中类似方形的频谱就是广为人知的菲涅尔谱。
我的qq:2442391036,欢迎交流!