文章目录
- 1 哈密尔顿回路
- 2 哈密尔顿回路算法实现
- 2.1 常规回溯算法
- 2.2 引入变量记录剩余未访问的节点数量
- 3 哈密尔顿路径问题
- 4 状态压缩
- 4.1 查看第i位是否为1
- 4.2 设置第i位是为1或者0
- 4.3 小结
- 4.4 状态压缩在哈密尔顿问题中的应用
- 5 记忆化搜索
- 5.1 记忆化搜索与递推区别
- 5.2 记忆化搜索的实现 - 力扣980
1 哈密尔顿回路
求解哈密尔顿回路
如何求解一个图是否存在哈密尔顿回路呢?
一个最直观的想法就是暴力求解。暴力求解的思路也很简单:我们遍历图的每一个顶点 v,然后从顶点 v 出发,看是否能够找到一条哈密尔顿回路。
暴力求解的代价同求解全排列问题是等价的,其时间复杂度为 O ( N ! ) O(N!) O(N!),N 为图的顶点的个数。
那么除了暴力求解哈密尔顿回路问题,是否存在更好的算法?
很遗憾我们只能在暴力破解的基础上,尽量去做到更多的优化,譬如回溯剪枝,记忆化搜索等,但是,还没有找到一种多项式级别的算法来解决哈密尔顿问题。
通常,这类问题也被称为 NP(Non-deterministic Polynomial)难问题。
综上所述,求解哈密尔顿回路,我们可以采用回溯+剪枝的思想来进行求解。
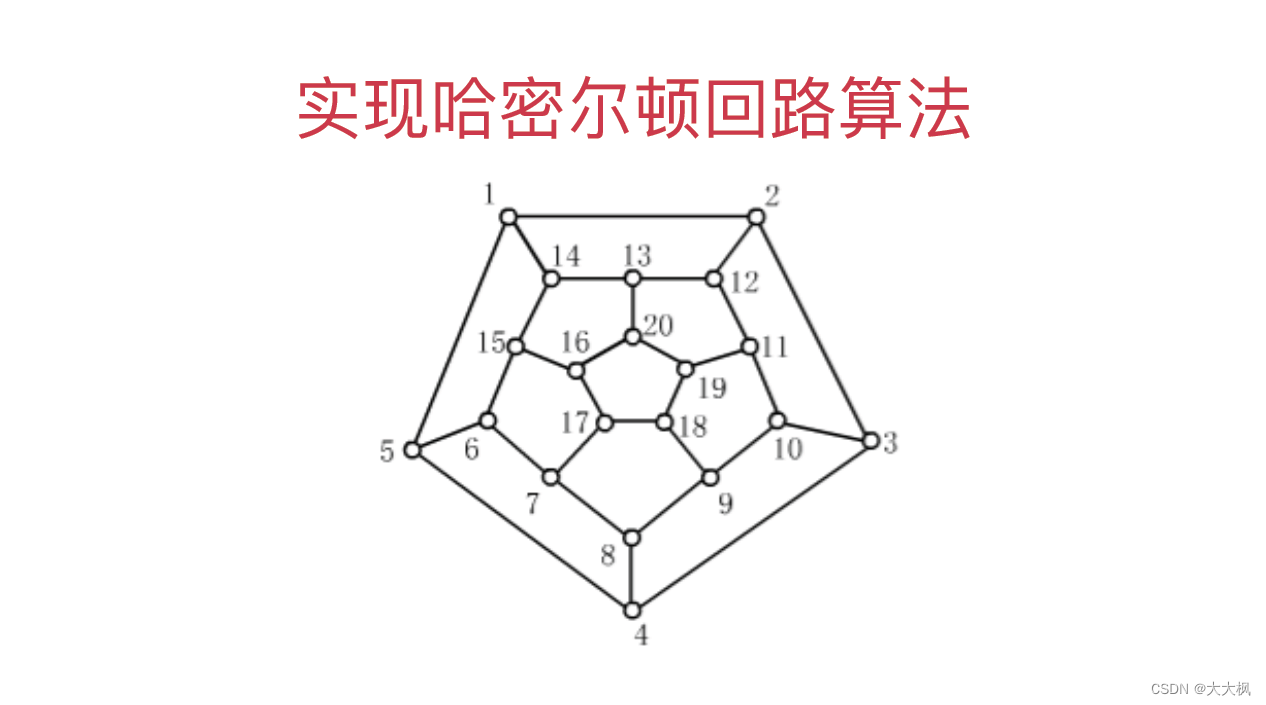
2 哈密尔顿回路算法实现
2.1 常规回溯算法
package Chapter07_Hamilton_Loop_And_Path.Hamilton_Loop;
import java.util.ArrayList;
import java.util.Collections;
public class HamiltonLoop {
private Graph G;
private boolean[] visited;
private int[] pre;
private int end; //用来表示最后一个被遍历的顶点
public HamiltonLoop(Graph G){
this.G = G;
visited = new boolean[G.V()];
pre = new int[G.V()];
end = -1;
dfs(0, 0);
}
private boolean dfs(int v, int parent){
visited[v] = true;
pre[v] = parent;
for(int w: G.adj(v))
if(!visited[w]){
if(dfs(w, v))
return true;
}
else if(w == 0 && allVisited()){ //如果回到起始点0并且所有的点都被访问过了,则找到了哈密尔回路
end = v;
return true;
}
// 回溯
visited[v] = false;
return false;
}
public ArrayList<Integer> result(){
ArrayList<Integer> res = new ArrayList<>();
if(end == -1) return res;
int cur = end;
while(cur != 0){
res.add(cur);
cur = pre[cur];//上一个节点
}
res.add(0);
Collections.reverse(res);
return res;
}
private boolean allVisited(){
for(int v = 0; v < G.V(); v ++)
if(!visited[v]) return false;
return true;
}
public static void main(String[] args){
Graph g = new Graph("g9.txt");
HamiltonLoop hl = new HamiltonLoop(g);
System.out.println(hl.result());
Graph g2 = new Graph("g10.txt");
HamiltonLoop hl2 = new HamiltonLoop(g2);
System.out.println(hl2.result());
}
}
2.2 引入变量记录剩余未访问的节点数量
package Chapter07_Hamilton_Loop_And_Path.Hamilton_Loop;
import java.util.ArrayList;
import java.util.Collections;
public class HamiltonLoop_Optimization {
private Graph G;
private boolean[] visited;
private int[] pre;
private int end;
public HamiltonLoop_Optimization(Graph G){
this.G = G;
visited = new boolean[G.V()];
pre = new int[G.V()];
end = -1;
//dfs的过程记录剩余未访问的节点的数量
dfs(0, 0, G.V());
}
private boolean dfs(int v, int parent, int left){
visited[v] = true;
pre[v] = parent;
left --;
//出口:如果未访问的节点是0,并且当前节点和初始节点有边
if(left == 0 && G.hasEdge(v, 0)){
end = v;
return true;
}
for(int w: G.adj(v))
if(!visited[w]){
if(dfs(w, v, left)) return true;
}
// else if(w == 0 && left == 0){
// end = v;
// return true;
// }
visited[v] = false;
return false;
}
public ArrayList<Integer> result(){
ArrayList<Integer> res = new ArrayList<>();
if(end == -1) return res;
int cur = end;
while(cur != 0){
res.add(cur);
cur = pre[cur];
}
res.add(0);
Collections.reverse(res);
return res;
}
public static void main(String[] args){
Graph g = new Graph("g9.txt");
HamiltonLoop hl = new HamiltonLoop(g);
System.out.println(hl.result());
Graph g2 = new Graph("g10.txt");
HamiltonLoop hl2 = new HamiltonLoop(g2);
System.out.println(hl2.result());
}
}
3 哈密尔顿路径问题
根据出发位置的不同,路径也会不一样。但是算法实现还是一致的,只需要修改构造函数,传入起点位置。
package Chapter07_Hamilton_Loop_And_Path.Hamilton_Loop;
import java.util.ArrayList;
import java.util.Collections;
public class HamiltonPath {
private Graph G;
private int s;
private boolean[] visited;
private int[] pre;
private int end;
public HamiltonPath(Graph G, int s){
this.G = G;
this.s = s;
visited = new boolean[G.V()];
pre = new int[G.V()];
end = -1;
dfs(s, s, G.V());
}
private boolean dfs(int v, int parent, int left){
visited[v] = true;
pre[v] = parent;
left --;
if(left == 0){
end = v;
return true;
}
for(int w: G.adj(v))
if(!visited[w]){
if(dfs(w, v, left)) return true;
}
visited[v] = false;
return false;
}
public ArrayList<Integer> result(){
ArrayList<Integer> res = new ArrayList<>();
if(end == -1) return res;
int cur = end;
while(cur != s){
res.add(cur);
cur = pre[cur];
}
res.add(s);
Collections.reverse(res);
return res;
}
public static void main(String[] args){
Graph g = new Graph("g10.txt");
HamiltonPath hp = new HamiltonPath(g, 0);
System.out.println(hp.result());
HamiltonPath hp2 = new HamiltonPath(g, 1);
System.out.println(hp2.result());
}
}
4 状态压缩

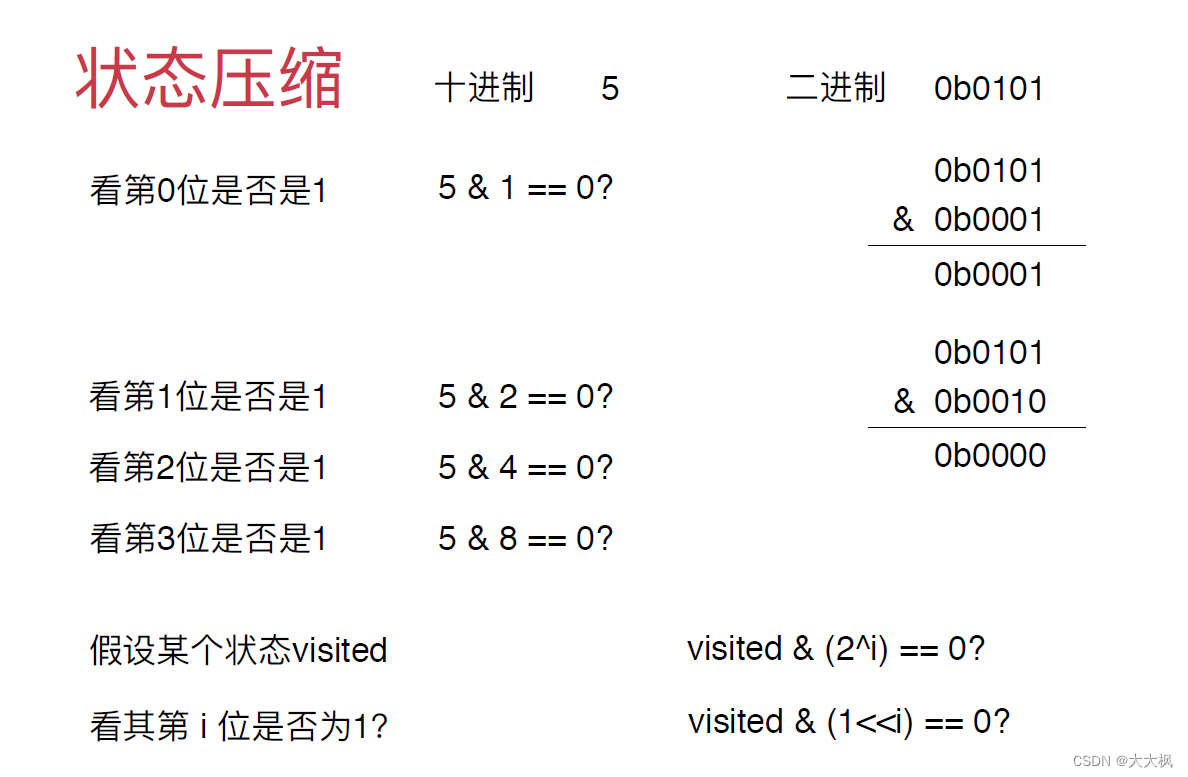
4.1 查看第i位是否为1
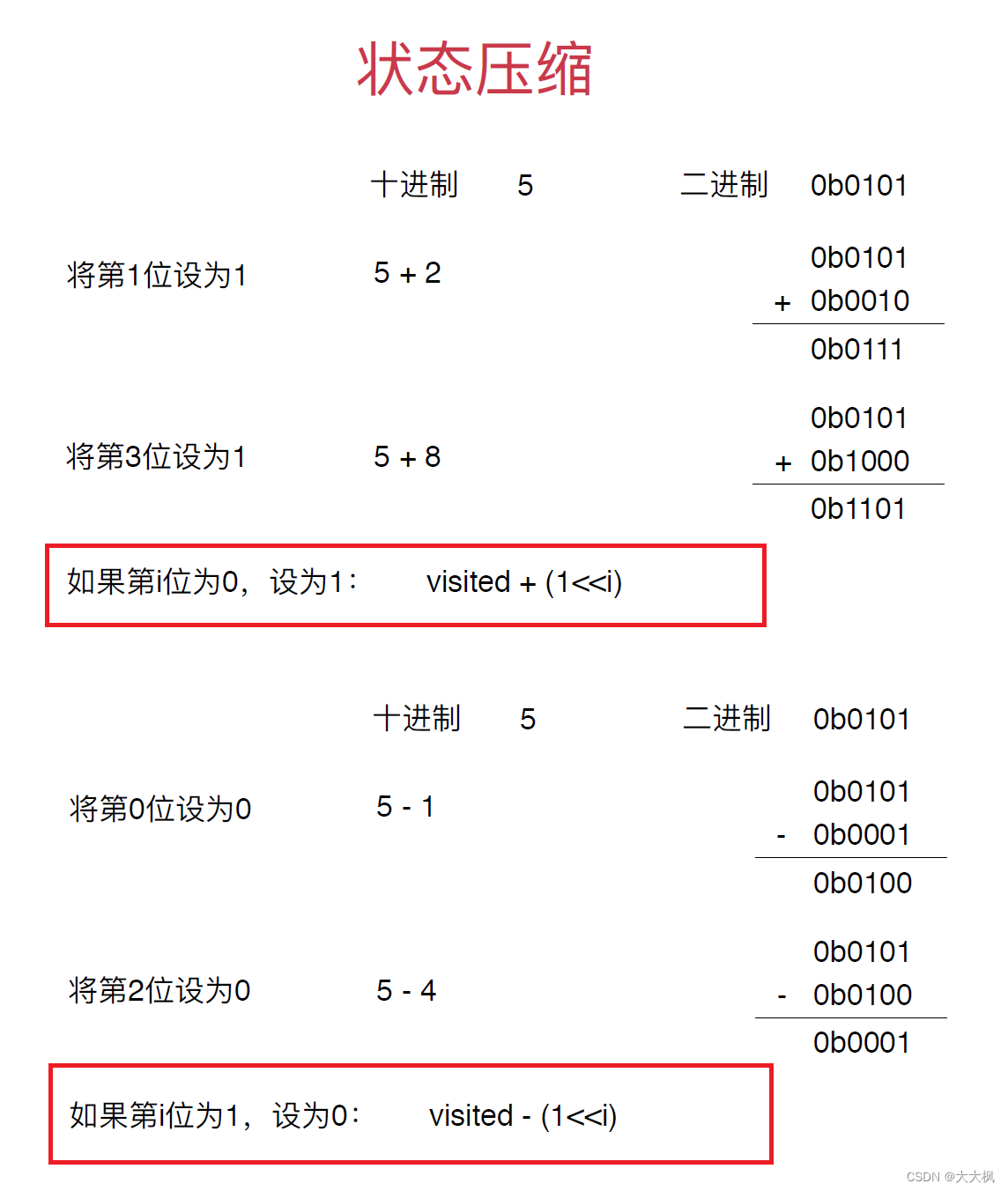
4.2 设置第i位是为1或者0
4.3 小结

4.4 状态压缩在哈密尔顿问题中的应用
在我们的代码中,一直都使用布尔型的 visited 数组来记录图中的每一个顶点是否有被遍历过。
在算法面试中,对于像哈密尔顿回路/路径这样的 NP 难问题,通常都会有输入限制,一般情况下,求解问题中给定的图不会超过 30 个顶点。
这样,在算法笔试/面试中,我们就可以对 visited 数组进行状态压缩来优化算法类执行的效率。我们知道一个 int 型的数字有 32 位,每一位不是 1 就是 0,这正好对应了布尔型的 true 和 false。
所以,我们可以将 visited 数组简化成一个数字,该数字的每一个比特位用来表示 visited 数组的每一个 true 或 false 值。
来看一下我们的 HamiltonLoop 中 dfs 的代码:
public HamiltonLoop_StateCompression(Graph G){
this.G = G;
pre = new int[G.V()];
end = -1;
int visited = 0; //用一个数的比特位来表示是否被访问过
dfs(visited, 0, 0, G.V());
}
private boolean dfs(int visited, int v, int parent, int left){
visited += (1 << v); //第v位置设置为1
pre[v] = parent;
left --;
if(left == 0 && G.hasEdge(v, 0)){
end = v;
return true;
}
for(int w: G.adj(v))
if((visited & (1 << w)) == 0){ //看数字的第w个位置是否为 0
if(dfs(visited, w, v, left)) return true;
}
visited -= (1 << v); //回溯,第v位置恢复为0
return false;
}
5 记忆化搜索
记忆化搜索是动态规划的一种实现方式。
在记忆化搜索中,当算法需要计算某个子问题的结果时,它首先检查是否已经计算过该问题。如果已经计算过,则直接返回已经存储的结果;否则,计算该问题,并将结果存储下来以备将来使用。
举个例子,比如「斐波那契数列」的定义是: f ( 0 ) = 0 , f ( 1 ) = 1 , f ( n ) = f ( n − 1 ) + f ( n − 2 ) f(0) = 0, f(1) = 1, f(n) = f(n - 1) + f(n - 2) f(0)=0,f(1)=1,f(n)=f(n−1)+f(n−2)。如果我们使用递归算法求解第 n n n 个斐波那契数,则对应的递推过程如下:
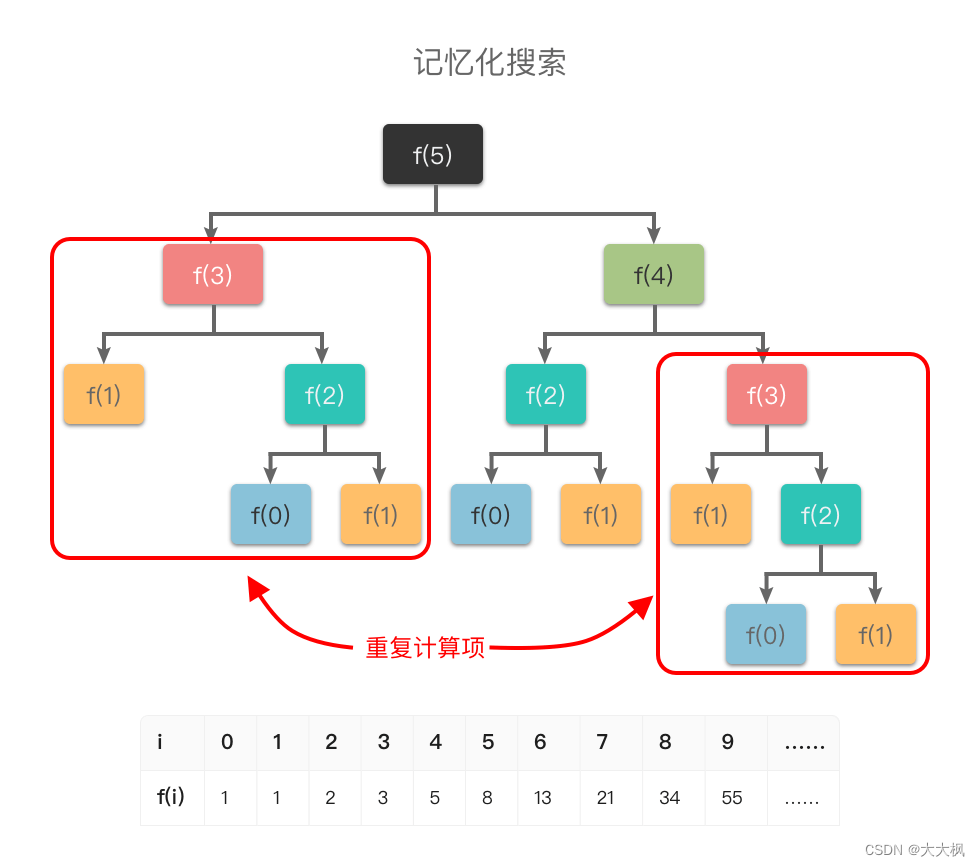
从图中可以看出:如果使用普通递归算法,想要计算
f
(
5
)
f(5)
f(5),需要先计算
f
(
3
)
f(3)
f(3) 和
f
(
4
)
f(4)
f(4),而在计算
f
(
4
)
f(4)
f(4) 时还需要计算
f
(
3
)
f(3)
f(3)。这样
f
(
3
)
f(3)
f(3) 就进行了多次计算,同理
f
(
0
)
f(0)
f(0)、
f
(
1
)
f(1)
f(1)、
f
(
2
)
f(2)
f(2) 都进行了多次计算,从而导致了重复计算问题。
为了避免重复计算,在递归的同时,我们可以使用一个缓存(数组或哈希表)来保存已经求解过的 f ( k ) f(k) f(k) 的结果。如上图所示,当递归调用用到 f ( k ) f(k) f(k) 时,先查看一下之前是否已经计算过结果,如果已经计算过,则直接从缓存中取值返回,而不用再递推下去,这样就避免了重复计算问题。
5.1 记忆化搜索与递推区别
记忆化搜索:「自顶向下」的解决问题,采用自然的递归方式编写过程,在过程中会保存每个子问题的解(通常保存在一个数组或哈希表中)来避免重复计算。
优点:代码清晰易懂,可以有效的处理一些复杂的状态转移方程。有些状态转移方程是非常复杂的,使用记忆化搜索可以将复杂的状态转移方程拆分成多个子问题,通过递归调用来解决。
缺点:可能会因为递归深度过大而导致栈溢出问题。
递推:「自底向上」的解决问题,采用循环的方式编写过程,在过程中通过保存每个子问题的解(通常保存在一个数组或哈希表中)来避免重复计算。
优点:避免了深度过大问题,不存在栈溢出问题。计算顺序比较明确,易于实现。
缺点:无法处理一些复杂的状态转移方程。有些状态转移方程非常复杂,如果使用递推方法来计算,就会导致代码实现变得非常困难。
- 记忆化搜索解题步骤
我们在使用记忆化搜索解决问题的时候,其基本步骤如下:
- 写出问题的动态规划「状态」和「状态转移方程」。 定义一个缓存(数组或哈希表),用于保存子问题的解。
- 定义一个递归函数,用于解决问题。在递归函数中,首先检查缓存中是否已经存在需要计算的结果,如果存在则直接返回结果,否则进行计算,并将结果存储到缓存中,再返回结果。
- 在主函数中,调用递归函数并返回结果。
5.2 记忆化搜索的实现 - 力扣980
package Chapter07_HamiltonLoop_And_StateCompression_And_MemoizationSearch.Memoization_Search;
import java.util.Arrays;
// Leetcode 980
class Solution {
private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
private int R, C;
private int[][] grid;
private int start, end;
private int[][] memo;
public int uniquePathsIII(int[][] grid) {
this.grid = grid;
R = grid.length;
C = grid[0].length;
int left = R * C;
memo = new int[1 << (R * C)][R * C];
for(int i = 0; i < memo.length; i ++)
Arrays.fill(memo[i], -1);
for(int i = 0; i < R; i ++)
for(int j = 0; j < C; j ++)
if(grid[i][j] == 1){
start = i * C + j;
grid[i][j] = 0;
}
else if(grid[i][j] == 2){
end = i * C + j;
grid[i][j] = 0;
}
else if(grid[i][j] == -1)
left --;
int visited = 0;
return dfs(visited, start, left);
}
private int dfs(int visited, int v, int left){
if(memo[visited][v] != -1) return memo[visited][v];
visited += (1 << v);
left --;
if(v == end && left == 0){
visited -= (1 << v);
memo[visited][v] = 1;
return 1;
}
int x = v / C, y = v % C;
int res = 0;
for(int d = 0; d < 4; d ++){
int nextx = x + dirs[d][0], nexty = y + dirs[d][1];
int next = nextx * C + nexty;
if(inArea(nextx, nexty) && grid[nextx][nexty] == 0 && (visited & (1 << next)) == 0)
res += dfs(visited, next, left);
}
visited -= (1 << v);
memo[visited][v] = res;
return res;
}
private boolean inArea(int x, int y){
return x >= 0 && x < R && y >= 0 && y < C;
}
}