674. 最长连续递增序列

题目：

给定一个未经排序的整数数组nums，找到最长且 连续递增的子序列，并返回该序列的长度。

dp数组含义：

dp[i]：以下标i为结尾的连续递增的子序列长度为dp[i]。

递推公式：

怎么推出来dp[i]呢，从左到右遍历数组的时候，如果后一个比前一个大，则代表连续而且递增的关系，又因为求的长度，所以没符合一次就在后一位的dp基础上+1

抽象为

if（nums[i]>nums[i-1]）dp[i]=dp[i-1]+1

for (int i = 1; i < nums.size(); i++) {
    if (nums[i] > nums[i - 1]) { // 连续记录
        dp[i] = dp[i - 1] + 1;
    }
}

 总代码

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        int result = 1;
        vector<int> dp(nums.size() ,1);//初始化
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i] > nums[i - 1]) { // 连续记录
                dp[i] = dp[i - 1] + 1;
            }
            if (dp[i] > result) result = dp[i];
        }
        return result;
    }
};

 718. 最长重复子数组 

题目：

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。要求连续。

思路：

没思路根据打印图倒推，先看看dp数组含义

dp数组含义：

dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。 （特别注意： “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 ）

然后看图：

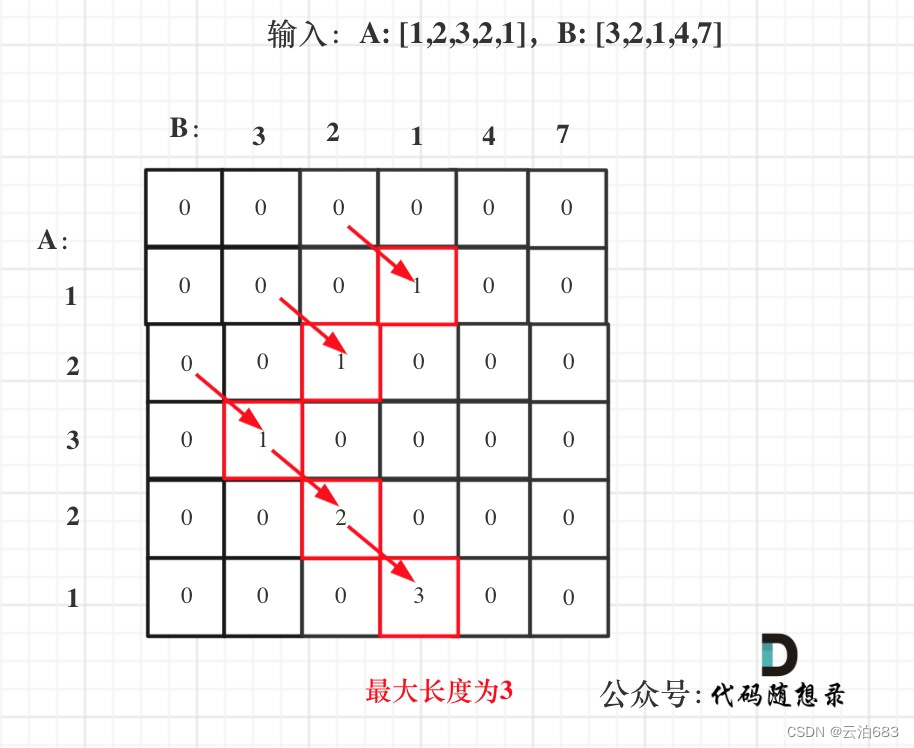
 看见图里，但两个数组遇见相同的值了，就长度就+1，其他的都是0，可以看出dp[i][j]的状态继承dp[i-1][j-1]而来

然后看递推公式：

        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }

 这里的条件，如果nums1的 i 和nums2的 j 在遍历的时候，nums1[i-1]和nums2[j-1]的值相等了，后续dp就+1，相当于连续而且上一步相等就+1的意思，我尝试了下A加了9，1，B加0，1来推导

发现0 0 0 0 0 0 0 0

       0 0 0 1 0 0 0 0  

这里的dp[i][j]，也是继承dp[i-1][j-1]但是数组推导的结果变成了1，大概意思就是这段代码记录下了每一个连续的公共子序列长度。然后把记录下的最长的长度拿出来返回即可。

（全初始化为0，方便遇见单个相同的子序列变成1）

总代码：

（过程理解了，但思路怎么来的不懂）

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};

1143.最长公共子序列

题目：

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

思路：

dp数组含义：

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

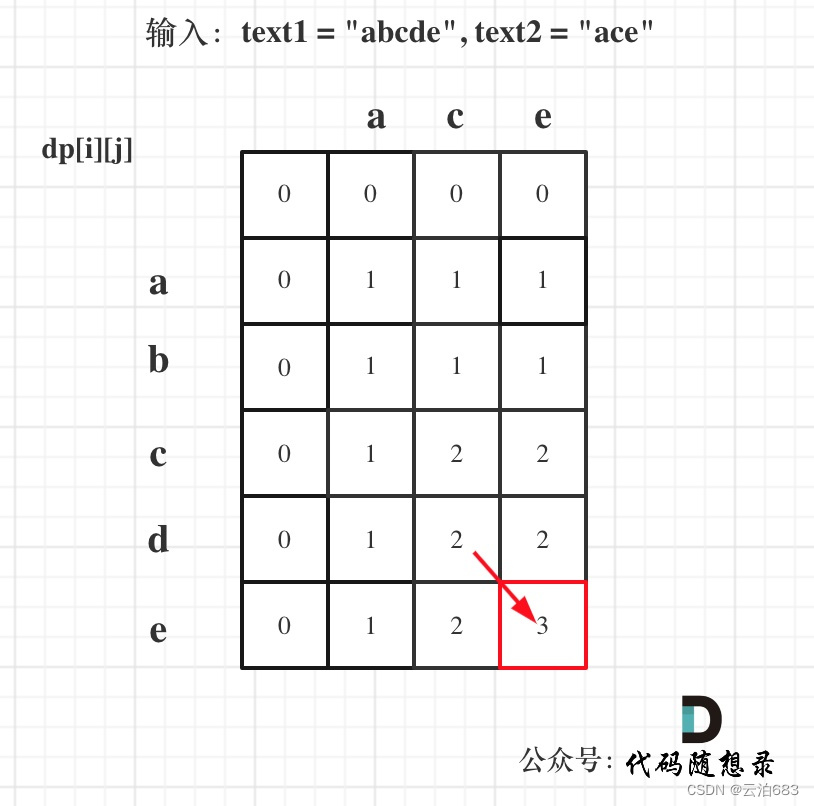
                if (text1[i - 1] == text2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;//找到一个相同的
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);//没找到
                }

 依照遍历的哪一格上面 左面的的值，相等dp值+1，不相等去两面中最大的那个dp值。

总代码

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
        for (int i = 1; i <= text1.size(); i++) {
            for (int j = 1; j <= text2.size(); j++) {
                if (text1[i - 1] == text2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

1035.不相交的线 

 题目：给两个两个并排的数组，把两数组里相同的数字用直线相连，求最大的相连数，不能同数组相连。

思路：

相当于求718最长公共子序列这道题，不改变原始顺序的最长公共子序列（不求连续）内，相同数字直接相连

 不会交叉，至于为啥，下面如果124是公共子序列，那么，原始顺序中44 22 就交叉了，而按照第一段的说法就不会，代码一样的，力扣运行改下字符串名字

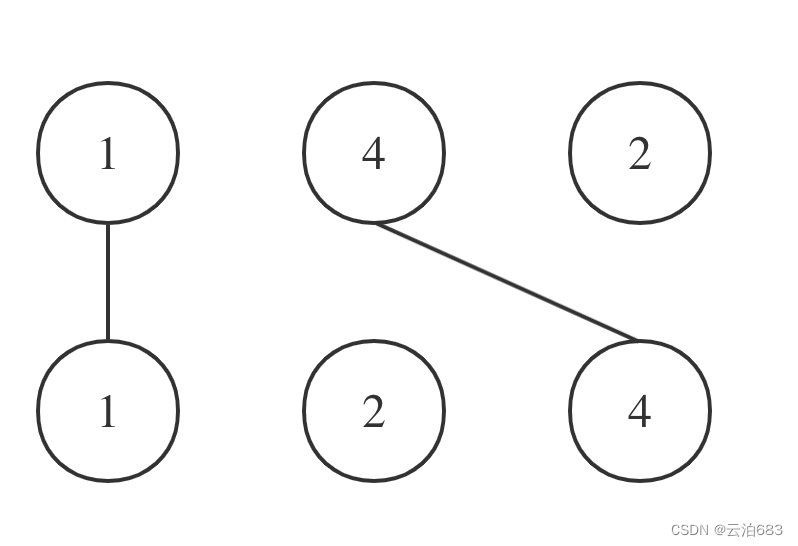
总代码： 

class Solution {
public:
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
        vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));
        for (int i = 1; i <= A.size(); i++) {
            for (int j = 1; j <= B.size(); j++) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[A.size()][B.size()];
    }
};

 总结：所以这些思路是怎么推出来的，，我都是倒退代码看遍历过程的。