一、递归的概念
引例:
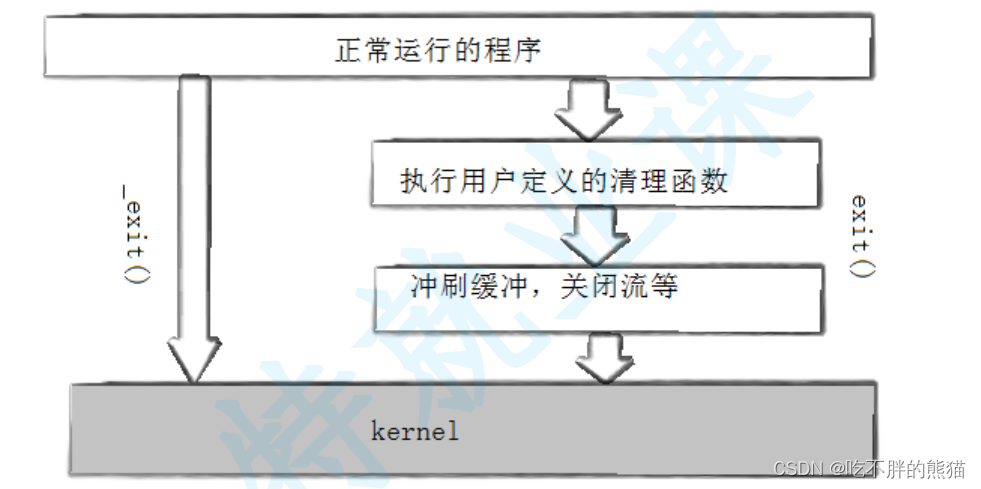
 一个方法在执行过程中调用自身,就称为递归(函数自己调用自己)
一个方法在执行过程中调用自身,就称为递归(函数自己调用自己)
递归相当于数学的数学归纳法,有一个起始条件,有一个递推公式
递归的必要条件
1.将原问题划分为子问题,注意:子问题必须要与原问题解法相同。
2.递归出口(自己调用自己,且有一个结束条件) 分为递、归两个问题

如果遇到栈溢出的问题就是结束条件不对

引例
public static void fun(int a){
if(a==1){
return;
}
System.out.println(a);
fun(a-1);
}
public static void main0(String[] args) {
fun(3);
}运行结果
二、递归联系习题
1.递归求N的阶乘
思路
传入n的值,当n=1时候,阶乘为1,当n不为1的时候,递归调用方法乘以n-1;
代码实现
//1.递归求 N 的阶乘
public static int Fac(int n){
if(n==1){
return 1;
}else{
int t=n*Fac(n-1);
return t;
}
}
public static void main(String[] args) {
int n=0;
System.out.println("请您输入想要求阶乘的数字");
Scanner sc=new Scanner(System.in);
n=sc.nextInt();
int sum=Fac(n);
System.out.println("递归的结果阶乘为"+sum);
}运行结果
2.输入一个整数,求每位组成数字之和,递归实现
思路
输入一个整数,传递参数,首先递归计算到最前的一位,并将其保留,然后进行归并打印
递的过程:准备工作
归的过程:整理与完善工作

代码实现
//2.输入一个整数,求每位组成数字之和,递归实现
public static void print(int n)
{
//结束条件
if(n<10){
System.out.print(n);
System.out.print(" ");
return;
}else {
//递归条件
print(n / 10);
System.out.print(n % 10);
System.out.print(" ");
}
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
System.out.println("请您输入一个整数");
int n=sc.nextInt();
print(n);
}
运行结果
3.递归返回组成数字之和
思路
对传递的数字进行取余和除以10的操作,传递给一个求值总数的数字,将求值的数字传递回来,得出结果
代码实现
public static int num(int n){
if(n<10){
return n;
}
int tmp=n%10+num(n/10);
return tmp;
}
public static void main(String[] args) {
System.out.println("请您输入你想要计算的数字");
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int sum=num(n);
System.out.println(sum);
}运行结果
4.求斐波那契数列的前n项
4.1递归实现
思路
传入参数,当参数为1/2时,斐波那契数列传递为1,当参数大于2时,斐波那契数列返回前一项和前两项的数字之和,最终得出第n项斐波那契数列的值
代码实现
//4.递归求斐波那契数列的第 N 项
public static int Fib(int n){
if(n==1||n==2){
return 1;
}else{
return Fib(n-1)+Fib(n-2);
}
}
public static void main(String[] args) {
System.out.println("请您输入你想要计算的数字");
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
System.out.println(Fib(n));
System.out.println(Fib(5));
}
运行结果

能不使用递归的方式,最后用循环的方式实现斐波那契数列问题,避免出现冗余运算
4.2 循环实现
代码实现
//5.循环求解斐波那契数列问题,求斐波那契数列的第 N 项
public static int fib(int n){
int last1=1;
int last2=1;
int cur=0;
for(int i=3;i<=n;i++){
cur = last1+last2;
last2=last1;
last1=cur;
}
return cur;
}
public static void main(String[] args) {
System.out.println("请您输入你想要计算的数字");
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int cur=fib(n);
System.out.println(cur);
}运行结果

5.汉诺塔问题

* 传入n个盘子,编号从1..n,我就能按照汉诺塔的规则,从目标盘子A -> C ,B是辅助盘
A 起始柱子
B 辅助柱子
C 目标柱子
代码实现
//5.递归求解汉诺塔问题
/*
@param n
@param pos1 起始位置
@param pos2 中转位置
@param pos3 目标位置
*/
public static void hanoi(int n,char pos1,char pos2,char pos3){
if(n==1){
move(pos1,pos3);
return;
}
hanoi(n-1,pos1,pos3,pos2);
move(pos1,pos3);
hanoi(n-1,pos2,pos1,pos3);
}
public static void move(char pos1,char pos2){
System.out.print(pos1+"->"+pos2+" ");
}
public static void main(String[] args) {
System.out.println("请输入你想求解的数字");
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
hanoi(n,'A','B','C');
}运行结果