题目:
2258. 逃离火灾
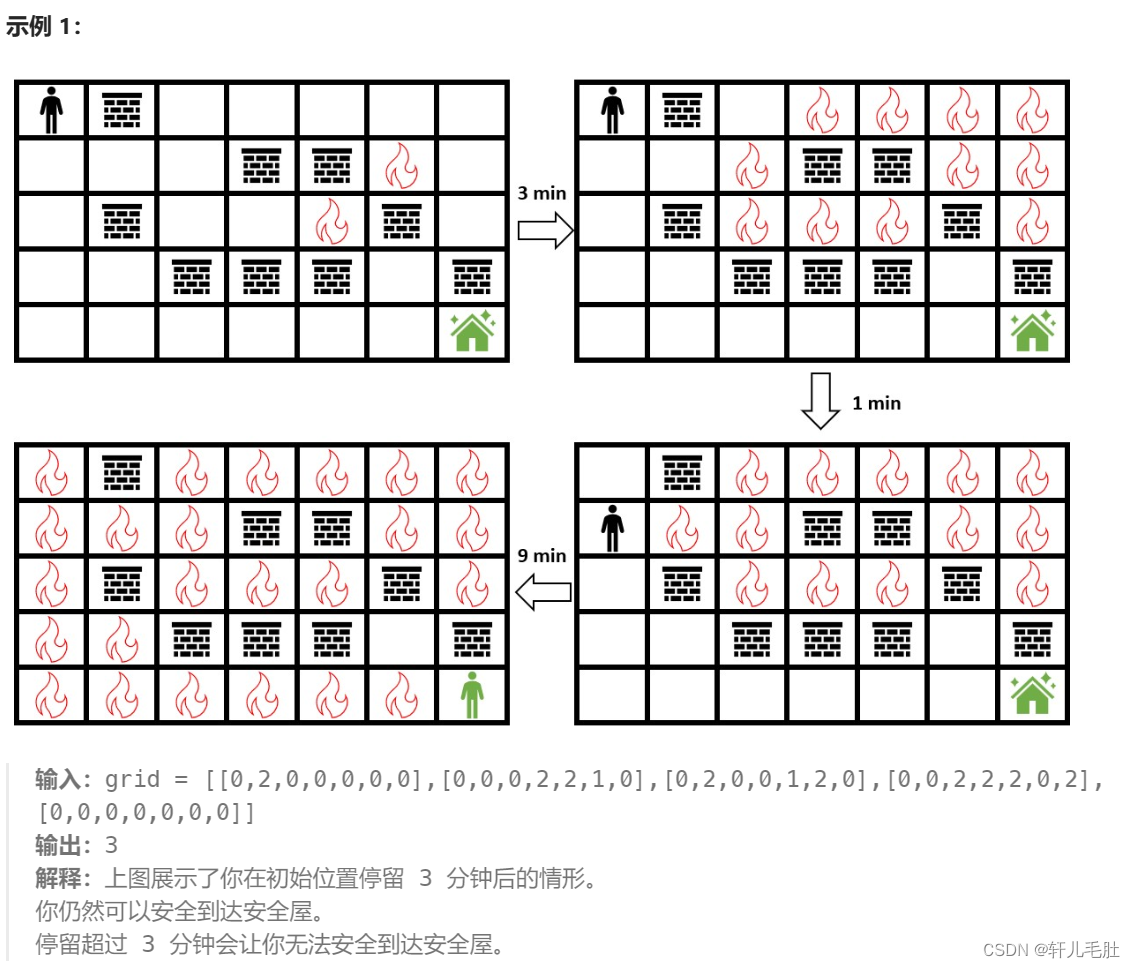
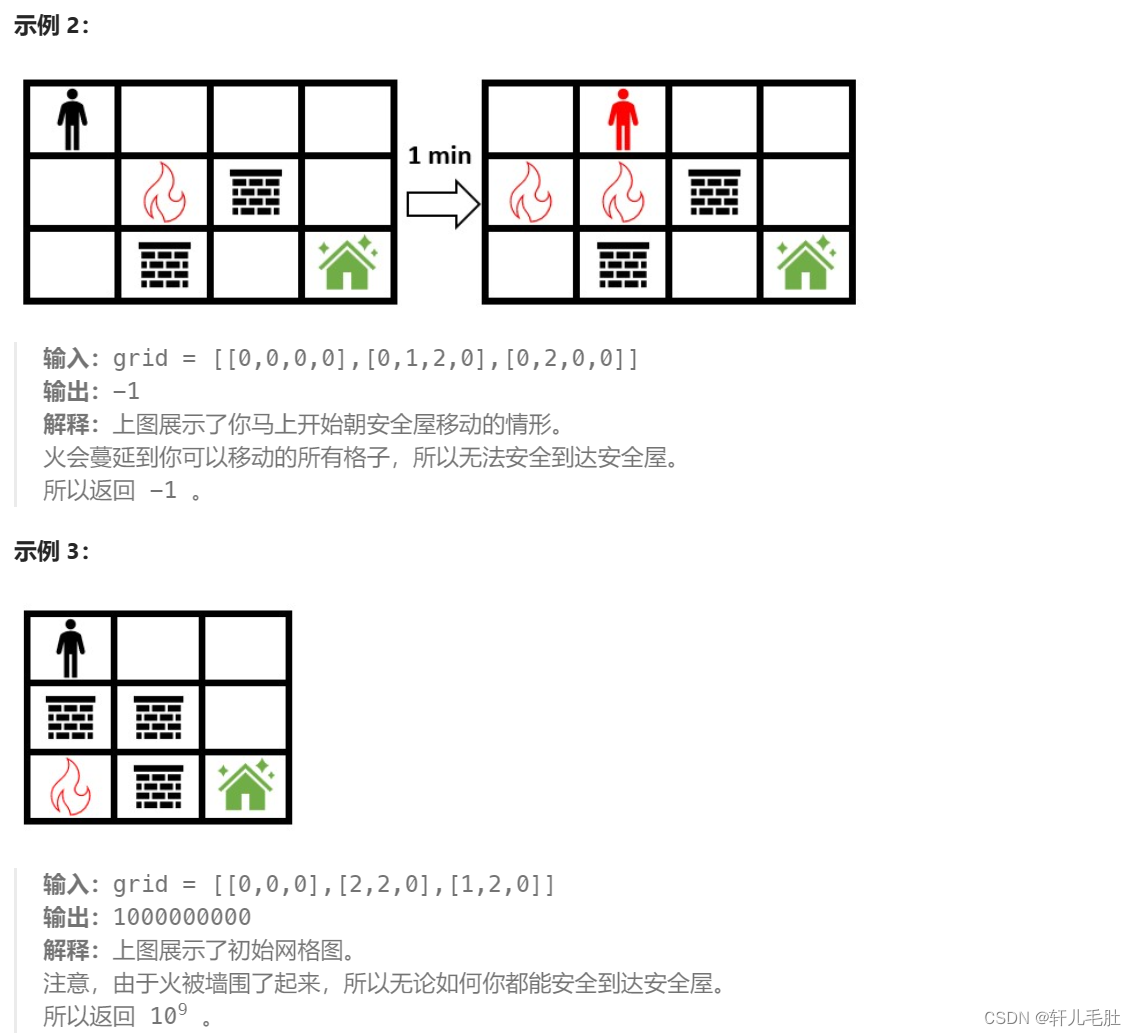
给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ,它表示一个网格图。每个格子为下面 3 个值之一:
0表示草地。1表示着火的格子。2表示一座墙,你跟火都不能通过这个格子。
一开始你在最左上角的格子 (0, 0) ,你想要到达最右下角的安全屋格子 (m - 1, n - 1) 。每一分钟,你可以移动到 相邻 的草地格子。每次你移动 之后 ,着火的格子会扩散到所有不是墙的 相邻 格子。
请你返回你在初始位置可以停留的 最多 分钟数,且停留完这段时间后你还能安全到达安全屋。如果无法实现,请你返回 -1 。如果不管你在初始位置停留多久,你 总是 能到达安全屋,请你返回 109 。
注意,如果你到达安全屋后,火马上到了安全屋,这视为你能够安全到达安全屋。
如果两个格子有共同边,那么它们为 相邻 格子。

解答:
二分 + BFS
火势蔓延是一个固定的过程,只有人员移动需要决策。
假设人员最晚在 t秒后出发,仍能到达安全屋,说明人员对逃走路线的访问,要比火势更快。那么人员在更早的时间点([0,t−1]秒后)出发,必然仍能按照原定路线到达安全屋(火势对路径的影响不变)。
因此,在以 ttt 为分割点的(正整数)数轴上,具有二段性,可运用「二分」求分割点。
假设存在某个判定函数 check,用于检查人员在 xxx 秒后出发能否到达安全屋,那么可知:
当实际延迟出发的秒数,小于等于 t秒,必然能安全到达
当实际延迟出发的描述,超过 t秒,必然不能安全到达
在人员移动路线中,“回头路”是没有意义的,因此人员对每个点的访问次数最多为一次。同时,不考虑墙的阻拦,火势也最多在不超过棋盘大小的时间内完全蔓延。
这指导我们最大延迟出发时间不会超过n×m,可在 [0,n×m]值域内进行二分。
接下来,考虑如何实现 check 函数,函数入参为延迟出发秒数 t,返回值为延迟出发后能否到达安全屋。
首先,对于普通位置,如果火势和人员同时到达,是不允许的,而安全屋 (n−1,m−1)位置的同时到达,是允许的。
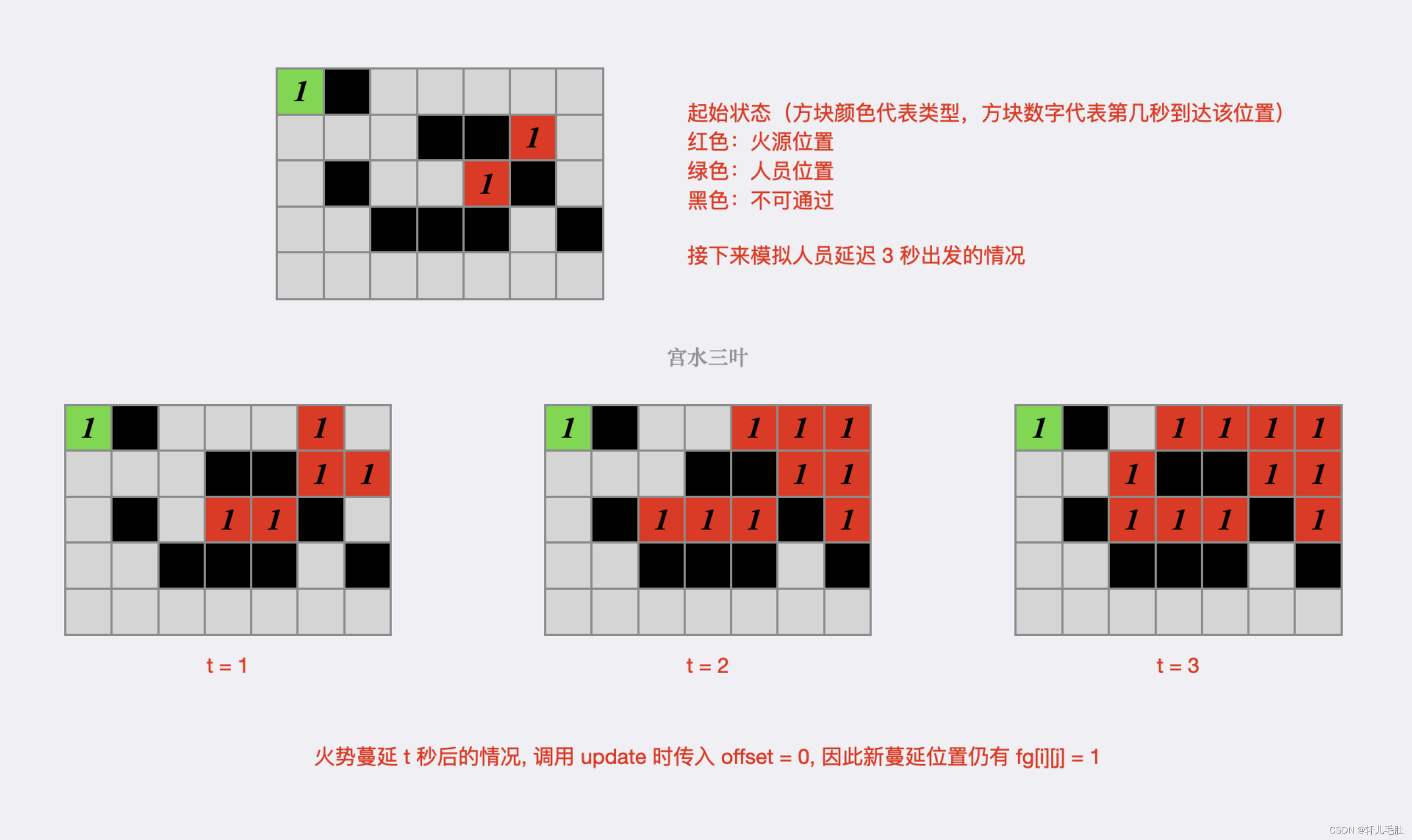
因此,我们需要使用两个二维数组 fg 和 pg 分别记录「火势」和「人员」到达某个位置的最早时间。
创建用于模拟火势蔓延的队列 fire,遍历网格,将火源位置进行入队,更新火源位置 fg[i][j]=1,表示火势在第一秒时最早出现在此处;
运用 BFS,模拟 t秒的火势蔓延,火势在这 ttt 秒内所蔓延到的新位置,均看作为起始火源,即有 fg[i][j]=1。
若执行完 t秒后,火势已蔓延到人员起始位置 (0,0),那么延迟 t秒出发不可行,直接返回 False;
创建用于模拟人员移动的队列 people,将起始位置 (0,0)进行入队,更新 pg[0][0]=1。
运用 BFS,按照「先火后人」的方式,同步模拟「火势蔓延」和「人员移动」过程。普通位置,只要火势蔓延到,那么人将无法移动到此处;安全屋位置,需要判断是否与火势同一时刻到达。
为了方便,将「火势蔓延」和「人员移动」统一成 update 操作,入参包括当前队列 d,标识位 isFire,以及移动偏移量 offset。
在进行t秒的火势蔓延时,调用 t次的 update(fire, true, 0)。在火势和人员同步模拟时,分别调用 update(fire, true, 1) 和 update(people, false, 1)。

代码:
class Solution {
int[][] dirs=new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
int n,m;
boolean ok;
int[][] g,fg,pg;
public int maximumMinutes(int[][] grid) {
g=grid;
n=g.length;
m=g[0].length;
fg=new int[n][m];
pg=new int[n][m];
if(!check(0)) return -1;
int l=0,r=n*m;
while(l<r){
int mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
return r==m*n?(int)1e9:r;
}
boolean check(int t){
ok=false;
Deque<int[]> frie=new ArrayDeque<>();
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
fg[i][j]=pg[i][j]=0;
if(g[i][j]==1){
fg[i][j]=1;
frie.addLast(new int[]{i,j});
}
}
}
while(t-->0) upadte(frie,true,0);//先执行t秒的火势蔓延
if(fg[0][0]!=0) return false;
Deque<int[]> people=new ArrayDeque<>();
pg[0][0]=1;
people.addLast(new int[]{0,0});
while(!people.isEmpty()){
//先火后人,同步进行
upadte(frie,true,1);
upadte(people,false,1);
if(ok) return true;
}
return false;
}
void upadte(Deque<int[]> deque,boolean isFire,int offset){
int sz=deque.size();
while(sz-->0){
int[] info=deque.pollFirst();
int x=info[0],y=info[1];
for(int[] dir:dirs){
int nx=x+dir[0],ny=y+dir[1];
if(nx<0||nx>=n||ny<0||ny>=m) continue;
if(g[nx][ny]==2) continue;
if(isFire){
if(fg[nx][ny]!=0) continue;
fg[nx][ny]=fg[x][y]+offset;
}else{
if(nx==n-1&&ny==m-1&&(fg[nx][ny]==0||fg[nx][ny]==pg[x][y]+offset))
ok=true;//火尚未达到或同时到达
if(fg[nx][ny]!=0||pg[nx][ny]!=0) continue;
pg[nx][ny]=pg[x][y]+offset;
}
deque.addLast(new int[]{nx,ny});
}
}
}
}结果: