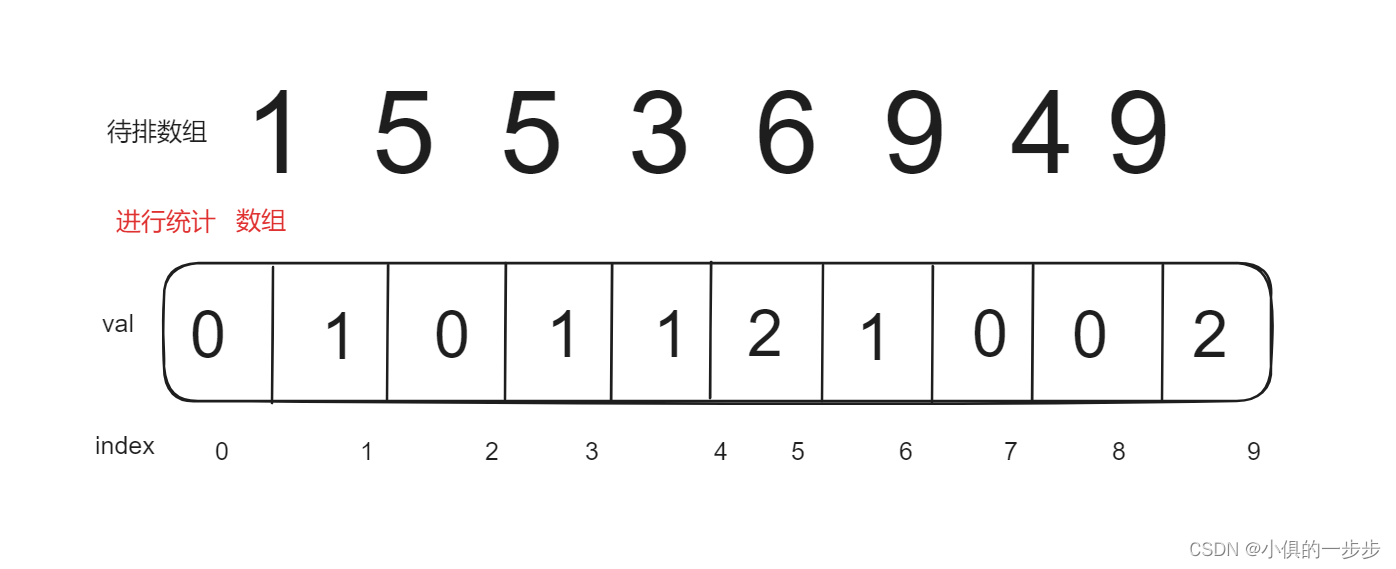
下面我们用一个问题来引出算法的时间复杂度这一概念。

该问题是，怎么去衡量一个程序（或者算法）的执行时间呢？就拿我们刚刚讲的排序算法来说，排序算法这么多，你又如何知晓哪一个排序算法执行的时间谁长谁短呢？

要想搞清楚该问题，那我们就不得不知道度量一个程序（或者算法）执行时间的两种方法了。

度量一个程序（或者算法）执行时间的两种方法

如何去度量一个程序（或者算法）的执行时间呢？目前来说，有两种方法可以度量一个程序（或者算法）的执行时间，它们分别是：

• 事后统计法；
• 事前估算法。

关于以上度量一个程序（或者算法）执行时间的两种方法，下面我给大家分别作一个详细的介绍。

事后统计法

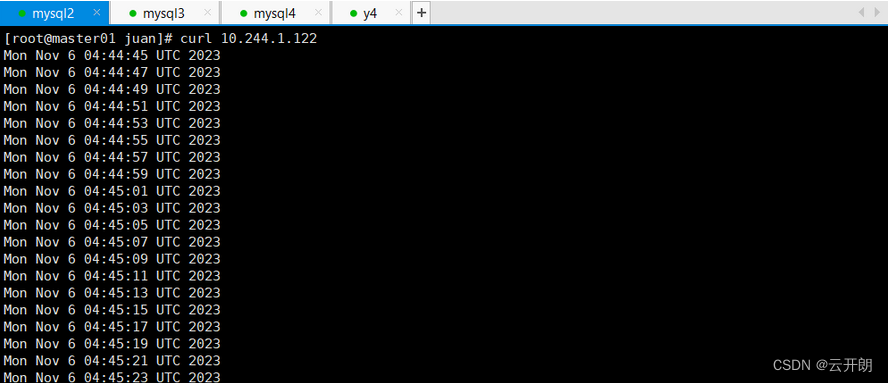
所谓事后统计法，就是指将一个程序直接运行过后，再来看它执行花费了多少时间。如果是要比较两个程序的执行时间，那就分别运行一下这两个程序，运行完过后，再来对它们的执行时间进行比较。

但是，我这里就要说但是了，虽然这种事后统计法可行，但是它有两个问题。

一是要想对设计的算法的运行性能进行评测，需要实际运行该程序。

有朋友可能想说，运行程序那就运行一下呗，有什么大不了的，但你有没有想过这样一个问题，就是该程序运行非常耗费时间，譬如我们设计了一个统计海量数据的算法，它运行完毕需要耗费十分钟，对该算法的运行性能进行评测时，你总不能傻傻地等待它运行十分钟吧！有这时间，干点啥不好呢！

二是所得时间的统计量依赖于计算机的硬件、软件等环境因素。

我们都知道一个程序它执行时间的长短，除了跟它本身有关之外，还与计算机的硬件、软件等环境因素有关，譬如运行程序的计算机内存足够大，CPU也足够强，那这就不能完全体现出该程序本身的优越性了。就拿A、B两个程序来说，如果A程序是运行在一号计算机上，B程序是运行在二号计算机上，那么你敢保证，若A程序执行时间短，则其算法就一定优于B程序所设计的算法吗？不一定吧，对不对，因为它俩都不在同一台计算机上运行，也即所依赖的计算机硬件不同，你咋个敢保证的嘛！

当然，如果你一定要用事后统计法，那也没人说你个不是，只是这儿你就得遵循这样一个前提了，即得要在同一台计算机的相同状态下运行，才能比较哪个算法速度更快。

OK，事后统计法讲完过后，接下来我就要来给大家讲解第二种度量一个程序（或者算法）执行时间的方法了，即事前估算法。

事前估算法

何谓事前估算法呢？事前估算法就是指通过分析某个算法的时间复杂度来判断哪个算法更优。

由此，算法的时间复杂度这一概念就被我们从这儿引出来了，正好呼应了文章的开头。

废话不多说，接下来我就来给大家详细讲解算法的时间复杂度这一概念，注意，这儿我讲解的篇幅可能会很长，因为我得给大家讲清楚如何推算一个算法的时间复杂度，以及常见的时间复杂度都有哪些，所以还请大家一定要耐着性子读完哟！

时间频度介绍及其特点

在给大家讲清楚算法的时间复杂度之前，我们得知道它里面的一个概念，即时间频度。

于是，接下来我就要来给大家简单介绍一下时间频度了，当然，其特点我也会给大家详细讲到。

基本介绍

何谓时间频度呢？

一个算法花费的时间是与算法中语句的执行次数成正比例的，也即哪个算法中语句执行次数多，它花费时间就多。而一个算法中的语句执行次数就被我们称之为语句频度或者时间频度。

注意，时间频度是用一个专门的符号来记的，即T(n)。

光这样给大家作基本介绍，我想大家恐怕也不会有什么形象的认识，就你都不知道时间频度它说的到底是个啥，所以下面我会举个例子再来给大家说明一下时间频度。

例如，现在我们要计算1~100所有数字之和，请问你该怎么做？问题非常简单，我想大家不假思索，就能很容易地设计出两种算法。

下面我们先来看第一种算法，即使用for循环来计算，代码如下：

int total = 0;
int end = 100;
// 使用for循环计算
for(int i = 1; i <= end; i++) {
    total += i;
}

这时，我就要请同学们思考一下了，上面这段代码它的一个时间频度究竟是多少呢？是n + 1，即T(n) = n + 1，其中n是以上程序的一个问题规模。

为什么以上程序的时间频度会是n + 1呢？按理说，应该是n才对啊，你上面程序中的for循环不是循环了100次吗，当问题规模n等于100的时候，确实是这样哈，但是你没发现以上程序中的for循环最后还得判断一次才能退出吗，所以咱们还得在n的基础上加个1，这样，以上程序的时间频度就变成了n + 1。不知道我这样说，大家能否看明白？

接着，我们再来看第二种算法，即直接计算，代码如下：

// 直接计算
total = (1 + end) * end / 2;

以上这段代码它的一个时间频度又是多少呢？是1，即T(n) = 1，因为一句话就计算出了1-100所有数字之和。而这也就是说，不管问题规模n有多大，你是1000也好，还是10000也好，都无所谓，只要是计算1~n所有数字之和，那么它的时间频度就都应该是1。

特点

下面我们就来看一下对于时间频度而言，它究竟有哪些特点。

常数项可以忽略

请大家先看如下这样一张表格，应该能看到我这儿有四个时间频度吧！

不知道大家发现没有，随着问题规模n的不断增大，T(n) = 2n + 20和T(n) = 2n这俩时间频度所代表的程序（或者算法）的语句执行次数是无限接近的，还有T(n) = 3n + 10和T(n) = 3n也是同一个道理。

下面，我们再来看一下下面这样一张图，即以上四个时间频度所对应的曲线走势图。

相信大家可以从上图中看到：

1. T(n) = 2n + 20和T(n) = 2n随着问题规模n的不断变大，执行曲线是无限接近的，也即常数项20是可以被忽略的；
2. T(n) = 3n + 10和T(n) = 3n随着问题规模n的不断变大，执行曲线也是无限接近的，同上，常数项10也是可以被忽略的。

由此，不难得出这样一个结论，即在统计一个程序（或者算法）的时间频度时，对于时间频度而言，常数项是可以被我们忽略的。

低次项可以忽略

请大家先看如下这样一张表格，应该能看到我这儿有四个时间频度吧！

不知道大家发现没有，随着问题规模n的不断增大，T(n) = 2n^2 + 3n + 10和T(n) = 2n^2这俩时间频度所代表的程序（或者算法）的语句执行次数是无限接近的，还有T(n) = n^2 + 5n + 20和T(n) = n^2也是同一个道理。

下面，我们再来看一下下面这样一张图，即以上四个时间频度所对应的曲线走势图。

相信大家可以从上图中看到：

1. T(n) = 2n^2 + 3n + 10和T(n) = 2n^2随着问题规模n的不断变大，执行曲线是无限接近的，也即3n + 10是可以被忽略的。注意，常数项10前面已经被我们忽略了。
2. T(n) = n^2 + 5n + 20和T(n) = n^2随着问题规模n的不断变大，执行曲线也是无限接近的，同上，5n + 20也可以被忽略。

由此，不难得出这样一个结论，即在时间频度的表达式里面，我们是可以忽略低次项的。

之所以这里我要苦口婆心地给大家讲解时间频度的特点，是因为它的这些特点会直接影响到我们后面时间复杂度的一个计算，要注意这点哟！

高次项的系数可以忽略

请大家先看如下这样一张表格，应该能看到我这儿有四个时间频度吧！

不知道大家发现没有，随着问题规模n的不断增大，T(n) = 3n^2 + 2n和T(n) = 5n^2 + 7n这俩时间频度所代表的程序（或者算法）的语句执行次数是无限接近的，但与上面不同的是，这会T(n) = n^3 + 5n和T(n) = 6n^3 + 4n可就不是同一个理了，随着问题规模n的不断增大，它俩所代表的程序（或者算法）的语句执行次数之比会无限地接近于一个常数，即6。

下面，我们再来看一下下面这样一张图，即以上四个时间频度所对应的曲线走势图。

相信大家可以从上图中看到：

1. 随着问题规模n的不断增大，T(n) = 5n^2 + 7n和T(n) = 3n^2 + 2n所表示的执行曲线会逐渐重合, 说明在这种情况下，它俩高次项的系数5和3是可以被忽略的；
2. 而T(n) = n^3 + 5n和T(n) = 6n^3 + 4n所表示的执行曲线则分离了，这说明时间频度最主要是跟多少次项有关系，也就是说对于时间频度而言，次方表示是非常非常关键的。

由此，不难得出这样一个结论，对于时间频度而言，高次项的系数是可以被我们忽略的，虽说如此，但有一点需要我们特别注意，就是立方项的系数是不可以被忽略的。

之所以这里我要苦口婆心地给大家讲解时间频度的特点，是因为它的这些特点会直接影响到我们后面时间复杂度的一个计算，要注意这点哟！

经过我上面详细的讲解，相信大家脑海中对时间频度这一概念已经有了一个清晰的认识，而有了这样一个基础之后，接下来我再来给大家讲解时间复杂度，相信大家就比较容易能接受了。

时间复杂度

有了时间频度这一概念之后，下面，我就来给大家介绍一下时间复杂度，当然，其计算方法我也会给大家讲到。

基本介绍

一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为一个不等于零的常数，则称f(n)是T(n)的同数量级函数。此时，我们就可以将T(n)记作Ｏ(f(n))，即T(n) = Ｏ(f(n))，而Ｏ(f(n))我们就称为算法的渐进时间复杂度，简称时间复杂度。当然，这个f(n)到底是一个什么样的表达式，咱们是要根据实际情况来决定的。

就拿我们上面刚刚讲过的T(n) = n + 1来说，假设此时有一个辅助函数f(n) = n，当n趋近于无穷大时，T(n)/f(n)的极限值是不是就相当于是f(n)/n啊，即1，那么这个时候，我们就说f(n)是T(n)的一个同数量级的函数，这样，T(n)就可以被我们简写成Ｏ(f(n))了，即Ｏ(n)，它就被我们称之为算法的渐进时间复杂度，简称时间复杂度。

相信经我这样一说，大家对时间复杂度这一概念应该有了一个基本的认识。

对时间复杂度有了一个基本的认识之后，下面我就要来给大家着重说明一个知识点了，即 T(n)不同，但时间复杂度有可能相同。

例如，T(n) = n^2 + 7n + 6和T(n) = 3n^2 + 2n + 2，用眼睛一扫，就知道这俩时间频度的表达式是不一样的，即T(n)不同，但是它俩对应的时间复杂度却相同，都是Ｏ(n²)。

为什么上面这俩时间频度对应的时间复杂度都是Ｏ(n²)呢？大家还记得前面我给大家讲时间频度时说过的话吗？即对于时间频度而言，常数项、低次项以及高次项的系数都是可以被我们忽略的。而又假设此时有一个辅助函数f(n) = n²，可以想见的是，当n趋近于无穷大时，T(n)/f(n)的极限值就是一个不等于零的常数（你甭管它是1还是几，说到底，它终究是一个不等于零的常数），因此，这个时候我们就可以用Ｏ(f(n))（即Ｏ(n²)）来表示上面这俩时间频度对应的时间复杂度了。

现在大家该回过味来了吧！

最后我还得说一嘴，上面我给大家苦口婆心地讲解时间频度，那可不是白讲的，你看，咱们在计算时间复杂度时，是不是就用到了它的三个特点啊，所以时间频度大家一定要认真理解清楚。

计算方法

大家看这样一个时间频度，即T(n) = n^2 + 7n + 6，请问它对应的时间复杂度是多少？

下面我就以上面这样一个案例来教教大家如何计算一个时间复杂度。

对于T(n) = n^2 + 7n + 6这样一个时间频度而言，我们是这样来计算它对应的时间复杂度的。

• 首先，用常数1代替运行时间中的所有加法常数。

  根据这条规则，T(n) = n^2 + 7n + 6很明显就被我们改造成了T(n) = n^2 + 7n + 1。

• 然后，在修改后的运行次数函数中，只保留最高阶项。

  也就是说，T(n) = n^2 + 7n + 1此时又得被我们改造成T(n) = n^2了。很显然，在此过程中，常数项1和低次项7n都被我们忽略了。

• 最后，去除最高阶项的系数。

  由于改造之后的T(n) = n^2其最高阶项的系数就是1了，所以去除最高阶项的系数之后，它仍旧是T(n) = n^2。

根据上面三条规则，很顺利地我们就能推算出T(n) = n^2 + 7n + 6所对应的时间复杂度了，即Ｏ(n²)。

同样，对于T(n) = 3n^2 + 2n + 2而言，我们也可推算出它对应的时间复杂度，也是Ｏ(n²)。

常见的时间复杂度

接下来，我们就来看一下算法里面常见的时间复杂度到底都有哪些。

这里我也甭废话了，直接列出来，如下所示，可以看到算法里面常用的时间复杂度有八个，当然，现实中肯定不止这些，所以这里我才说的是常用的或者常见的。

1. 常数阶，即Ｏ(1)；

2. 对数阶，即Ｏ(log₂n)；

   至于对数阶的底数是多少，是2还是3还是5还是10，这个你得根据具体算法而言。

3. 线性阶，即Ｏ(n)；

   线性阶就是说，随着问题规模n的不断增大，算法中的语句执行次数跟着做相应的变化。

4. 线性对数阶，即Ｏ(nlog₂n)；

   可以很明显看到，线性对数阶就是线性阶和对数阶相互结合起来的一种时间复杂度。

5. 平方阶，即Ｏ(n²)；

   双层for循环，其时间复杂度就是一个平方阶，即Ｏ(n²)。

6. 立方阶，即Ｏ(n³)；

   同上，三层for循环，其时间复杂度就是一个立方阶，即Ｏ(n³)。

7. k次方阶，即Ｏ(n^k)；

   同上，嵌套了k层的for循环，其时间复杂度就是一个k次方阶，即Ｏ(n^k)。

8. 指数阶，即Ｏ(2^n)；

   指数阶，那可就太猛了，后面我会借助一张图来对指数阶作一点说明，即我们应极力避免使用指数阶这种时间复杂度的算法。

清楚以上算法里面常用的时间复杂度之后，下面我给大家作两点说明。

我们先来看第一点说明，即常见的算法时间复杂度由小到大排序依次为：

Ｏ(1) < Ｏ(log₂n) < Ｏ(n) < Ｏ(nlog₂n) < Ｏ(n²) < Ｏ(n³) < Ｏ(n^k) < Ｏ(2^n)

随着问题规模n的不断增大，上述时间复杂度也随之不断增大，可以想见，算法的执行效率也会越来越低。

其实，这里还有一个时间复杂度我没有向大家说明，不知道有没有同学见过它，它就是Ｏ(n!)，上面我们说了指数阶这种时间复杂度就已经够猛了，但它比指数阶这种时间复杂度还猛，而这也就是说这种时间复杂度是最大的，所以如果加上Ｏ(n!)这个时间复杂度之后，那么常见的算法时间复杂度由小到大的排序就应该要变成下面这样子了，即：

Ｏ(1) < Ｏ(log₂n) < Ｏ(n) < Ｏ(nlog₂n) < Ｏ(n²) < Ｏ(n³) < Ｏ(n^k) < Ｏ(2^n) < Ｏ(n!)

只不过，Ｏ(n!)这种时间复杂度大家见的很少，所以这里我也就没有提及。现在，我在这里提了一嘴，那想必大家应该知道有这个玩意了吧！嘻嘻😂。知道这个玩意之后，那大家就应该明白使用Ｏ(n!)这种时间复杂度的算法是要极力极力极力进行避免的。

接着，我们再来看第二点说明，即我们应该尽可能避免使用指数阶这种时间复杂度的算法。

为什么我会这么说呢？大家请看下面这样一张图。

从上图中可以看到，表示指数阶这种时间复杂度的执行曲线有一个显著特点，就是在问题规模n不大的时候，它还是很平滑的，但当问题规模n达到11、12的时候，它就突然陡增了，你可以想象，当问题规模n达到15的时候，它可能已经陡增到哪儿去了啊，是不是快到遥远的天边去了，显然远远地超出了其他的时间复杂度。

由此便知，只要你使用了指数阶这种时间复杂度的算法，那么该算法的执行效率就一定会是非常低下的，因为随着问题规模n的不断增大，表示指数阶这种时间复杂度的执行曲线增长的实在是太TM迅猛了。

最后我还想说一嘴，就是我们在写代码的时候，能写时间复杂度为常数阶的代码就尽量写这样的代码，因为这种时间复杂度是最OK的，其次则就是对数阶了。大家还记得我们上面在求1~100所有数字之和时所设计的那两个算法吗？一个使用for循环来计算，一个直接计算，显然前者就没有后者的执行效率高，这是因为前者的时间复杂度是Ｏ(n)，而后者的时间复杂度则是Ｏ(1)。

常数阶，即Ｏ(1)

常见时间复杂度说完了过后，下面我分别来为每一个举一个例子，以便加深大家对它们的认识，因为光说这个时间复杂度啊，大家没有印象，如果只让大家听一耳朵，而不见见具体的案例，那怎么能行呢？

这里，我们先来看第一个常见的时间复杂度，即常数阶，Ｏ(1)。

何谓常数阶呢？常数阶就是无论你代码执行了多少行，只要是没有循环等复杂结构，那么这个代码的时间复杂度就都是Ｏ(1)。

例如，下面这样一段代码，其时间复杂度就是Ｏ(1)。

int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

注意：上述代码在执行的时候，它消耗的时间并不会随着某个变量的增长而增长，大家看，i等于1，它是执行五条语句，i等于200000，它也还是执行五条语句，是不是，因此无论这类代码有多长，即使它有几万、几十万行，那么都可以用Ｏ(1)来表示它的时间复杂度。

相信大家现在也都知道了，如果一个算法它的时间复杂度是Ｏ(1)，那么这个算法它就是一个最好的算法。

对数阶，即Ｏ(log₂n)

在讲对数阶之前，不妨我们先来回顾一下初中数学中对数的一个基本含义。

回顾完毕之后，我们来看一下下面这段代码。

int i = 1;
while(i < n) {
    i = i * 2;
}

可以看到，上述代码while循环里面，每次都是将i乘以了2，可以想见，乘完之后，i距离n肯定就会越来越近。假设循环x次之后，i就大于或者等于n了，此时这个循环势必就要退出，显然，此时2的x次方至少得等于n，换算出来便是x ≥ log₂n，也就是说当循环log₂n次以后，这个代码就结束了。

因此，上述代码的时间复杂度就是Ｏ(log₂n)，注意，Ｏ(log₂n)中的底数实际上是根据代码来决定的，由于上面while循环体内每次都是i乘以2，所以这儿我才写的是2这个底数，要是while循环体内每次都是i乘以3，那么代码的时间复杂度则就变成Ｏ(log₃n)了。

线性阶，即Ｏ(n)

线性阶很好理解，单层for循环代码的时间复杂度就是Ｏ(n)，例如，下面这段代码。

for(i = 1; i <= n; ++i) {
    j = i;
    j++;
}

上述这段代码，想必大家应该都知道for循环里面的代码会执行n遍吧，由此可见，它消耗的时间也会随着n的变化而变化，因此这类代码咱们都可以用Ｏ(n)来表示它的一个时间复杂度。

那有人知道上述这段代码的时间频度吗？是不是就是T(n) = n + 1啊，还有印象吧，前面我给大家讲过啊！

线性对数阶，即Ｏ(nlog₂n)

线性对数阶其实非常容易理解，因为如果将时间复杂度为Ｏ(log₂n)的代码循环n遍的话，那么它的时间复杂度就是n * Ｏ(log₂n)，也即Ｏ(nlog₂n)。例如，下面这样一段代码。

for(m = 1; m < n; m++) {
    i = 1;
    while(i < n) {
        i = i * 2;
    }
}

上述这段代码如果只看里面的while循环，是不是它的时间复杂度就是一个对数阶啊，但是它外面又用for循环套了一层，所以它又将会被循环n遍，这样，上述这段代码的时间复杂度就是Ｏ(nlog₂n)了。

其实，所谓的线性对数阶就是用线性阶去乘以一个对数阶，上述这段代码的时间复杂度就是这样推算出来的，大家应该能看出来吧！自然，线性对数阶这种时间复杂度肯定就要比上面讲的线性阶大了。

平方阶，即Ｏ(n²)

平方阶Ｏ(n²)就更容易理解了，如果把时间复杂度为Ｏ(n)的代码再嵌套循环一遍，那么它的时间复杂度就是Ｏ(n²)。

例如，下面这段代码就嵌套了2层n循环，因此它的时间复杂度就是Ｏ(n²)。

for(x = 1; i <= n; x++) {
    for(i = 1; i <= n; i++) {
        j = i;
        j++;
    }
}

如果此时将上述这段代码中的其中一层循环的n改成m，那么它的时间复杂度就应变成Ｏ(m * n)。

立方阶，即Ｏ(n³)

参考上面讲的平方阶，相信你一下子就搞明白了立方阶其实就相当于是一个三层n循环的代码的时间复杂度。

k次方阶，即Ｏ(n^k)

同上，这里不再赘述。

指数阶，即Ｏ(2^n)

关于指数阶，上面我就已给大家作了一点说明，即应该尽可能避免使用指数阶这种时间复杂度的算法。

至于其他的话嘛，我也不多说了，因为既然是要极力避免它，那再说它就有点不上路了，你说，对吧！

至此，常见的时间复杂度我就一个个地给大家详细讲解完了，相信经过我这样一个讲解，同学们再回过头来看这些所谓的常见时间复杂度，是不是相对来说就好理解了啊！毕竟每个我都举了一个案例来为大家进行了说明，你脑海中现在对它们没有一个比较形象的认识，那就太说不过了，这不是枉费了我一片苦心嘛？

平均时间复杂度和最坏时间复杂度

。。。