一、说明
深度学习如此有效,这真是一个谜。尽管有一些关于深度神经网络为何如此有效的线索,但事实是没有人完全确定,并且深度学习的理论理解是一个非常活跃的研究领域。
在本教程中,我们将以一种不寻常的方式触及问题的一个小方面。我们将让神经网络为我们绘制抽象图像,然后我们将解释这些图像,以便对幕后可能发生的事情有更好的直觉。此外,作为奖励,在本教程结束时,您将能够生成如下所示的图像(所有内容都少于 100 行 PyTorch 代码。请在此处查看随附的 Jupyter 笔记本):

我的神经网络长大后想成为一名画家。
二、这个图像是如何生成的?
该图像是由一个称为组合模式生成网络(CPPN)的简单架构生成的,我是通过这篇博客文章介绍的。在那篇博客文章中,作者通过用 JavaScript 编写的神经网络生成抽象图像。我的代码在 PyTorch 中实现了它们。
通过神经网络生成图像的一种方法是让它们一次性输出完整图像,如下所示,称为“生成器”的神经网络将随机噪声作为输入,并在输出层中生成整个图像(其中尺寸(宽*高)。
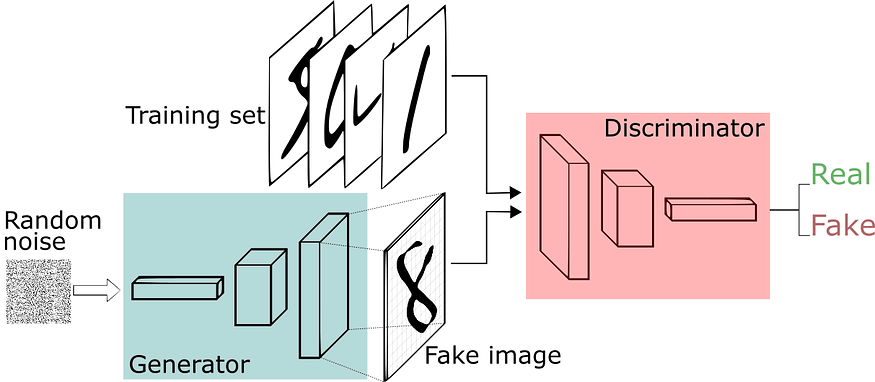
图片来自生成对抗网络简短介绍
与输出整个图像相反,CPPN(我们将要探索的架构)输出给定位置的像素颜色(作为输入输入)。

通过使用 TensorFlow 生成抽象模式的图像
忽略上图中的 z 和 r,请注意网络正在接收像素的x、y坐标并输出该像素应该是什么颜色(由c表示)。这种网络的 PyTorch 模型如下所示:
请注意,它需要 2 个输入,并有 3 个输出(像素的 RGB 值)。生成整个图像的方法是输入所需图像(特定尺寸)的所有 x,y 位置,并继续将这些 x,y 位置的颜色设置为网络输出的颜色。
三、神经网络实验
我第一次尝试运行上面看到的神经网络时,我最终生成了这些图像。

如果我有买家购买这件艺术品,我会立即卖掉它。
我花了很多时间摸不着头脑,想知道为什么无论我提供什么 x,y 位置作为输入,网络输出都是灰色的。理想情况下,这种情况不应该发生,因为对于如此深的网络。改变输入值应该改变输出值。我还知道,每次初始化神经网络时,由于其参数(权重和偏差)的随机初始化,它有可能生成全新的图像。但显然,即使经过几次尝试,我从神经网络中得到的只是这种灰色的粘稠物。为什么?
我的怀疑集中在所使用的特定激活函数上:tanh。也许后续层中的多个tanh序列将所有输入数字压缩到接近 0.5。在输出层(代表灰色)。然而,我关注的博客文章也使用了tanh。我所做的就是将博客的用 JavaScript 编写的神经网络转换为 PyTorch,*没有*任何更改。
我终于找到了罪魁祸首。这就是 PyTorch 在初始化新神经网络时初始化权重的方式。根据他们的用户论坛,他们使用从 -1/sqrt(N) 到 +1/sqrt(N) 范围内随机抽取的数字来初始化权重,其中 N 是层中传入连接的数量。因此,如果隐藏层 N=16,权重将从 -1/4 初始化到 +1/4。我对为什么这会导致灰色粘液的假设是因为权重来自一个小范围并且变化不大。
如果网络中的所有权重都在 -1/4 到 +1/4 之间,当乘以任何输入并相加时,也许会发生像中心极限定理这样的效果。
中心极限定理 (CLT) 规定,在某些情况下添加独立的随机变量,即使原始变量本身不是正态分布,它们的正确归一化总和也趋向于正态分布(非正式的“钟形曲线”)
回想一下后续层上的值是如何计算的。
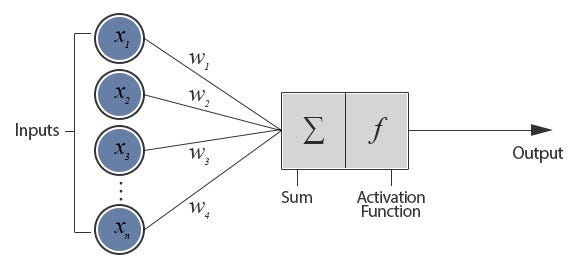
图片来自For Dummies — 我们都需要的神经网络简介!
在我们的例子中,第一个输入层有 2 个值 (x,y),第二个隐藏层有 16 个神经元。因此,第二层上的每个神经元都会获得 2 个值乘以从 -1/4 到 +1/4 得出的权重。将它们相加,然后在从激活函数tanh出发后,成为要传递到第三层的新值。
现在,从第二层开始,有 16 个输入要传递到第三层中的 16 个神经元中的每一个。想象一下,每个值都由z 表示。那么第三层每个神经元的值是:
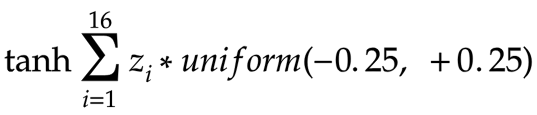
这是我们做出另一个猜测的地方。因为权重的方差较小(-1/4 到 +1/4),所以 z 的值(输入 x,y 乘以权重,然后通过tanh函数传递)也不会变化很大(因此将会类似)。所以方程可以看作:
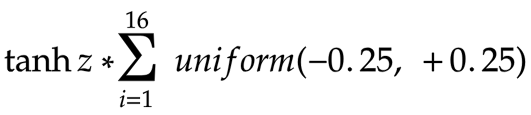
每个神经元从 -0.25 到 +0.25 的 16 个权重之和最有可能为零。即使在第一层中,总和不接近于零,网络的八层也为上述方程提供了足够的机会最终产生接近于零的值。因此,无论输入值 (x, y) 如何,进入激活函数的总值(权重总和 * 输入)始终接近零值,tanh 映射为零(因此,所有后续层中的值保持为零) )。
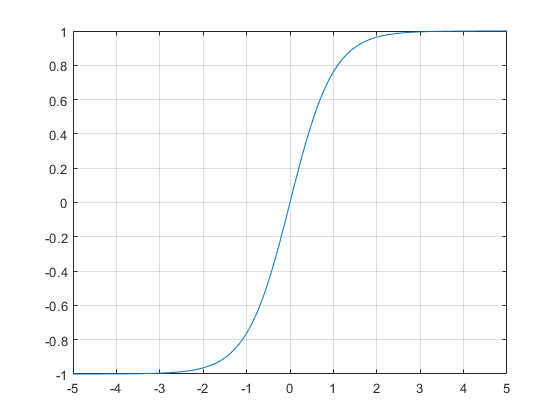
X 轴是 TanH 的输入,Y 轴是输出。请注意,0 被映射到 0。
颜色呈灰色是什么原因?这是因为 sigmoid(最后一层的激活函数)将传入值设为 0,并将其映射到 0.5(代表灰色,0 表示黑色,1 表示白色)。
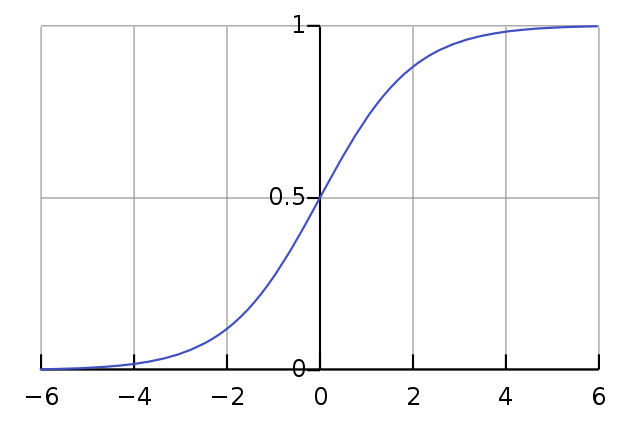
注意 Sigmoid 如何将 0 输入值映射到 0.5
四、如何修复灰色粘液?
由于罪魁祸首是权重的微小差异,我的下一步就是增加它。我更改了默认初始化函数,将权重从 -100 分配到 +100(而不是 -1/4 到 +1/4)。现在运行神经网络,这就是我得到的:

瞧!灰色粘液现在变成了一些颜色斑点。
现在,这是一些进展。我的假设是正确的。
但生成的图像仍然没有太多结构。这很简单。
这个神经网络在底层所做的就是将输入与权重相乘,将它们推入tanh,最后通过 sigmoid 输出颜色。既然我固定了权重,我可以固定输入以使输出图像更有趣吗?唔。
请注意,上面的图像是当我输入 X,Y 作为原始像素坐标时生成的,从 0,0 开始,到 128, 128(这是图像的大小)结束。这意味着我的网络从未将负数视为输入,而且由于这些数字很大(比如 X,Y 可能是 100、100),tanh要么得到一个非常大的数字(它被压缩为 +1),要么得到一个非常小的数字(它被压缩到-1)。这就是为什么我看到原色的简单组合(例如,0,1,1 的 R、G、B 输出代表您在上图中看到的青色)。
五、如何让图像变得更有趣?
就像在原来的博客文章(我正在关注的)中一样,我决定标准化 X 和 Y。因此,我不会输入 X,而是输入 (X/image_size)-0.5。这意味着 X 和 Y 的值范围为 -0.5 到 +0.5(与图像大小无关)。这样做我得到了以下图像:
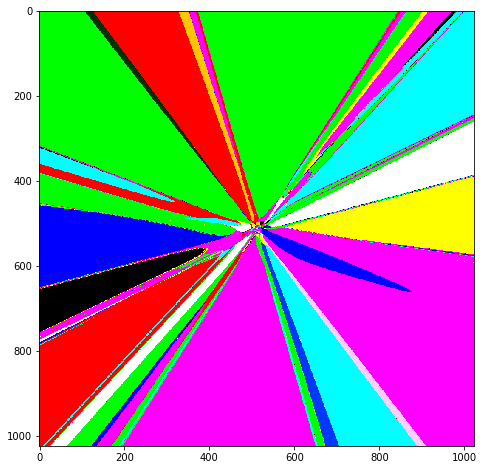
还有一些进步!
有趣的是,在上一张图像中,线条向右下角增长(因为 X、Y 值在增加)。此处,由于 X、Y 值已归一化并且现在包含负数,因此线条均匀地向外生长。
然而,图像仍然不够漂亮。
六、如何让图像变得更有趣?
如果你仔细观察,你会发现在图像的中间,似乎比边缘有更多的结构。这是数学之神的暗示,我们应该放大那里去发现美。
向图像中心放大的方法有以下三种:
- 生成大图像。由于像素坐标已标准化,我们可以简单地运行神经网络来生成更大的图像。之后,我们可以通过图像编辑工具放大中间,看看我们发现了什么。
- 将 X 和 Y 输入乘以少量(缩放系数),这将有效地实现与先前方法相同的效果(并避免我们在其余不感兴趣的区域上进行浪费计算)
- 由于输出是由输入 * 权重决定的,因此我们也可以通过将权重值从 -100、+100 减少到 +3、-3 等其他值来进行缩放(同时记住不要减少太多。记住)如果权重在 -0.25 到 +0.25 范围内,就会出现灰色粘液?)
当我采用第二种方法并将 X 和 Y 乘以 0.01 时,得到的结果如下:

我称之为神经蒙德里安!
当我采用第三种方法并将权重初始化为 -3 和 +3 之间时,这是我得到的图像。

你的心已经被震撼了吗?
七、更多实验
我将权重初始化更改为正态分布(平均值为 0,标准差为 1)并生成多个图像(通过随机初始化)。



当我删除所有隐藏层(仅输入到输出映射)时:

0 个隐藏层
当我只保留一个隐藏层(而不是默认的 8 个隐藏层)时:

1个隐藏层
当我将隐藏层数量加倍至 16 时:

16 个隐藏层,每个隐藏层 16 个神经元
正如您可以想象的那样,随着隐藏层数量的增加,图像变得更加复杂。我想知道如果我不将层数加倍,而是将层数保持不变 (8),但将每层的神经元数量加倍(从 16 个增加到 32 个),会发生什么。这是我得到的:

8 个隐藏层,每个隐藏层 32 个神经元
请注意,即使在上述两种情况下网络中的权重总数相似,但具有双倍层的网络比每层具有双倍神经元的网络更加像素化。像素表明在这些区域中函数变化剧烈,因此如果我们进一步放大,就会发现更多结构。而对于具有原始层数但每层神经元数量加倍的网络,功能非常平滑,因此不太“可缩放”。
当然,所有这些都是深度使神经网络更具表现力的另一种说法。正如《论深度神经网络的表达能力》论文所建议的那样:
计算函数的复杂度随着深度呈指数增长
这正是我们所看到的。万能逼近定理表明,理论上,一个足够大的神经网络即使只有一个隐藏层也可以表达任何函数。但实际上,网络越深,输入 -> 输出映射就越复杂。
八、毫无意义但很有趣的实验
如果我们将每层的神经元数量从 8 个增加到 128 个(增加一个数量级)会怎样?

神经波洛克!
如果我们从每个隐藏层 128 个神经元开始,但在每个后续层中逐渐将它们减半,如下所示。
这是我得到的:

这个看起来比其他的更“自然”。
人们可以进行“大量”更多实验并获得有趣的图像,因此我将其留在这里供您使用代码(Jupyter Notebook)。尝试更多架构、激活和层。如果您发现有趣的事情,请在 Twitter 上标记我或在 Medium 上发表评论,我将在我的网络中分享。
或者你可以将神经网络生成的图像与神经网络生成的哲学结合起来,并做出如下的东西:

我的神经网络是坚忍的。
就是这样。希望您能享受生成漂亮图像的乐趣。帕拉斯·乔普拉