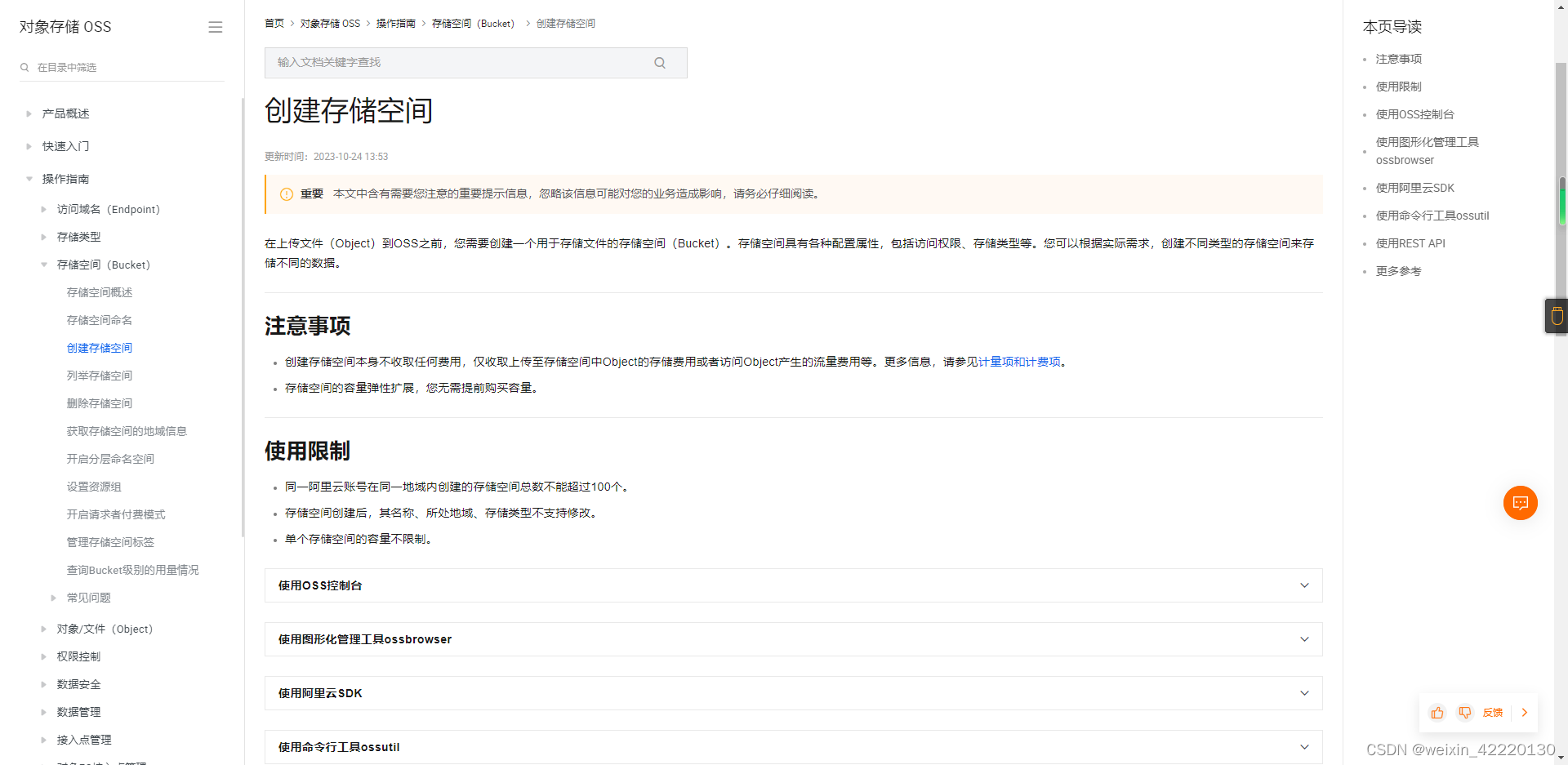
快速排序思想总结：

内附快排模版，可开袋即食。

学了一套快速排序的模版，接下来我说一下我的理解。

这套模板的思路是这样的，随机找到一个点，可以是数组中的左边界也可以是右边界，或者是数组中任何一个元素，为了方便计算和理解，这里将这个点设为左边界，并且叫做pivot。然后，去比较右边界和左边界的大小，先看右边界的值是否大于pivot的值，如果大于，则右边界一直往左走，当右边界的值小于pivot，则将右边界此时的值赋值给左边界。然后轮到左边界了，左边界也要比较和pivot的值的大小，如果小于pivot则一直往右走，如果大于，则将左边界的值赋值给右边界。循环这个操作，循环条件是左边界的指针大于右边界的指针。如果左边界的指针大于或者等于右边界的指针，就将此时的指针所指的值换成pivot。可以发现，我们第一趟函数走完，我们把大于pivot的放在pivot的右边，小于pivot的放在pivot的左边。此时很有可能pivot的左边或者右边还不是有序的，所以我们要继续递归执行这个函数，继续去排序pivot的左边和右边，文章的快排模版差不多是这个意思。

    public static void quickSort(int[] n,int start,int end){
        if(start>end) return;
        int left = start,right = end;
        int pivot = n[left];
        while(left<right){
            while(left<right&&n[right]>=pivot){
                right--;
            }
            if(left<right){
                n[left] = n[right];
            }
            while(left<right&&n[left]<=pivot){
                left++;
            }
            if(left<right){
                n[right] = n[left];
            }
            if(left>=right){
                n[left] = pivot;
            }
        }
        quickSort(n,start,right-1);
        quickSort(n,right+1,end);
    }