以下文中的,例如 s_1 为 s下角标1。面试加油!
- 控制系统的三要素:稳准快。稳,系统最后不能震荡、发散,一定要收敛于某一个值;快,能够迅速达到系统的预设值;准,最后稳态值和预设值的差比较小。
- 简要介绍身边的反馈系统:温度控制系统,温室大棚,锅炉是执行器件产生热量,传感器实时监测温度并反馈到控制器中,经过运算若低于温度则锅炉持续升热,反之同样。
- 控制系统的数学模型:在时域上可以用微分方程,在频域在复频域上用传递函数,方框图、信号流图。
- 传递函数是什么:在零初始条件下(系统没有储能的情况下,系统的输出信号完全由系统的输入信号引起),系统的输出拉氏变换比上输入的拉氏变换即为传递函数。
- 惯性系统(一阶系统)有哪些参数,分别作用是啥:只有一个参数,时间常数T,对于一阶系统可以调节快速性和稳定性。一阶系统没有超调量。看T的时间常数大小来判断快速性,T越大,快速性越差。
- 二阶系统有哪些时域的指标参数,分别定义和作用是啥:(1)延迟时间 t d :指输出响应第一次达到稳态值50%所需的时间。(2)上升时间 t_r :指输出响应第一次上升到稳态值所需要的时间。对于欠阻尼二阶系统,通常采用由0上升到稳态值的100%所需的时间;对于过阻尼系统,通常采用由稳态值的10%上升到稳态值的90%所需的时间。(3)峰值时间 t_p :指输出响应超过稳态值而达到第一个峰值 c{max}=c(t_ p) 所需的时间。(4)调节时间(或称过渡过程时间) t _s :指当c(t)和c(∞)之间误差达到规定允许范围(c(∞)的±5%或±2%),并且以后不再超出此范围所需的最小时间。(5)最大超调量(简称超调量) σ_p :系统响应的最大偏离量与终值的差与终值比的百分数。
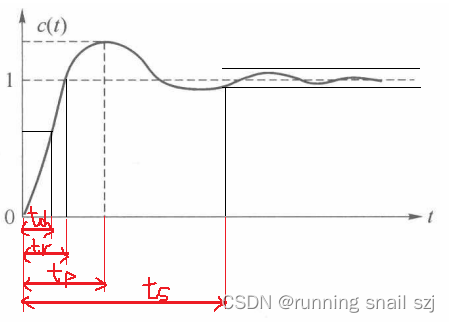
- 二阶系统的阻尼比、无阻尼自振角频率对常见指标的影响:典型二阶系统——弹簧阻尼系统分析。
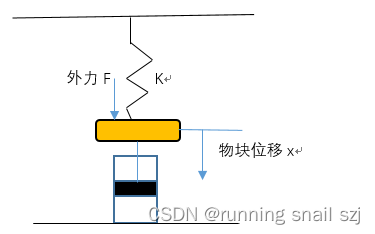
Wn为无阻尼振荡频率,反应弹簧的劲度系数,Wd为阻尼振荡频率,阻尼比反应阻尼系数与劲度系数的关系。Wn一定时:
阻尼比 ξ<0 的二阶系统是不稳定的,系统的动态过程为发散正弦震荡或单调发散的形式;
阻尼比 ξ=0 ,则特征方程有一对纯虚根,s_1,2=±jω_n,对应于s平面虚轴上一对共轭极点,可以算出系统的阶跃响应为等幅振荡,此时系统为无阻尼情况;
阻尼比 0<ξ<1 ,则特征方程有一对具有负实部的共轭复根,s_1,2=-ξω_n±jω_n √(1-ξ^2 ),对应于s平面左半部分的共轭复数极点,相应的阶跃相应为衰减震荡过程,系统为欠阻尼情况;
阻尼比 ξ=1 ,则特征方程有两个相等的负实根,s_1,2=-ω_n,对应于s平面负实轴上的两个相等实极点,相应的阶跃响应非周期地趋于稳态输出,此时系统为临界阻尼情况;
阻尼比 1<ξ ,则特征方程有两个不相等的负实根,s_1,2=-ξω_n±ω_n √(ξ^2-1),对应于s平面负实轴上的两个不等实极点,相应的单位阶跃响应也是非周期地趋于稳态输出,但响应速度比临界阻尼情况缓慢,因此称为过阻尼状态。
可以通过这个例子,阻尼越大弹簧越不震荡,容易得出:阻尼ξ和阻尼振荡频率Wd越大,上升时间、调节时间、峰值时间、超调量都越小;峰值时间等于阻尼振荡周期的一半,t=Π/Wd,与阻尼ξ无关;超调量只与阻尼比有关。 - 高阶系统的等效,如何分析一个高阶系统,也即如何找到高阶系统的主导极点?:找到最能影响系统性能的极点,然后近似当成二阶系统来对待。闭环主导极点为距离虚轴最近的闭环极点。拉普拉斯变换,拉普拉斯的衰减因子e^(-δt),δ越大经过相同时间衰减的越少 。
- 稳定性判据有哪些:分为时域和频域回答。时域:劳斯稳定判据(判断系统特征根是否全部位于s左半平面,有全0行就用上一行系数构造辅助方程并对s求导,得到的系数替代得到完整的劳斯计算表)、赫尔维兹稳定性判据。频域:奈奎斯特稳定性判据、对数稳定性判据。 频域先省略后补
- 稳态误差,要想使二型系统的稳态误差输出为常数,则输入信号满足什么条件:先分系统类型,再用终值定理法计算。。。。。。。。