一、划分基本块、画流图
- 找基本块的入口:一共有三类入口:①代码段的第一个指令;②条件跳转和无条件跳转的目标语句;③条件跳转语句的下一条语句;
- 根据划分的入口画流图,一个基本块的区间:从入口开始,至到遇到下一个入口结束;
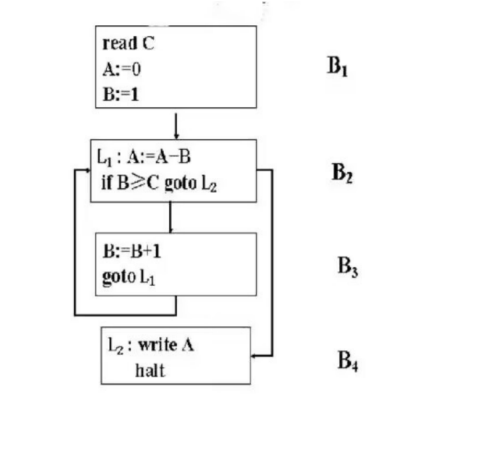
例题1

分析
- 首先根据上面的3类找基本块入口的方法,把基本块入口找出来;

- 根据划分的入口画流图,一个基本块从入口开始,至到遇到下一个入口结束;
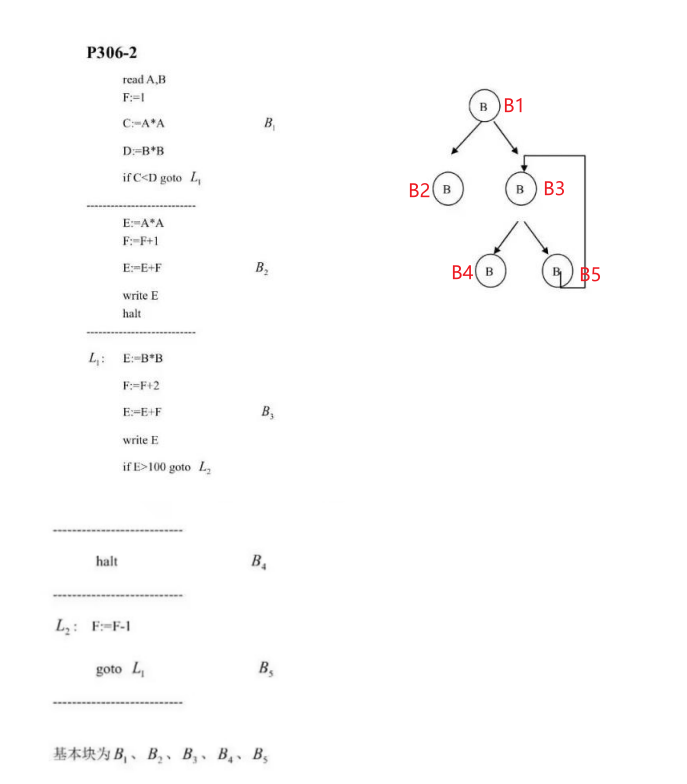
例题2

分析
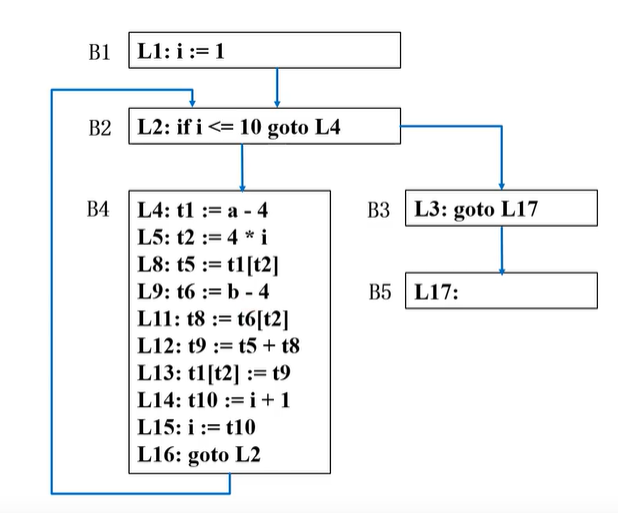
- 首先根据上面的3类找基本块入口的方法,把基本块入口找出来;一共5个基本块:B1、B2、B3、B4、B5;

- 根据划分的入口画流图,一个基本块从入口开始,至到遇到下一个入口结束;
二、基本块优化
例题1

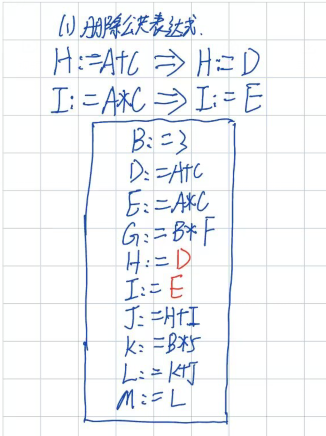
(一)、删除公共子表达式
删除前面已经计算过得、公共子表达式;由于A+C、A*C已经计算过,故将H=D,I=E;
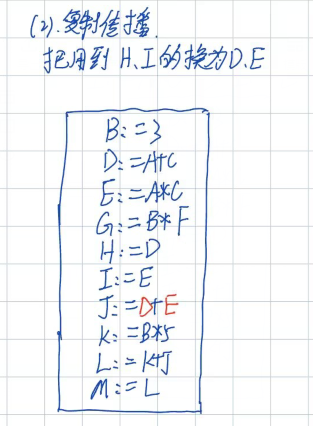
(二)、复制传播
把后面用的H、I的换为根(源头),H的源头是D,那么把下面用到H的换成D;I的源头是E,那么把下面用到I的换成E;
(三)、删除死代码
把没用的代码直接删掉;H、I已经没用任何用处了
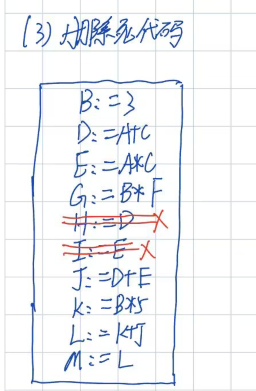
(四)、根据题目要求再优化

常量B,可以直接删掉,把用到B的都替换成3即可;然后只写G、L、M用到的基本块,其余的不用写;

例题2
图片来源于:Bilibili 中间代码优化习题讲解,讲的挺不错的,可以去看看;

三、循环优化
例题1
这个例题就是从Bilibili 中间代码优化习题讲解里截取的,挺经典;
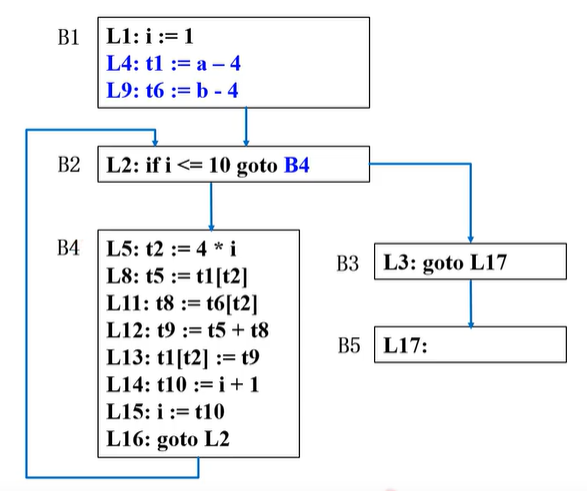
(一)、代码外提
把循环中,一直不变的量(常量)移出循环,可以放在循环的上一个基本块中;
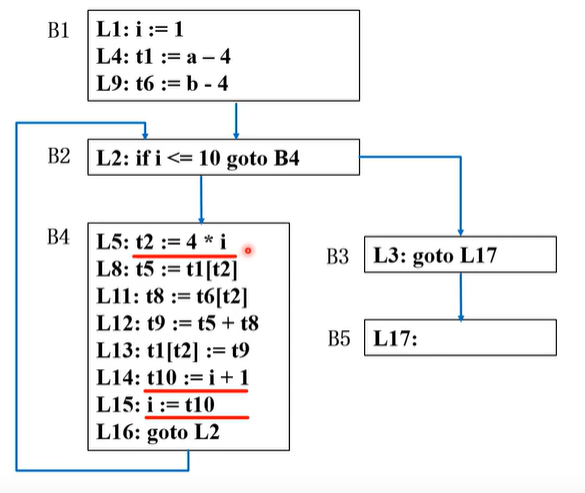
(二)、归纳变量强度削弱
- 通过循环结束if判断条件(i<=10),以及代码块( i 每次+1),可以发现 i 就是基本归纳变量;那么与i(基本归纳变量)相关的t2、t10就是归纳变量;
- 注意基本归纳变量 和 归纳变量是两个东西;
- 然后削弱归纳变量(把 i 通过别的方式替换掉),t2=4*i,乘法可以削弱为加法 变为 ==》t2=t2+4;然后那么t2就需要初始化,所以在B1将有一个t2=4 * i(i起始为1)的初始化;
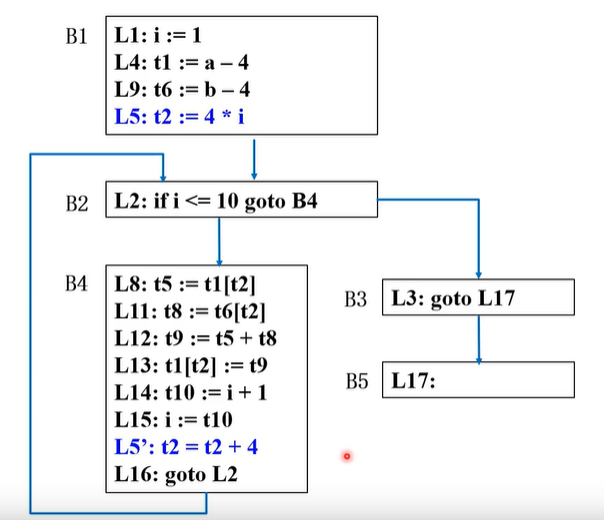
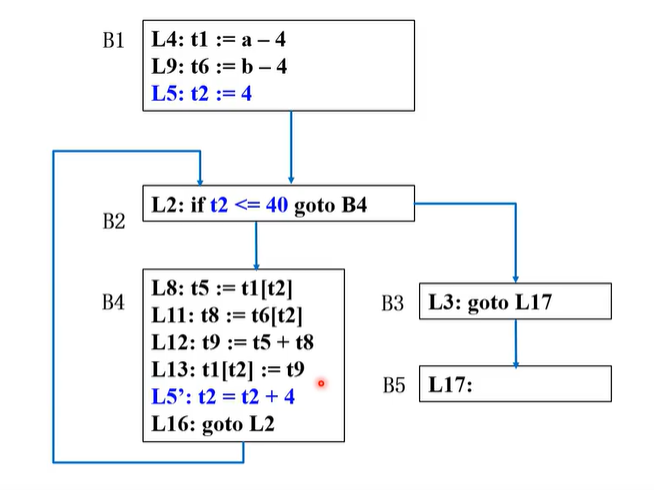
(三)、删除基本归纳变量
- 上面已经削弱了归纳变量,那么现在可以删除基本归纳变量 i,以及更换或删除和 i 相关的条件;
- 由于循环结束条件是i<=10,那么就是t2加10次4,那不就是t2=40为临界条件,所以把i<=10改为t2<=40;
- 所有与基本归纳变量 i 相关的t10也可以删了(t10的作用理解为for循环的i++);
- 并且B1中把常量1代入4*i,可以理解为:合并已知量;
例题2

分析
首先观察四元式程序,发现不用进行基本块优化,那么就可以直接通过上面的循环优化的步骤来做这个题;
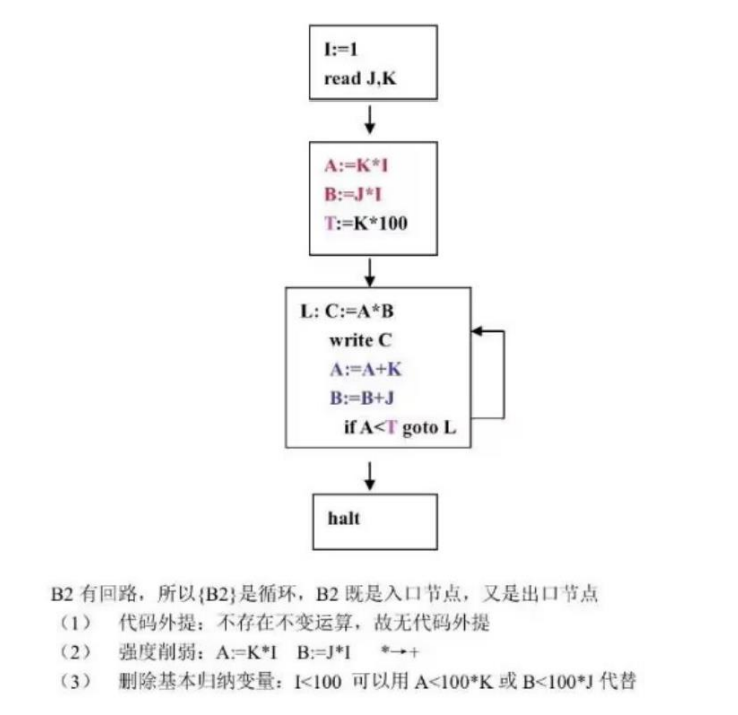
(一)、归纳变量强度削弱
- 可以发现循环体没有常量,所以省去第一步,直接进行第二步,归纳变量的削弱;
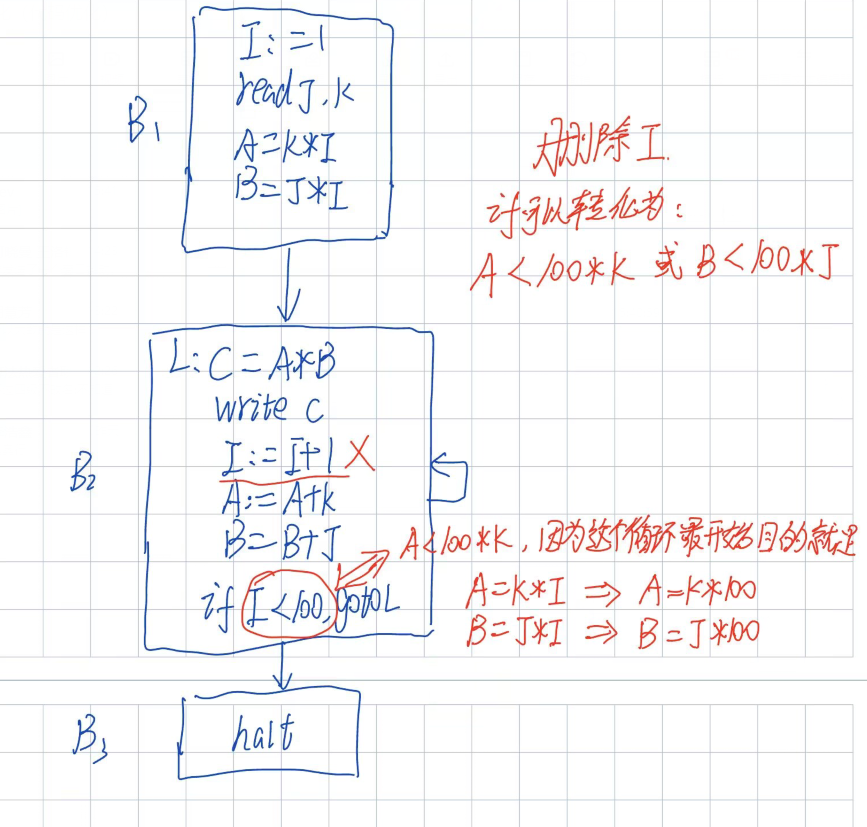
- 然后一个比较重要的规律:像 A=K*I 都可以转化为自身+=一个非I的数;比如此题的A=K*I,可以转换为A=A+K,因为K * I就相当于 I个K的和赋给A,等价于 A自身+=K,这样+= I次即可;需要记得初始化那些削弱后的归纳变量;
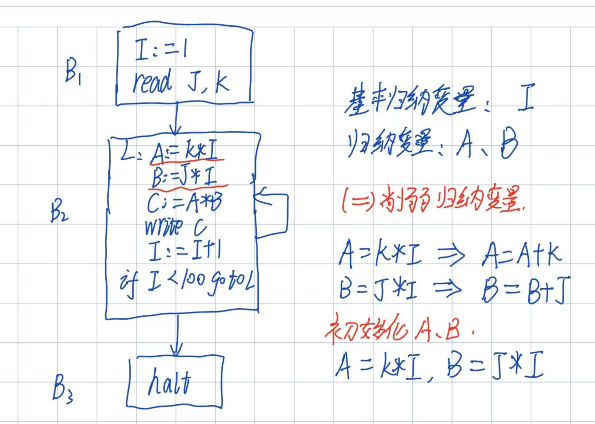
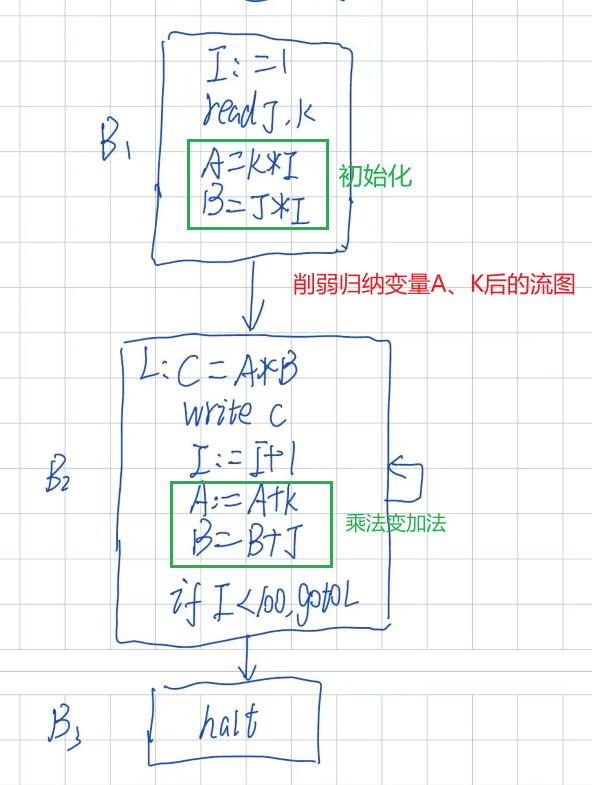
(二)、删除基本归纳变量 I
- 关于新的循环结束条件,最简单的方法就是看原程序的目的;所以循环结束条件可以是A<K * 100,也可以是B<J * 100;
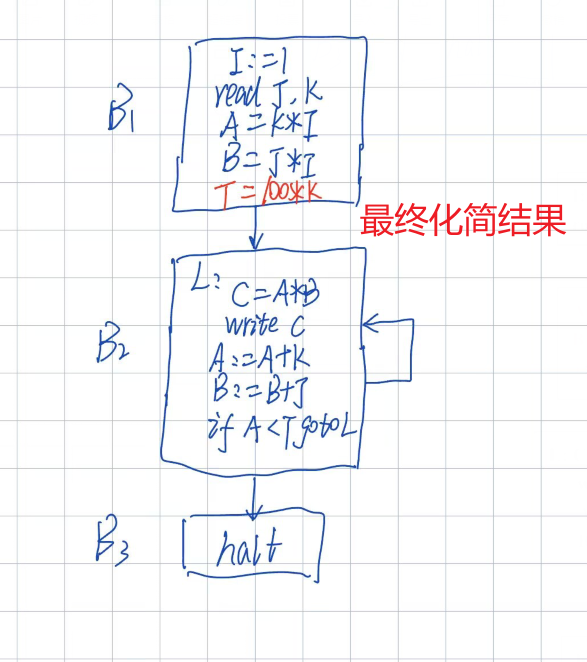
- 由于此题仅仅要求对循环进行优化,所以最后I=1的初始值还保留着,也可以像上面把常量I=1代入K*I,这里就不画蛇添足了;
- 然后我把K*100封装一个变量T了,然后代码外提部分我直接放在基本块1了,答案那样新开一个基本块也是一样的;

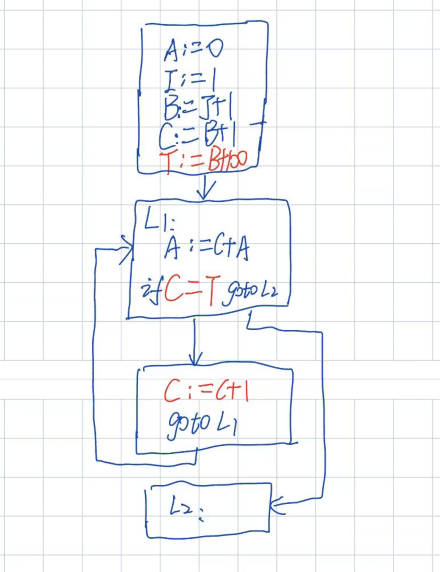
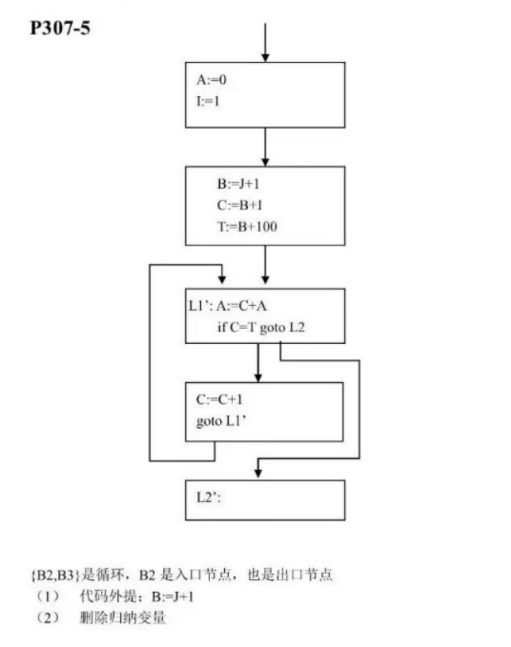
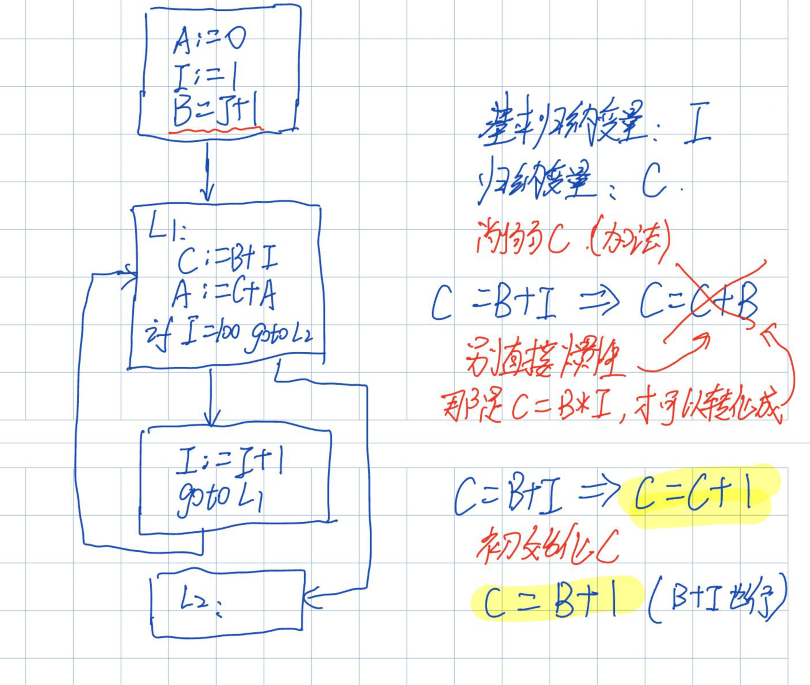
例题3

分析
首先观察四元式程序,发现不用进行基本块优化,那么就可以直接通过上面的循环优化的步骤来做这个题;
(一)、代码外提
B=J+1与循环无关,那么直接提出去即可;
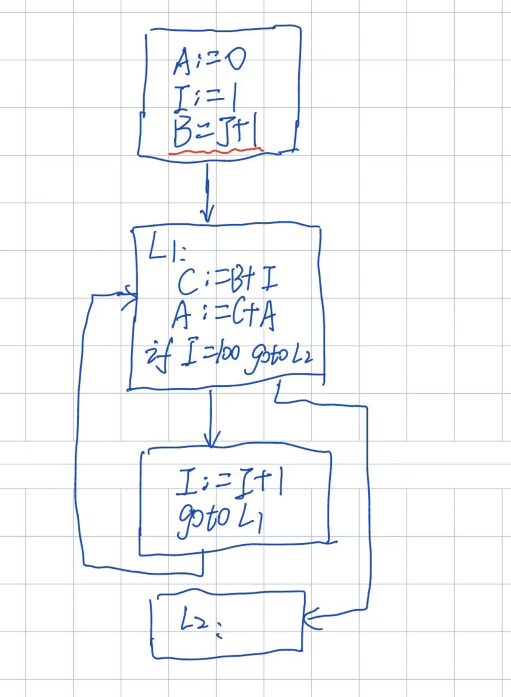
(二)、归纳变量强度削弱
- 需注意此题的归纳变量C,C=B+I,这里是加法,就不能像上面例题1、2直接转化本身 +=K;
- 可以发现每次C=B+I,每次的值都是,也就是C在B的基础上,每次加个1,所以 C赋个初值C=B+1,然后每次C=C+1,正好可以把I=I+1替换掉;
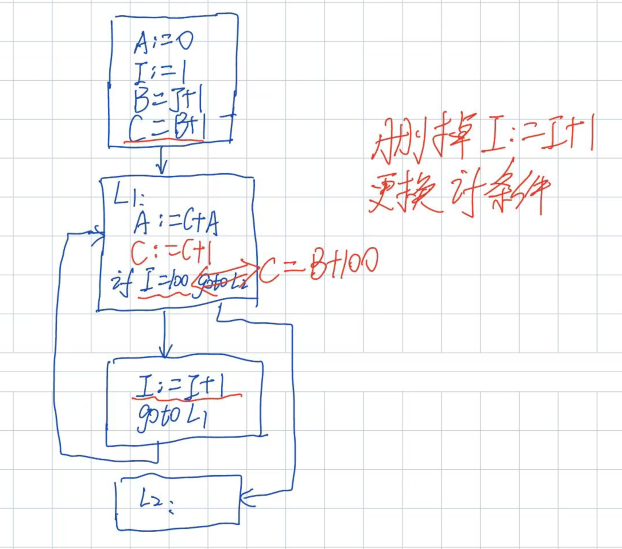
(三)、删除基本归纳变量 I
- 通过分析原程序,新的循环结束条件,是C=B+100;封装一个T=B+100,那循环结束就是C=T;