树与二叉树(遍历)

news2025/1/10 23:33:32

一、树

树结构是一种非常重要的非线性数据结构，该结构中的一个数据元素可以有两个或者两个以上的直接后继元素。

1、树的定义

树是由 n(n>=0)个有限结点组成一个具有层次关系的集合，当 n=0时称为空树，当 n>0时称为非空树。
对于非空树来说，它有且仅有一个称之为根的结点；除了根结点外的其余结点可分为 m(m>=0)多个互不相交的有限集T1，T2，…，Tm，其中每一个T集合本身又是一棵树，并且称为根结点的子树。

树的定义时递归的，它表明了树本身的固有特性，即一棵树由若干棵子树构成，可子树又由更小的子树构成。

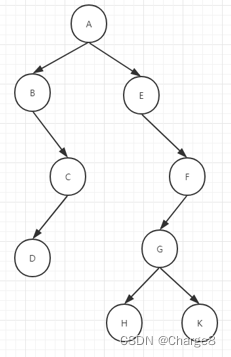
树结构示意图如下（来自网络）：
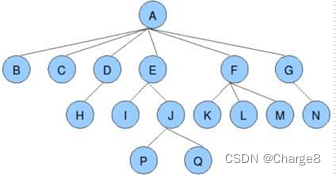
在这里插入图片描述

树具有的特点：

  • 1）树里面的元素称为结点（node）
  • 2）没有父节点的结点称为根结点（root）
  • 3）每一个非根结点有且只有一个父结点
  • 4）除了根结点外，每个子结点可以分为多个不相交的子树。

2、树的基本概念

若一个结点有子树，那么该结点称为子树根的“双亲”，子树的根称为该结点的“孩子”。有相同双亲的结点互为“兄弟”。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。

  • 结点：树里面的一个独立单元（元素）。如上图中 A、B等。
  • 父子关系：结点之间相连的边。
  • 子树：当结点大于 1时，其余的结点分为的互不相交的集合称为子树
  • 叶子结点：度为 0的结点称为叶子或终端结点。
  • 非终端结点：度不为 0的结点称为非终端结点或分支结点。除根结点外,非终端结点也称为内部结点。
  • 双亲和孩子：某结点的子结点称为该结点的孩子；该结点称为孩子的双亲。
  • 兄弟：具有同一个双亲的孩子结点称为兄弟结点。
  • 堂兄弟：双亲在同一层的结点互为堂兄弟。
  • 子孙：以某结点的子树上任意一个结点都为该结点的子孙。
  • 祖先：从根到该结点的双亲所经过的所有结点称为该结点的祖先。
  • 森林：由 m（m>=0）棵互不相交的树的集合称为森林。对森林加上一个根，森林即成为树；删去根，树即成为森林。
  • 有序树和无序树：如果树中节点的各子树看成从左至右是有次序的不能互换，则称该树为有序树，否则称为无序树。

还有几个很重要的概念：

  • 结点的度：一个结点拥有子树的个数称为该拥有的度。如上图中：A有 4个度，D有 1个度。
  • 树的度：树中最大的结点的度即为树的度。如上图中树的度为A节点的度为 4。
  • 层次：从根结点开始定义，根结点为第一层，树中任一结点层次为其双亲层次加 1。
  • 结点的高度：结点到叶子结点的最长路径
  • 树的高度：根结点的高度
  • 结点的深度：根结点到该结点的边个数
  • 树的深度：树中节点的最大层次
  • 结点的层数：结点的深度加 1。

二、二叉树

在树形结构中最重要的就是二叉树，很多经典的算法与数据结构其实都是通过二叉树发展而来。

1、二叉树的定义

二叉树是由 n(n>=0)个结点的有限集，当 n=0时称为空树，当 n>0时称为非空树。
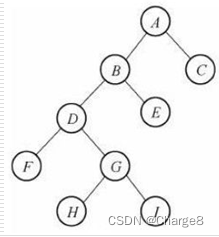
对于非空树来说，它有且仅有一个称之为根的结点；除了根节点外的其余节点可分为两个互不相交的子集 T1和 T2，分别称为 T的左子树和右子树，且 T1和 T2本身也是二叉树。

二叉树与树的区别：

  • 二叉树的每个节点至多只有两颗子树。
  • 二叉树是有序树，有左右子树之分。

在这里插入图片描述

2、二叉树的性质

  • 性质1：二叉树第i层上的结点数目最多为2i-1(i>=1)
  • 性质2：深度为k的二叉树至多有(2^k)-1个结点（k>=1）
  • 性质3：包含n个结点的二叉树的高度至少为(log2n)+1
  • 性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1

性质4的证明：
证明：因为二叉树中所有结点的度数均不大于2，不妨设n0表示度为0的结点个数，n1表示度为1的结点个数，n2表示度为2的结点个数。三类结点加起来为总结点个数，于是便可得到：n=n0+n1+n2 (1)
由度之间的关系可得第二个等式：n=n00+n11+n2*2+1即n=n1+2n2+1 (2)
将（1）（2）组合在一起可得到n0=n2+1

3、二叉树的分类

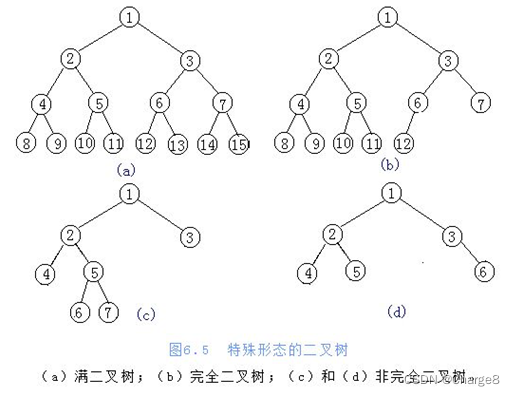
二叉树有几个特殊的分类如下：

3.1 满二叉树

定义：高度为h，并且由2h-1个结点组成的二叉树，称为满二叉树。即：除叶子结点外，每个结点都有左右两个子结点。

3.2 完全二叉树

定义：一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下层的叶结点集中在靠左的若干位置上，这样的二叉树称为完全二叉树。即：除最后一层外，其他的结点个数必须达到最大，并且最后一层结点都连续靠左排列。

特点：

  • 叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。
  • 一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

3.3 非完全二叉树

除了上面两种的二叉树，剩下的可以认为属于非完全二叉树。

在这里插入图片描述

4、二叉树的存储

1）基于数组存储：
利用数组下标。假设A为 i，则 B=2i, C=2i+1，依次类推，如果没有的结点，数组的位置需要保留。
如果针对非完全二叉树来使用数组来存储的话会浪费很多空间，那么就需要使用链表存储。
2）基于链表存储。
注意：数组的性能是高效的，并且不需要开额外的指针。所以如果是一课完全二叉树的话我们就可以用数组来实现。

三、二叉树的遍历

1、二叉树的遍历

1.1 先序遍历(PreOrder)

先（前）序遍历：访问根结点的操作发生在遍历其左右子树之前

具体操作：若二叉树非空，则依次执行如下操作：

    1. 访问根结点；
    1. 遍历左子树；
    1. 遍历右子树。

1.2 中序遍历( InOrder)

中序遍历：访问根结点的操作发生在遍历其左右子树之中（间）。

具体操作： 若二叉树非空，则依次执行如下操作：

    1. 遍历左子树；
    1. 访问根结点；
    1. 遍历右子树。

1.3 后序遍历(PostOrder)

后序遍历：访问根结点的操作发生在遍历其左右子树之后。

具体操作： 若二叉树非空，则依次执行如下操作：

    1. 遍历左子树；
    1. 遍历右子树；
    1. 访问根结点。

1.4 层次遍历

层次遍历即为从上到下，从左到右依次访问二叉树的每个结点。

实现思路：用一个队列保存被访问的当前节点的左右孩子以实现层序遍历。

  • 1）我们定义一个队列，先将根结点入队；
  • 2）当前结点是队头结点，将其出队并访问；
  • 3）若当前结点的左结点不为空将左结点入队；若当前结点的右结点不为空将其入队即可。

2、代码示例

在这里插入图片描述
1）基于链表存储二叉树

@Data
@AllArgsConstructor
@NoArgsConstructor
public class BinaryTree {

	// 结点元素
	private String data;
	private BinaryTree left;
	private BinaryTree right;

	/**
	 * 输出结点元素
	 * 
	 * @param node
	 */
	public void print(BinaryTree node) {
		System.out.print(node.getData());
	}

	/**
	 * 前序遍历: 根(输出) 左 右 <br/>
	 * 时间复杂度：O(2*n) => O(n);
	 * 
	 * @param root
	 */
	public void pre(BinaryTree root) {
		if (root == null) {// 空树
			return;
		}
		print(root);
		if (root.getLeft() != null) {
			pre(root.getLeft()); // 认为是子树,分解子问题
		}
		if (root.getRight() != null) {
			pre(root.getRight());
		}
	}

	/**
	 * 中序遍历：左 根(输出) 右
	 * 
	 * @param root
	 */
	public void in(BinaryTree root) {
		if (root == null) {// 空树
			return;
		}
		if (root.getLeft() != null) {
			in(root.getLeft()); 
		}
		print(root);
		if (root.getRight() != null) {
			in(root.getRight());
		}
	}

	/**
	 * 后序遍历：左 右 根(输出)
	 * 
	 * @param root
	 */
	public void post(BinaryTree root) {
		if (root == null) {// 空树
			return;
		}
		if (root.getLeft() != null) {
			post(root.getLeft()); 
		}
		if (root.getRight() != null) {
			post(root.getRight());
		}
		print(root);
	}

	/**
	 * 层次遍历
	 * 
	 * @param root
	 * @return
	 */
	public List<String> levelOrder(BinaryTree root) {
		List<String> levelList = new ArrayList<>();
		if (root == null) {// 空树
			return levelList;
		}

		// 定义一个队列
		Queue<BinaryTree> queue = new LinkedList<>();
		queue.offer(root);// offer方法表示添加元素到队尾
		while (!queue.isEmpty()) {
			BinaryTree temp = queue.poll();// poll方法删除队头元素
			levelList.add(temp.data);
			if (temp.left != null) {
				queue.offer(temp.left);
			}
			if (temp.right != null) {
				queue.offer(temp.right);
			}
		}
		return levelList;
	}

}

2）测试

    public static void main(String[] args) {
        // 插入数据小技巧，先插入叶子结点
        BinaryTree D = new BinaryTree("D", null, null);
        BinaryTree H = new BinaryTree("H", null, null);
        BinaryTree K = new BinaryTree("K", null, null);
        BinaryTree C = new BinaryTree("C", D, null);
        BinaryTree G = new BinaryTree("G", H, K);
        BinaryTree B = new BinaryTree("B", null, C);
        BinaryTree F = new BinaryTree("F", G, null);
        BinaryTree E = new BinaryTree("E", null, F);
        BinaryTree A = new BinaryTree("A", B, E);

        BinaryTree binaryTree = new BinaryTree();
        System.out.println("前序遍历：");
        binaryTree.pre(A);
        System.out.println();
        
        System.out.println("中序遍历：");
        binaryTree.in(A);
        System.out.println();
        
        System.out.println("后序遍历：");
        binaryTree.post(A);
        System.out.println();
        
        System.out.println("层次遍历：");
        List<String> levelOrderList = binaryTree.levelOrder(A);
        System.out.println(levelOrderList);
    }

在这里插入图片描述

– 求知若饥，虚心若愚。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/118405.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

水上交通AIS常见问题解决方案

水上交通AIS常见问题解决方案

水上交通AIS常见问题解决方案 AIS无信号的几种情况 情况一&#xff1a;AIS未开启。 解决方法&#xff1a;开启AIS设备。 情况二&#xff1a;AIS开启但MMSI码和证书不一致。 解决方法&#xff1a;船长向直属海事部门申请MMSI码&#xff0c;并请专业人员将正确的MMSI码写入AIS设…
阅读更多...
数据结构之堆的实现以及实现堆排序和建堆解决Top K问题

数据结构之堆的实现以及实现堆排序和建堆解决Top K问题

文章目录前言1.堆的相关介绍1.什么是堆2.堆的结构2.堆的相关接口具体实现1.堆的声明和堆的初始化2.堆插入数据和删除数据3.堆的其他函数接口3.堆的实际运用1.建堆算法2.堆的应用之堆排序3.堆解决Top k问题4.总结前言 之前对树的相关知识概念进行了简单介绍&#xff0c;本文将实…
阅读更多...
odps-jdbc提交MaxCompute数据源SQL报错HTTP/1.0 is not allowed

odps-jdbc提交MaxCompute数据源SQL报错HTTP/1.0 is not allowed

概述 最近负责的一款数据产品。有个功能&#xff1a;选择某个数据源&#xff0c;比如阿里云的MaxCompute数据源&#xff0c;然后手写SQL&#xff0c;点击自动生成字段&#xff08;即获取前置SQL里的查询字段。前置SQL可以有drop then create table动作子句&#xff0c;但是最后…
阅读更多...
【PS-选区速成】快速选择工具、魔棒工具、对象选择工具

【PS-选区速成】快速选择工具、魔棒工具、对象选择工具

目录 快速选择工具 1、位置 2、3种模式&#xff1a;新选区、添加到选区、从选区减去 3、画笔的设置参数 画笔大小&#xff1a;识别的范围 硬度&#xff1a;边缘的识别能力 间距&#xff1a;识别的连贯程度 跟【选区工具】配套使用的快捷键 1、按【ALT】减区 2、放大…
阅读更多...
数据结构之排序【快速排序和归并排序的非递归代码实现及分析】

数据结构之排序【快速排序和归并排序的非递归代码实现及分析】

引言&#xff1a; 今天因为要写论文&#xff0c;所以现在有点迟了&#xff0c;并且此时是北京时间&#xff1a;2022/12/28/1:41 ,我发现晚睡我真的是专业的&#xff0c;当然睡觉我也是专业的&#xff0c;懂的都懂&#xff0c;现在有点迟加上天大寒&#xff0c;手指不可屈伸&am…
阅读更多...
android之View的滑动

android之View的滑动

其实不管是哪种滑动方式&#xff0c;基本思想都是类似的&#xff1a;当点击事件传递到View时&#xff0c;系统记下触摸点的坐标&#xff0c;手指移动的时候&#xff0c;系统记下移动后的坐标&#xff0c;并计算出偏移量&#xff0c;并通过偏移量来修改View的坐标。 下面我们来…
阅读更多...
黑客比程序员高在哪里？

黑客比程序员高在哪里？

黑客其实和一般的程序员一样&#xff0c;但是他们的关注点不一样。黑客关注的是如何破坏&#xff0c;通过这些有创造性的破坏来获取利益&#xff0c;展现自己的能力。而程序员关注的是如何创造&#xff0c;通过创造来获取利益&#xff0c;展现自己的能力。 就如同一个硬币的两…
阅读更多...
CCF BDCI｜算能赛题决赛选手说明论文-01

CCF BDCI｜算能赛题决赛选手说明论文-01

基于TPU平台实现人群密度估计 加速器队伍 黄显钧 个人名义参赛 中国-广东广州peterhuang0323qq.com 团队简介 加速器队伍队长&#xff1a;黄显钧&#xff0c;现任某科技公司的高级工程师&#xff0c;技术栈涉足嵌入式全栈开发&#xff0c;AI 开发等领域&#xff0c;对技术充满…
阅读更多...
云桌面 Vscode 远程debug python

云桌面 Vscode 远程debug python

云桌面 Vscode 远程debug python1、进入云桌面2、下载VScode配套软件3、挂载本地磁盘4、安装软件4.1 安装VScode4.2 安装插件vsix文件4.3 在服务端安装vscode server5、VScode 配置6、远程调试6.1 python解释器选择6.2 设置debug7. mtu 配置Author: 沧海一阳1、进入云桌面 根据…
阅读更多...
傻白入门芯片设计，盘点计算机体系结构顶会

傻白入门芯片设计，盘点计算机体系结构顶会

目录 一、集成电路/半导体领域的三大顶会&#xff1a; &#xff08;1&#xff09;ISSCC &#xff08;2&#xff09;IEDM &#xff08;3&#xff09;VLSI 二、计算机体系结构四大顶会 &#xff08;1&#xff09;ISCA &#xff08;2&#xff09;HPCA &#xff08;3&#x…
阅读更多...
42. 网络中的网络（NiN）

42. 网络中的网络（NiN）

LeNet、AlexNet和VGG都有一个共同的设计模式&#xff1a;通过一系列的卷积层与汇聚层来提取空间结构特征&#xff1b;然后通过全连接层对特征的表征进行处理。 AlexNet和VGG对LeNet的改进主要在于如何扩大和加深这两个模块。 或者&#xff0c;可以想象在这个过程的早期使用全连…
阅读更多...
利用GithubPage和Hexo搭建个人博客

利用GithubPage和Hexo搭建个人博客

title: 利用Github搭建个人博客 date: 2022-11-28 20:55:30 tags: [blogs] categories: Hexo 建立Git远程仓库 固定格式为&#xff1a;name.github.io ![]](https://img-blog.csdnimg.cn/fa9d7320d1cc422a8a79f2b41dd8458e.png) 开启Github Pages 设置github的token登陆 连接…
阅读更多...
免费在线绘制高颜值，带填充的连贯堆叠柱状图

免费在线绘制高颜值，带填充的连贯堆叠柱状图

堆叠柱状图是我们日常工作中经常使用的一类图形。然而当分类较多时&#xff0c;堆叠柱状图看起来不是那么清晰&#xff0c;通过添加额外的连线&#xff0c;可以增加堆叠柱状图的颜值&#xff0c;给人一种连贯的感觉&#xff0c;并且能够更好地观察数据比例的变化。 图1. 堆叠柱…
阅读更多...
1.8 异常 模块和包

1.8 异常 模块和包

文章目录了解异常异常的捕获方法为什么需要捕获异常捕获常规的异常捕获指定的异常捕获多个异常捕获所有的异常异常else异常的finally异常的传递Python模块模块的导入自定义模块测试模块\_all\_模块Python包了解异常 当我们的解释器运行时发生了一些没办法的操作&#xff0c;或…
阅读更多...
初学Java web(十)

初学Java web(十)

Filter和Listener 一.Filter 概念&#xff1a;Filter表示过滤器&#xff0c;是JavaWeb三大组件(Servlet、Filter、Listener)之一。 过滤器可以把对资源的请求拦截下来&#xff0c;从而实现一些特殊的功能。 过滤器一般完成一些通用的操作&#xff0c;比如&#xff1a;权限控…
阅读更多...
新键盘到了，我的工作效率提升了数十倍

新键盘到了，我的工作效率提升了数十倍

前言&#xff1a;快过年了&#xff0c;找到了一份满意的实习&#xff0c;正好旧的键盘坏掉了&#xff0c;最近入手了一款不错的机械键盘奖励自己。到货使用一段时间了&#xff0c;来一篇键盘开箱的博客做一个反馈。 新键盘使用感言&#xff1a;优良的键盘如图云上漫步&#xf…
阅读更多...
白质中的BOLD信号激活检测问题

白质中的BOLD信号激活检测问题

白质中BOLD信号的生理意义存在争议的两个主要原因&#xff1a; BOLD信号依赖于脑血流量CBF和脑血容量CBV&#xff0c;但是白质中的血流量和血容量比灰质中的少得多&#xff08;利用MRI估计的微血管数量&#xff1a;白质为10-192条/mm^2&#xff0c;灰质为99-761条/mm^2&#x…
阅读更多...
【GUI界面】基于Python的WSG84三点定位系统（经纬度坐标与平面坐标转换法求解）

【GUI界面】基于Python的WSG84三点定位系统（经纬度坐标与平面坐标转换法求解）

【GUI界面】基于Python的WSG84三点定位系统&#xff08;经纬度坐标与平面坐标转换法求解&#xff09; 方法汇总&#xff1a; blog.csdn.net/weixin_53403301/article/details/128441789 【精准三点定位求解汇总】利用Python或JavaScript高德地图开放平台实现精准三点定位&…
阅读更多...
[开源工具]使用Fiddler简单计算QPS[新手开箱可用]

[开源工具]使用Fiddler简单计算QPS[新手开箱可用]

使用Fiddler简单计算QPS1.什么是QPS?2.怎么计算QPS?3.如何使用Fiddler得到一个API接口的QPS?3.1配置&#xff1a;打开Fiddler文件夹&#xff0c;点击Fiddler.exe运行fiddler进行配置4.如何得到本机的核心数?5.根据公式计算QPS?6.扩展计算单机可支撑PV(理论值)?1.什么是QP…
阅读更多...
springboot中controller层接收参数，servers层调用mapper层，一条sql搞定排序

springboot中controller层接收参数，servers层调用mapper层，一条sql搞定排序

前言 很多小伙伴们在公司不管是测试C端产品还是B端产品&#xff0c;都会测到排序的业务需求&#xff1b;那么我们就会好奇排序是如何实现的呢&#xff1f;下面我们开始介绍代码的实现 数据库建表 我们需要创建一个书籍book表结构&#xff0c;如下图所示 CREATE TABLE book ( …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023