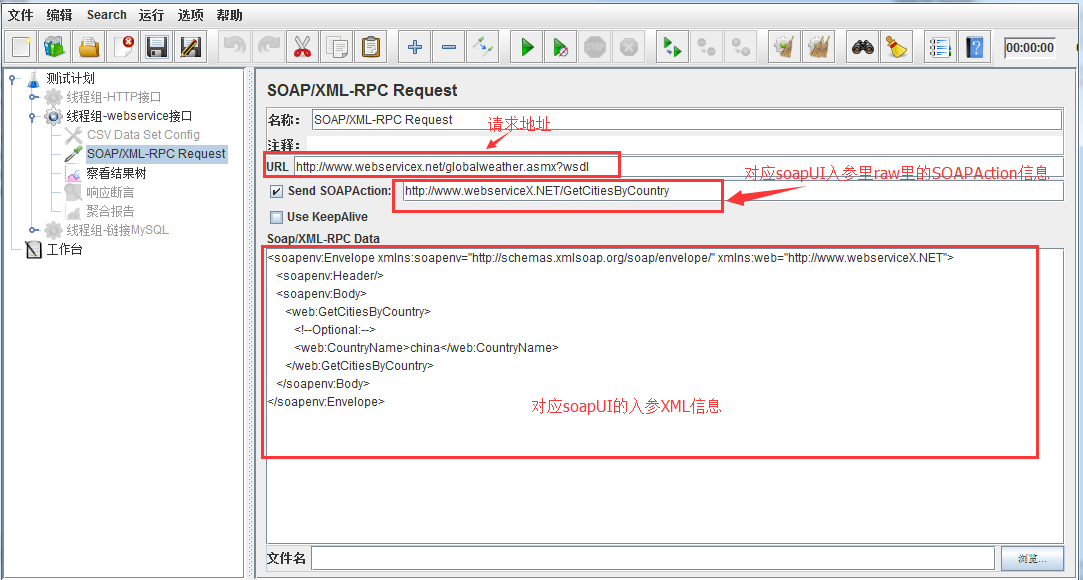
今天的内容是C盘清理系列的第二期——盘符划分操作。
1. 点击“我的电脑——左上角的管理”
2.进入后点击磁盘管理
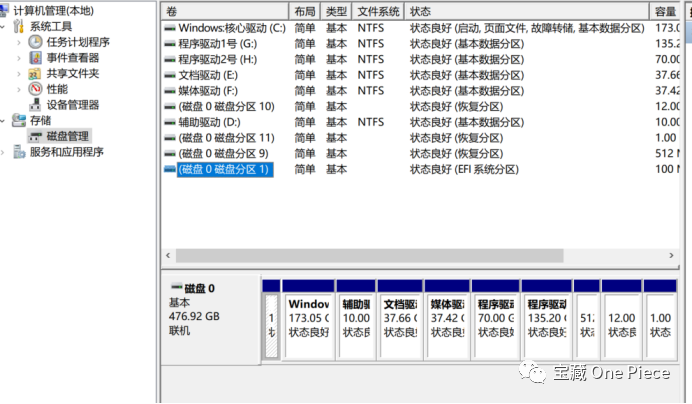
3.右键单击某个想修改盘符,可进行扩展、压缩、删除三种操作
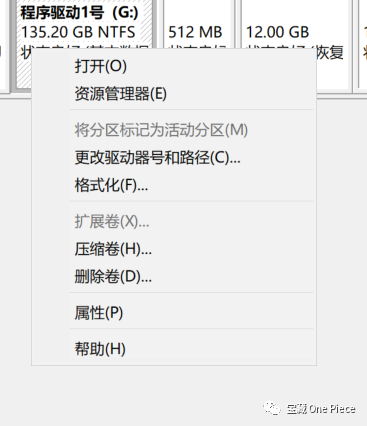
其中压缩卷是进行“分解反应”,即原盘过大要进行拆分。此处注意拆分的上限为“总空间-已用空间”,当压缩空间大于拆分上限时,系统会提示错误。所以大家一定要算清楚自己需要的存储空间哦(计算机内存进制为2的十次方,即1024,相信大家都会算,这里不过多赘述)。
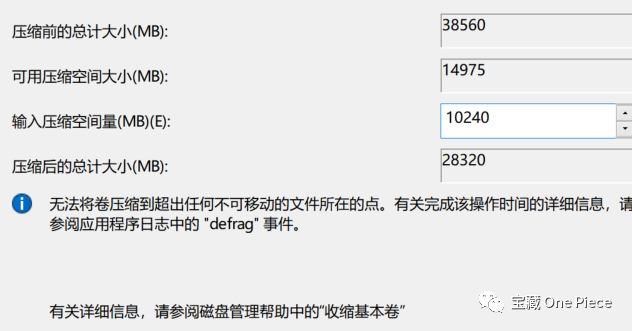
而扩展卷则是将系统中未利用的空白卷添加到你想添加的盘符,这里由于学长的电脑里面已经全部分配完毕了,第四步学长会展示压缩与扩展的进一步操作。
而删除卷大家可一定要看清楚再点哦,删除卷相当于格式化磁盘,说白了就是释放全部内存空间,如果操作不慎磁盘里面的原有文件也会一起凉凉哦。
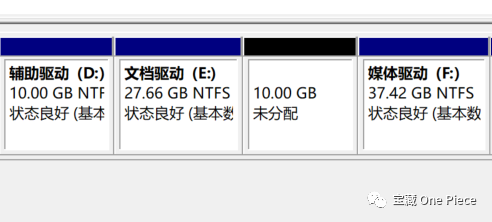
4.大家注意,如上是学长对E盘进行了压缩卷后的效果,原有37G内存的E盘被拆分成了27+10G,其中27是真正的E盘,而10G则成为了压缩后的空白卷。
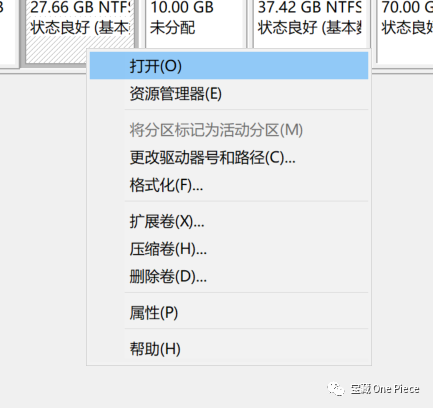
如图所示,右键单击E盘,发现E盘此时可扩展,这是因为E盘之后有空白卷10G,故可将其加入划分出来的C盘。
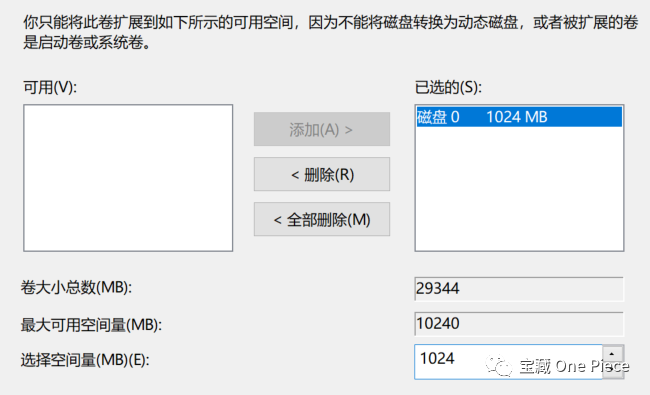
右键单击进入后选择想要分配的大小,这里为了后续演示,学长先加入了一个G。
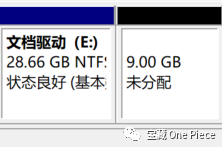
结果如图。
5.重难点
这时就会有小伙伴们提出,那如果我想把空白卷加入D盘或者F盘可以吗?我们不妨用刚才剩余的9G来做个试验。
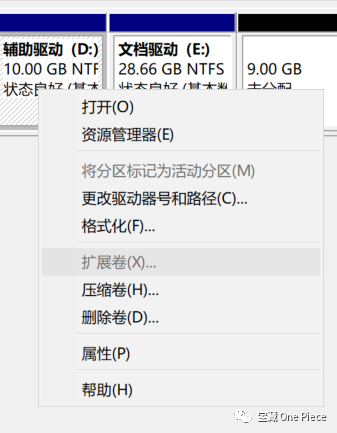
然而我们会发现,无论是D盘还是F盘,在我们点击扩展卷部分时,该选项变为灰色,意为无法实现!
为什么会发生这样的事情呢,难道分出来的扩展卷只能原路返回母体吗?不妨我们再做个试验2来试一下。
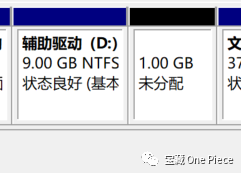
如图所示,学长将D盘分出来1G后,仍然无法向其他盘符扩容,综上所述,难道只能给自己恢复分区的理论是成立的吗?
码农一向追求严谨性,为了证实结论,接下来请看实验3:
学长将D盘内的文件转移后,决定对D盘使用删除卷的操作!
前方高能!!!

漂亮(归曼牺牲得好惨bushi)

这时我们发现,之前一直不能进行扩容的C盘居然奇迹般地可以扩容了!
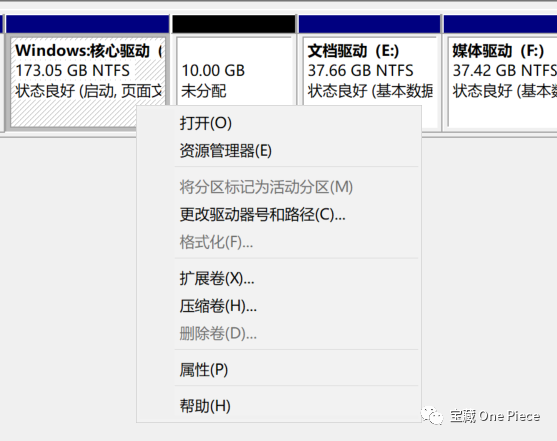
当然,学长这里只是做个试验,现在给C盘扩容duck不必,还是复活归曼要紧。
这里附加一个创建新分区的教学哦:
右键单击空白卷,显示新建简单卷。
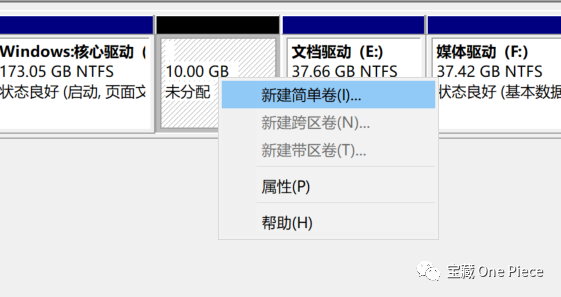
点击后进行分盘(这里可以选择分配的驱动型号)
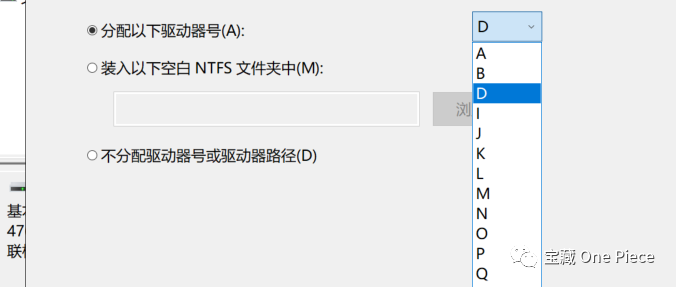
之后就一直默认就好了。
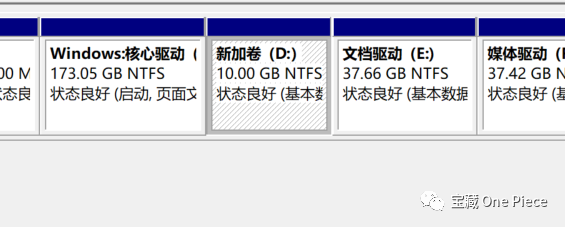
大功告成,归曼复活!

相信上述3个试验,大家一定总结出来了规律:要想给盘符扩容,必须保证此盘符右边紧挨着空白卷,如果旁边没有直接挨着的空白卷,则无法实现扩容。

那为什么会出现这种排序方式呢,这种方式能进行更改吗?
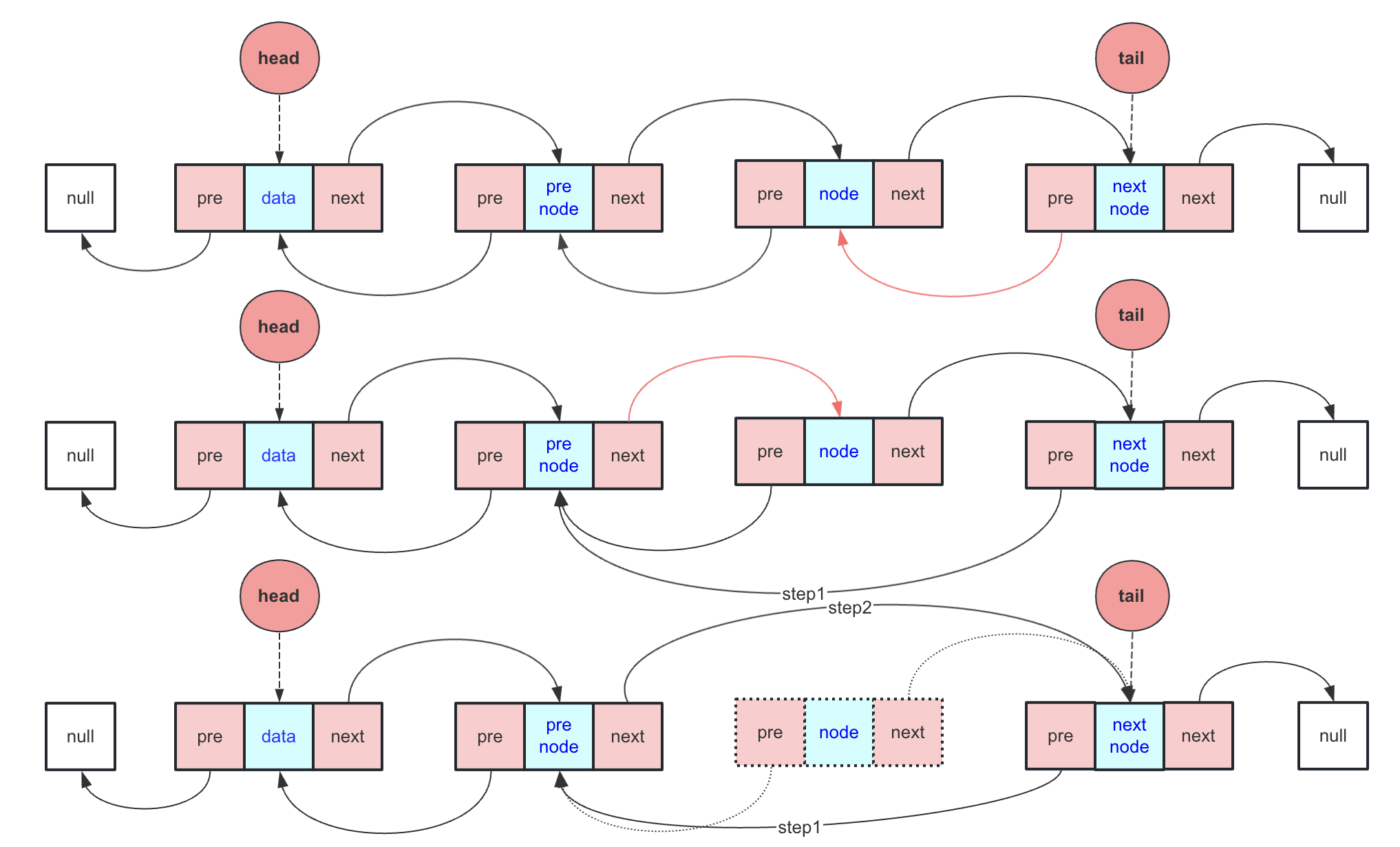
很遗憾,先天的畸形在后期治愈时会非常麻烦。这里学长做了两个流程图,来给大家展示盘符诞生的两种思路:
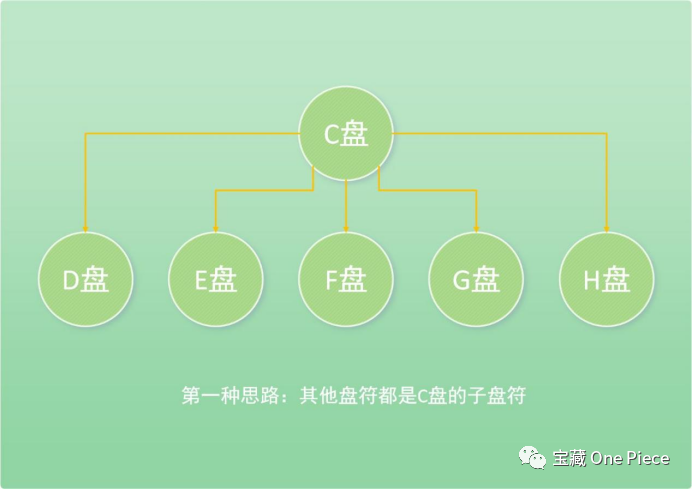
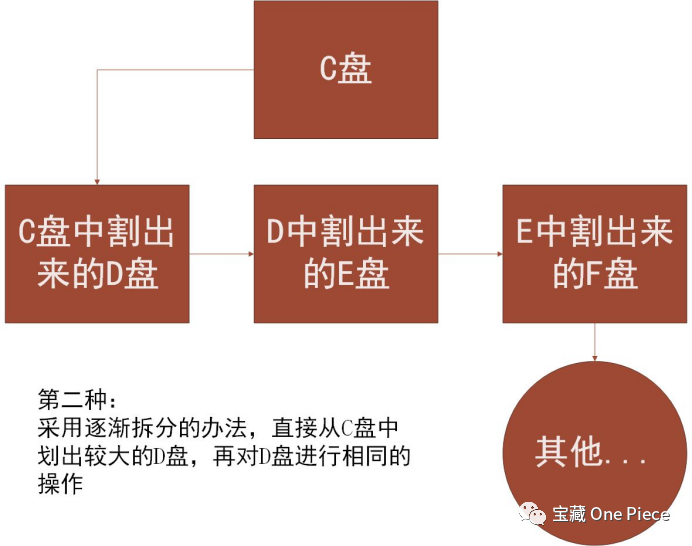
学长在这里做出一个假设,只有从当前盘符直接划分出去的空间在变为空白卷后才能合并回去!
现在,学长打算用F盘分出来5G的空间,来作为本源的模拟C盘(C1),进行实验四对上述两种办法进行证明。
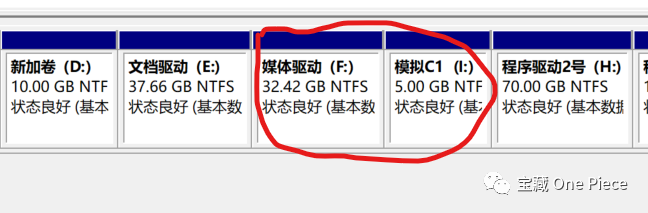
如图所示,建立模拟C盘
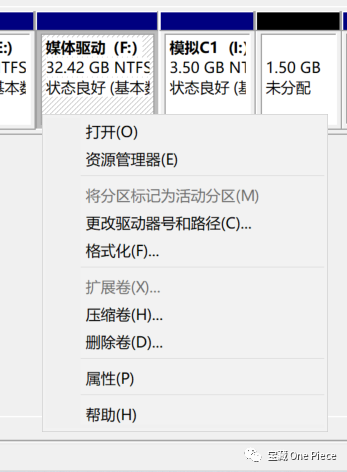
如图,学长从模拟C1中分出了1.5G的空白卷,能向上兼容回C1盘符中,却不能补回到F盘中,证明了第二种逐级递减的划分方式中,只能直接返回上一级,而不能跳级。当然,这时只要删除卷C1,即可将5G全部兼容进F盘。
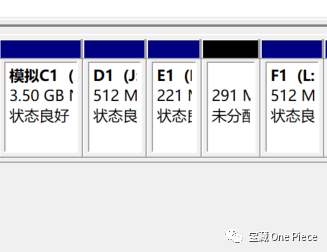
进一步分区,此处采用第一种方式,直接将1.5G空白采用均分划分,再将F1子盘砍半,新的空白卷同样无法兼容到母体的母体C1,或者母体的兄弟D1,E1中。

经过一番折腾,学长的电脑已经面目全非了,不过学长已经是久病成良医了,这点玩机技巧还是很容易复原的,大家如果对自己电脑的结构没有清晰的认识的话,千万不要频繁分盘哦!这对电脑和内存都是不小的伤害。
说来说去,解决最上面为何不能兼容的问题,这里再简单的总结一下:
空白卷只能返回直接母体,而不是自由更改去向。
学长的电脑之所以不能从F盘中挖一部分送给G盘,原因就是学长采用了第一种方式——全部的盘符都是从C盘直接划分的。那大家又会问,那F盘划出来的空间为什么不能回归C盘呢?哈哈,后面我们不是证明了么,只返回直接母体,此时C盘的子盘是F盘,而不是F盘中划出来新的子盘。如果想回归C盘,那么8好意思,只能删除卷F盘,再一起回归咯。
这里学长已经进行了简单的复原。啊,其实还是挺麻烦的,这辈子能远离尽量远离计算机。

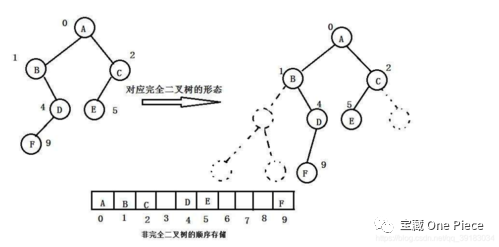
其实部分专业的同学如果学过《数据结构》这门课,就会发现盘符划分的两种方式与树和线性表很类似。为了方便后期更改,建议大家采用第二种逐级递减的方式进行,因为这样可以向上合并。而如果用第一种,大家都在同一级,就比较麻烦了。
不过,大家最好在买来新电脑的第一时刻就改好分区,且不要随便更改,因为移动文件路径的话,真的会带来不小的麻烦。另外,还是学长说的,适度分盘,并且c盘里面不要放重要文件,之后学长会进一步讲解其他的原因哦。今天就讲到这里。