【调度算法】并行机调度问题遗传算法

问题描述

m台相同的机器，n个工件，每个工件有1道工序，可按照任意的工序为每个工件分配一台机器进行加工

工件	A	B	C	D	E	F	G	H	I
工件编号	0	1	2	3	4	5	6	7	8
加工时间	4	7	6	5	8	3	5	5	10
到达时间	3	2	4	5	3	2	1	8	6
交货期	10	15	30	24	14	13	20	18	10

设备数目：3

目标函数

最小化交货期总延时时间

编码说明

记机器数为m，从0开始编号为0,1,...,m-1，记工件数为n，同样从0开始编号。

定义两个变量job_id和job，前者表示工件的加工顺序（不是严格意义上的先加工A再加工B这种顺序，这里的每个工件都是独立的，整一个id只是为了再分配完机器之后自然就能选出一种加工顺序），后者表示每个工件用哪台机器加工。

例如，job_id=[4, 0, 5, 8, 1, 6, 2, 7, 3]，job=[0, 1, 2, 2, 1, 0, 2, 1, 0]表示“编号为4的工件被分配给了编号为0的机器”，“编号为0的工件被分配给了编号为1的机器”，编号为0的机器上工件加工的先后顺序为4,6,3，其余类推。

注意，并行机调度问题里边对于染色体的编码一般分为机器选择部分和工件排序部分，机器选择部分，就是正常这里应该是先给工件分配机器，再对每台工件上分配的机器进行排序，但是我这个代码里就是先直接对工件进行乱序然后再选择机器，乍一听好像最后的效果差不多，但是看代码就会知道，我代码里是对job_id进行乱序之后，直接就一种群为单位进行选择交叉变异了。即，一个job_id值对应一个种群（而非一个个体，但是理论上应该是每个个体对对饮过一个不同的顺序），就可能会导致处理大规模问题的时候时间复杂度太高（这里确实是偷懒了但是我这两天看代码真的看麻了5555，菜是原罪），有能力的好兄弟改好了可以踢我一下。

具体思路可以看这篇：https://blog.csdn.net/qq_38361726/article/details/120669250

运算结果

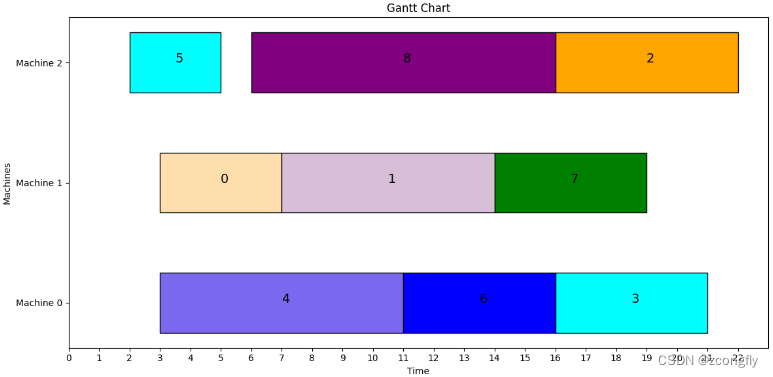
最佳加工顺序： [4, 0, 5, 8, 1, 6, 2, 7, 3]
最佳调度分配： [0, 1, 2, 2, 1, 0, 2, 1, 0]
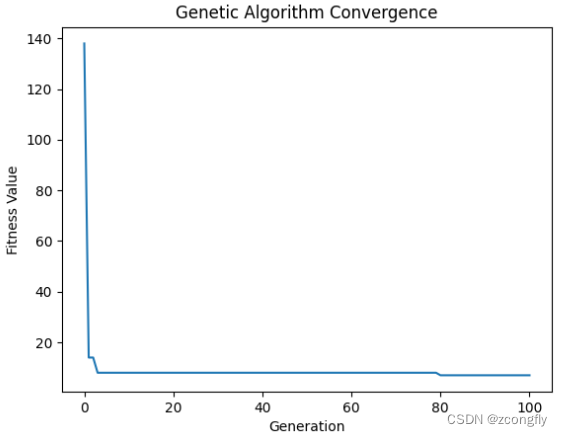
最小交货期延时时间： 7

在这里插入图片描述

python代码

import random
import numpy as np
import matplotlib.pyplot as plt
import copy


# 定义遗传算法参数
POP_SIZE = 100  # 种群大小
MAX_GEN = 100  # 最大迭代次数
CROSSOVER_RATE = 0.7  # 交叉概率
MUTATION_RATE = 0.2  # 变异概率


def sort_by_id(id, sequence):
    # 根据id对sequence进行排序
    new_sequence = sequence[:]
    for i in range(len(id)):
        sequence[i] = new_sequence[id[i]]


# 随机生成初始种群，这里的每个个体表示第i个工件选择在第choose[i]台机器进行加工，工件和机器编码都是从0开始
def get_init_pop(pop_size):
    pop = []
    for _ in range(pop_size):
        choose = []
        for _ in range(len(job_id)):
            choose.append(random.randint(0, machine_num - 1))
        pop.append(list(choose))
    return pop


# 计算染色体的适应度（makespan） 以最小化交货期延时为目标函数，这里计算的是交货期总延时时间
def fitness(job):
    delay_times = [[] for _ in range(machine_num)]  # 每个工件超过交货期的延时时间
    finish_times = [[] for _ in range(machine_num)]  # 每个工件完成加工的时间点
    for i in range(len(job)):
        if finish_times[job[i]]:
            finish_times[job[i]].append(
                pro_times[job_id[i]] + max(finish_times[job[i]][-1], arr_times[job_id[i]]))
        else:
            finish_times[job[i]].append(pro_times[job_id[i]] + arr_times[job_id[i]])
        delay_times[job[i]].append(max(finish_times[job[i]][-1] - deadlines[job_id[i]], 0))

    return sum(element for sublist in delay_times for element in sublist)


# 选择父代，这里选择POP_SIZE/2个作为父代
def selection(pop):
    fitness_values = [1 / fitness(job) for job in pop]  # 以最小化交货期总延时为目标函数，这里把最小化问题转变为最大化问题
    total_fitness = sum(fitness_values)
    prob = [fitness_value / total_fitness for fitness_value in fitness_values]  # 轮盘赌，这里是每个适应度值被选中的概率
    # 按概率分布prob从区间[0,len(pop))中随机抽取size个元素，不允许重复抽取，即轮盘赌选择
    selected_indices = np.random.choice(len(pop), size=POP_SIZE // 2, p=prob, replace=False)
    return [pop[i] for i in selected_indices]


# 交叉操作 这里是单点交叉
def crossover(job_p1, job_p2):
    cross_point = random.randint(1, len(job_p1) - 1)
    job_c1 = job_p1[:cross_point] + job_p2[cross_point:]
    job_c2 = job_p2[:cross_point] + job_p1[cross_point:]
    return job_c1, job_c2


# 变异操作
def mutation(job):
    index = random.randint(0, len(job) - 1)
    job[index] = random.randint(0, machine_num - 1)  # 这样的话变异概率可以设置得大一点，因为实际的变异概率是MUTATION_RATE*(machine_num-1)/machine_num
    return job


# 主遗传算法循环
# 以最小化延迟交货时间为目标函数
# TODO: 没有考虑各机器的负载均衡
def GA(is_shuffle):  # 工件加工顺序是否为无序
    best_id = job_id  # 初始化job_id
    best_job = [0, 0, 0, 0, 0, 0, 0, 0, 0]  # 获得最佳个体
    # "makespan" 是指完成整个生产作业或生产订单所需的总时间，通常以单位时间（例如小时或分钟）来衡量。
    best_makespan = fitness(best_job)  # 获得最佳个体的适应度值
    # 创建一个空列表来存储每代的适应度值
    fitness_history = [best_makespan]

    pop = get_init_pop(POP_SIZE)
    for _ in range(1, MAX_GEN + 1):
        if is_shuffle:
            random.shuffle(job_id)
        pop = selection(pop)  # 选择
        new_population = []

        while len(new_population) < POP_SIZE:
            parent1, parent2 = random.sample(pop, 2)  # 不重复抽样2个
            if random.random() < CROSSOVER_RATE:
                child1, child2 = crossover(parent1, parent2)  # 交叉
                new_population.extend([child1, child2])
            else:
                new_population.extend([parent1, parent2])

        pop = [mutation(job) if random.random() < MUTATION_RATE else job for job in new_population]
        best_gen_job = min(pop, key=lambda x: fitness(x))
        best_gen_makespan = fitness(best_gen_job)  # 每一次迭代获得最佳个体的适应度值

        if best_gen_makespan < best_makespan:  # 更新最小fitness值
            best_makespan = best_gen_makespan
            best_job = copy.deepcopy(best_gen_job)  # TODO: 不用deepcopy的话不会迭代，但是这里应该有更好的方法
            best_id = copy.deepcopy(job_id)
        fitness_history.append(best_makespan)  # 把本次迭代结果保存到fitness_history中（用于绘迭代曲线）

    # 绘制迭代曲线图
    plt.plot(range(MAX_GEN + 1), fitness_history)
    plt.xlabel('Generation')
    plt.ylabel('Fitness Value')
    plt.title('Genetic Algorithm Convergence')
    plt.show()

    return best_id, best_job, best_makespan


def plot_gantt(job_id, job):
    # 准备一系列颜色
    colors = ['blue', 'yellow', 'orange', 'green', 'palegoldenrod', 'purple', 'pink', 'Thistle', 'Magenta', 'SlateBlue',
              'RoyalBlue', 'Cyan', 'Aqua', 'floralwhite', 'ghostwhite', 'goldenrod', 'mediumslateblue', 'navajowhite',
              'moccasin', 'white', 'navy', 'sandybrown', 'moccasin']
    job_colors = random.sample(colors, len(job))
    # 计算每个工件的开始时间和结束时间
    start_time = [[] for _ in range(machine_num)]
    end_time = [[] for _ in range(machine_num)]
    id = [[] for _ in range(machine_num)]
    job_color = [[] for _ in range(machine_num)]

    for i in range(len(job)):
        if start_time[job[i]]:
            start_time[job[i]].append(max(end_time[job[i]][-1], arr_times[job_id[i]]))
            end_time[job[i]].append(start_time[job[i]][-1] + pro_times[job_id[i]])
        else:
            start_time[job[i]].append(arr_times[job_id[i]])
            end_time[job[i]].append(start_time[job[i]][-1] + pro_times[job_id[i]])
        id[job[i]].append(job_id[i])
        job_color[job[i]].append(job_colors[job_id[i]])

    # 创建图表和子图
    plt.figure(figsize=(12, 6))

    # 绘制工序的甘特图
    for i in range(len(start_time)):
        for j in range(len(start_time[i])):
            plt.barh(i, end_time[i][j] - start_time[i][j], height=0.5, left=start_time[i][j], color=job_color[i][j],
                     edgecolor='black')
            plt.text(x=(start_time[i][j] + end_time[i][j]) / 2, y=i, s=id[i][j], fontsize=14)

    # 设置纵坐标轴刻度为机器编号
    machines = [f'Machine {i}' for i in range(len(start_time))]
    plt.yticks(range(len(machines)), machines)

    # 设置横坐标轴刻度为时间
    # start = min([min(row) for row in start_time])
    start = 0
    end = max([max(row) for row in end_time])
    plt.xticks(range(start, end + 1))
    plt.xlabel('Time')

    # 图表样式设置
    plt.ylabel('Machines')
    plt.title('Gantt Chart')
    # plt.grid(axis='x')

    # 自动调整图表布局
    plt.tight_layout()

    # 显示图表
    plt.show()


if __name__ == '__main__':
    # 定义多机调度问题的工件和加工时间
    job_id =    [0, 1, 2, 3, 4, 5, 6, 7, 8]  # 工件编号
    pro_times = [4, 7, 6, 5, 8, 3, 5, 5, 10]  # 加工时间
    arr_times = [3, 2, 4, 5, 3, 2, 1, 8, 6]  # 到达时间
    deadlines = [10, 15, 30, 24, 14, 13, 20, 18, 10]  # 交货期
    machine_num = 3  # 3台完全相同的并行机，编号为0,1,2

    job_id, best_job, best_makespan = GA(True)

    print("最佳加工顺序：", job_id)
    print("最佳调度分配：", best_job)
    print("最小交货期延时时间：", best_makespan)
    plot_gantt(job_id, best_job)