文章目录
- 一、什么是机器学习?
- 二、什么时候可以使用机器学习?
- 三、感知机perceptron
- 四、机器学习的输入形式
- 五、机器真的可以学习吗?
- 六、vc dimension
一、什么是机器学习?
其实第一个问题和第二个问题是穿插到一块儿回答的,首先机器学习要解决的是常规的if-else类编程无法解决的问题,也就是说我们的if-else无法涵盖到所有的情况(即,输入程序的数据分布是不可知的)。
有如下问题:
- 给定一个有向图的邻接矩阵,判断该有向图是不是DAG,该问题不需要使用机器学习求解,因为我们已经知道了DAG的定义,即我们有了输入数据的分布,根据定义就可以进行判断;
- 给定一张照片,判断照片中有没有包含一只猫,该问题不能使用常规编程进行解决,因为我们不知道一只猫的精确定义是什么,我们也没有这个世界上所有包含猫的照片(输入数据分布不可知),此时我们需要让机器学习一些判定是否包含猫的一些技能,需要使用机器学习求解该问题。
机器学习正式的定义如下图所示:
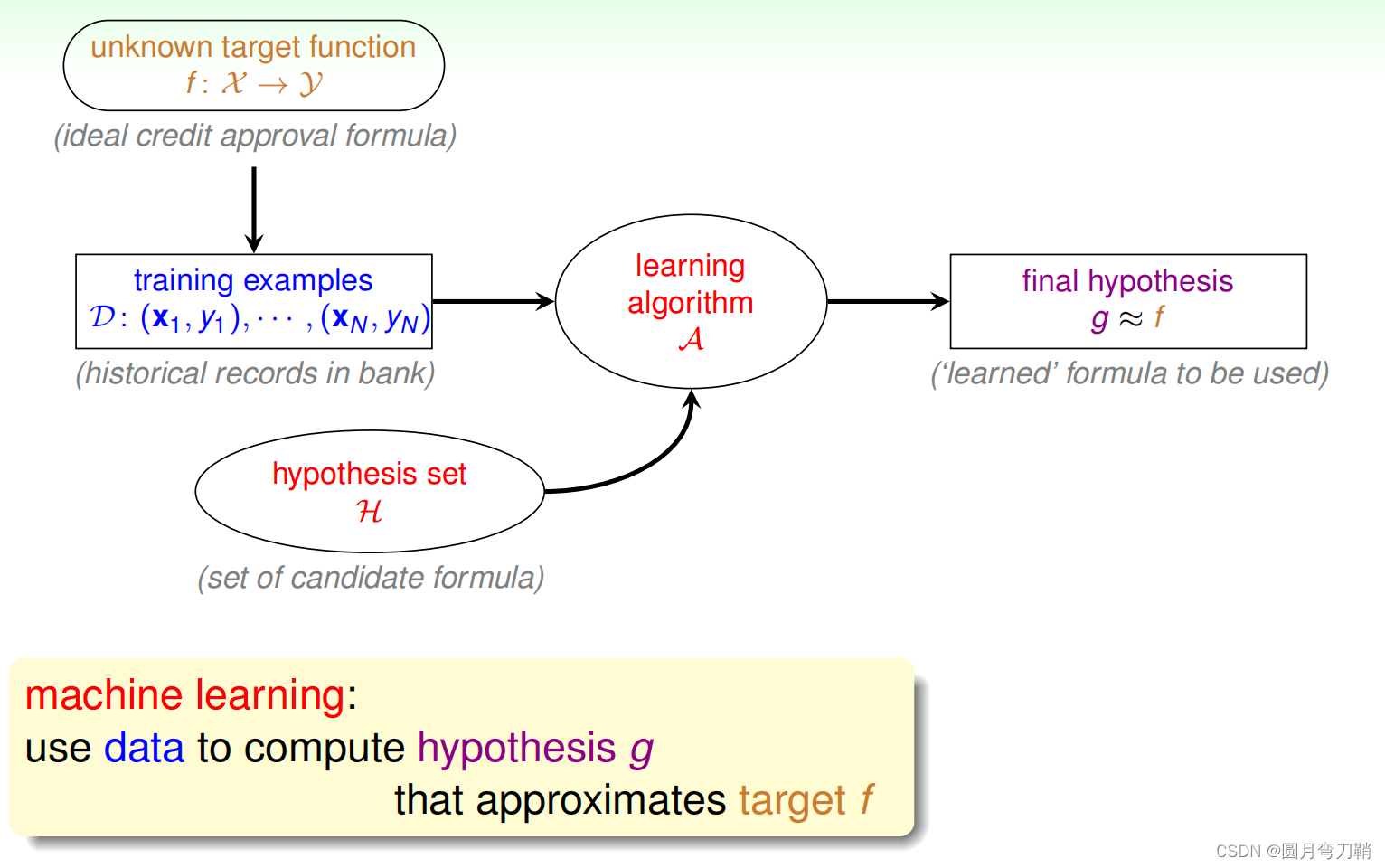
首先我们的目标是要寻找一个函数
f
f
f(目标函数target function),将我们的输入放入
f
f
f中,我们预期可以得到不错的输出,世界中的函数千千万,如何寻找这个函数
f
f
f是个难题。
我们现在手上有的只是一堆数据
D
D
D,这些数据是应用规则
f
f
f产生的(或许还会加上一些noise)。为了尽可能的减小我们寻找
f
f
f的难度,我们假设了一些可能会比较接近
f
f
f的函数集合叫做hypothesis set,使用设计好的算法
A
A
A和数据集
D
D
D,从hypothesis set中找到与我们预期最相符的函数
g
g
g,将它近似的当作
f
f
f。通常将hypothesis set和算法
A
A
A加到一块儿叫做模型,也有直接将hypothesis set叫做模型的。
所以机器学习的任务就是大海捞针,在哪片海捞由我们自己决定,怎么捞由我们自己决定,捞出来的针是不是我们想要的针,我们也不知道,只不过有霍夫丁不等式可以保证我们捞出来的针在概率上是我们想要的针。
二、什么时候可以使用机器学习?
第一个问题已经回答了when to use ML。
三、感知机perceptron
感知机是一个回答yes or no的线性二分类模型,是最简单的机器学习模型。感知机的任务目标是给定一堆数据,将这些数据正确的分割开的,感知机的hypothesis set中就是一堆线性的超平面。我们需要从中选择一个可以将现有数据分割开的平面。
感知机学习算法(perceptron learning algorithm/PLA)使用的策略是知错能改,首先随机初始化一个线性超平面,选择一个分类错误的点,让我们分类超平面以如下形式去调整:
w
(
t
+
1
)
=
w
t
+
y
n
x
n
w_{(t+1)}=w_t+y_nx_n
w(t+1)=wt+ynxn
如此循环往复,直到所有点都分类正确。
对于线性可分的数据,最终我们是可以得到一个不错的分类超平面的,但是由于我们是随机选择错误分类的点,所以最终我们能得到的分类超平面是不唯一的。
关于感知机的另外一个版本见此感知机另外一种解释。
四、机器学习的输入形式
机器学习的输入无非就是特定长度的向量,每个样本用一个若干维的向量表示,只是这些向量以及每一维有没有明确的意义呢,答案是肯定的。
我们是为了将我们的输入进行数字化,才使用向量来表示输入的,因为要让机器可以处理,就必须是数字。
我们可以为向量的每一维赋予明确的意义,比如,描述一个人,就可以用性别,年龄,身高,体重,学历等一系列和任务相关的特征,将这些特征表示成数字的形式,比如,性别用0/1,年龄用正整数,身高用实数。像这种有明确意义的特征叫做concrete feature。
机器学习任务多种多样,输入也不尽相同,有些输入无法给每一维赋予明确的解释,比如图像处理任务,通常都是用像素点的RGB值来作为特征,这叫做raw feature,当然同样的输入,可以表示成raw feature或concrete feature,合理即可,比如,minist手写数字识别的输入,可以用像素点表示,也可以通过定义数字的对称与否,高矮胖瘦来描述样本。
总之,言之成理的feature都可以用来描述样本,在这一点上feature的使用是比较灵活的。
五、机器真的可以学习吗?
机器学习是从已知的数据中学习规则,应用到未知的数据上,对未知数据进行判断。
既然如此,机器学习就是在做不可能的事情,因为我们不可能准确无误的掌握所有的数据,也就是说学习到的规则总有偏差。当不能对一件事一窥全貌的时候,就需要用到概率工具了。
假如有一个装了无数个黑白球的罐子,我们想知道其中白球的比例,但是又不可能知道罐子中总共有多少个黑球白球。一个看似合理的方法是,我们从罐子中取出来
N
N
N个球(我们可以数得清的一批球),数清楚这批球,计算这批球中白球的比例,似乎可以用这个比例代替真实的比例。有Hoeffding Inequality作为保证,
P
(
∣
比
例
观察
−
比
例
真实
∣
<
ϵ
)
≥
2
e
x
p
(
−
2
ϵ
2
N
)
P(|比例_{观察}-比例_{真实}|\lt\epsilon)\geq 2exp(-2\epsilon^2N)
P(∣比例观察−比例真实∣<ϵ)≥2exp(−2ϵ2N)
当
N
N
N足够大,
ϵ
\epsilon
ϵ也合适的时候我们说观察到的比例等于真实的比例,这种说法大概是正确的(Probably Approximately Correct / PAC)。
霍夫丁不等式告诉我们的是,面对一个数据量非常大,大到我们无法精确进行处理的时候,我们可以从这个大数据中进行多次i.i.d.采样,这样我们采样得到的数据集在一定程度上代表了那个原始的大数据。只要采样数据足够,关于大数据的各项特性,我们都可以通过采样数据进行估计。
将以上过程类比到机器学习,关于某个任务的所有数据被分成了两部分,一部分是我们已经有的训练数据,另一部分是我们无法获得的数据,我们现在从hypothesis set中找到了一个函数,在训练数据上获得了良好的表现,我们怎么确保这个函数在无法的验证的数据上也同样表现良好呢?Hoeffding Inequality comes to rescue。
所以只要霍夫丁不等式得到了满足,我们就只需要关注我们手上有的数据就行了,让这部分数据在模型上获得良好的表现即可。
总结一下:
假设
E
i
n
E_{in}
Ein是训练数据的表现误差,
E
o
u
t
E_{out}
Eout是得不到的数据的表现误差,一个良好的机器学习模型,需要做到:
- E i n E_{in} Ein足够小 (我们自己训练,并且模型的能力足够)
-
E
i
n
≈
E
o
u
t
E_{in} \approx E_{out}
Ein≈Eout(Hoeffding Inequality得到保证)
从另一种角度来说,通常通过合适的算法和迭代训练,我们可以将
E
i
n
E_{in}
Ein做的比较小,即训练数据上的模型表现不错,但是能否保证
E
o
u
t
E_{out}
Eout也是这样的一个根本影响因素是,我们的训练数据是否具有代表性,即能否和整体数据保持分布一致或相近,比如,整体数据是黑球白球各1000个,做数据集大小为10的采样,很不幸,我刚好采样到一个数据集中10个球全是白球,这样的几率虽然相对较小,但是也是会发生的。这个采样毫无疑问是一个Bad data。
给定很多采样数据集和hypothesis set,有下表,
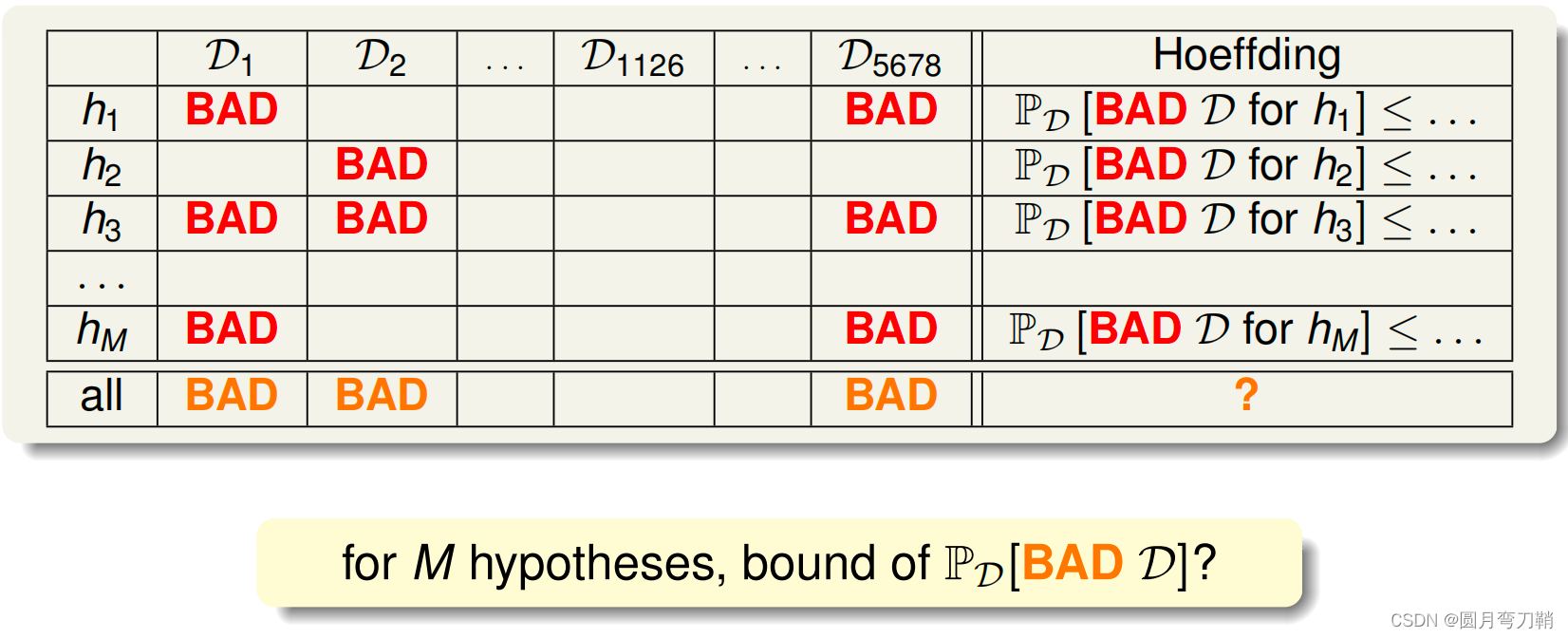
利用霍夫丁不等式进行推导如下:

由上述推导可得,如果
M
M
M是有限的,并且
N
N
N足够大,我们就能保证我们手上的不是Bad data,即
E
i
n
E_{in}
Ein和
E
o
u
t
E_{out}
Eout比较接近。
接着上面推导结果中的
M
M
M和
N
N
N,
N
N
N没什么好说的,越大越好,但是
M
M
M呢,它代表hypothesis set中备选函数的数量,如果
M
M
M太小,Bad data的概率虽然变小了,但是备选空间也小了,我们可能选不到很合适的函数,如果
M
M
M太大,备选空间是足够大了,Bad data的概率就变大了。我们需要一个合适大小的
M
M
M,再来看Bad data概率的推导公式,union bound的地方把所有项加起来有点粗暴,因为hypothesis set中两个备选函数之间是有可能有交集的,这样子的话最终
M
M
M也许并没有想象中那么大。
考虑感知机分类的情形,我们的hypothesis set中虽然看似包含了无数个线性超平面,但是实际有效的超平面个数是有限的,当有1个点要分类的时候,有效超平面只有两个,要么将这个点判断为正,要么判断为负,有2个点,3个点,4个点的情形也类似,如下图所示:
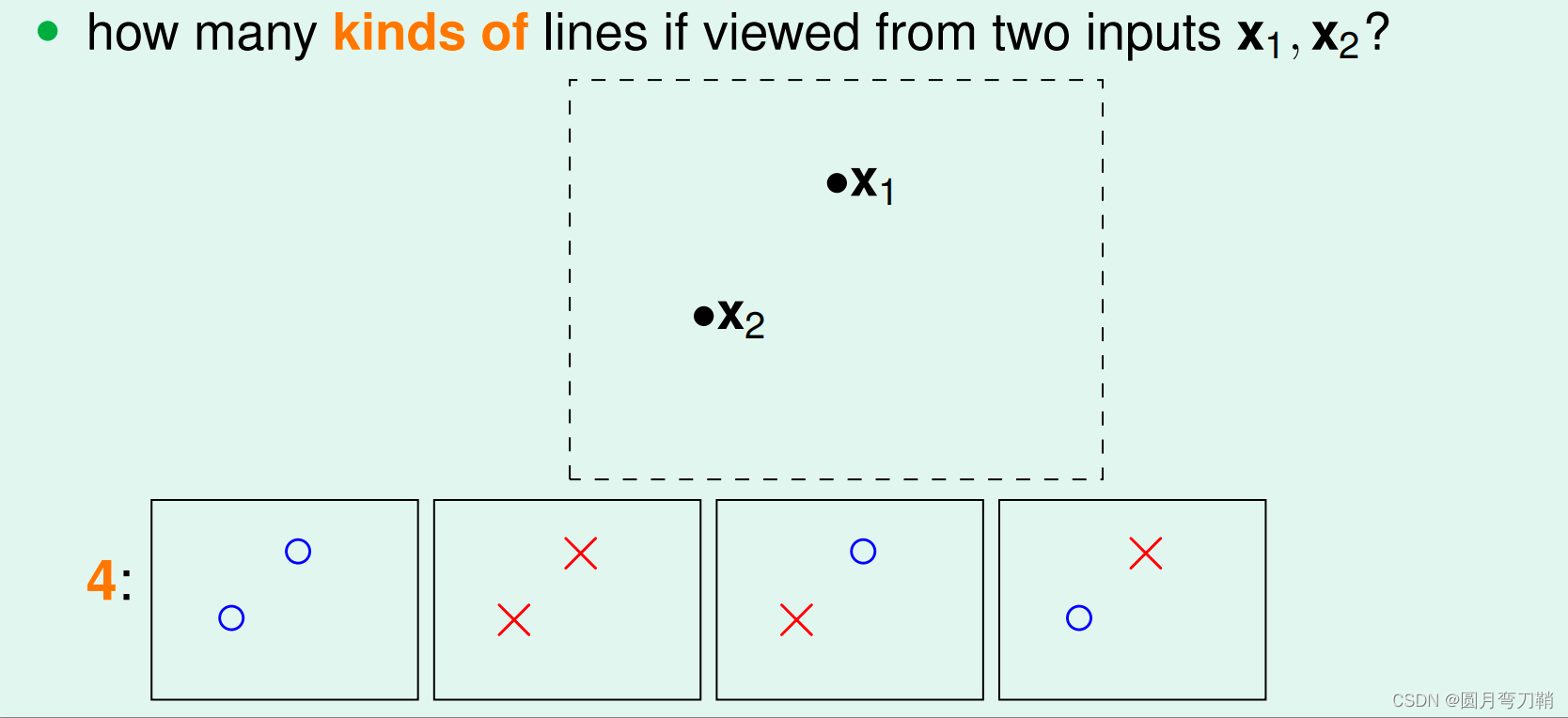
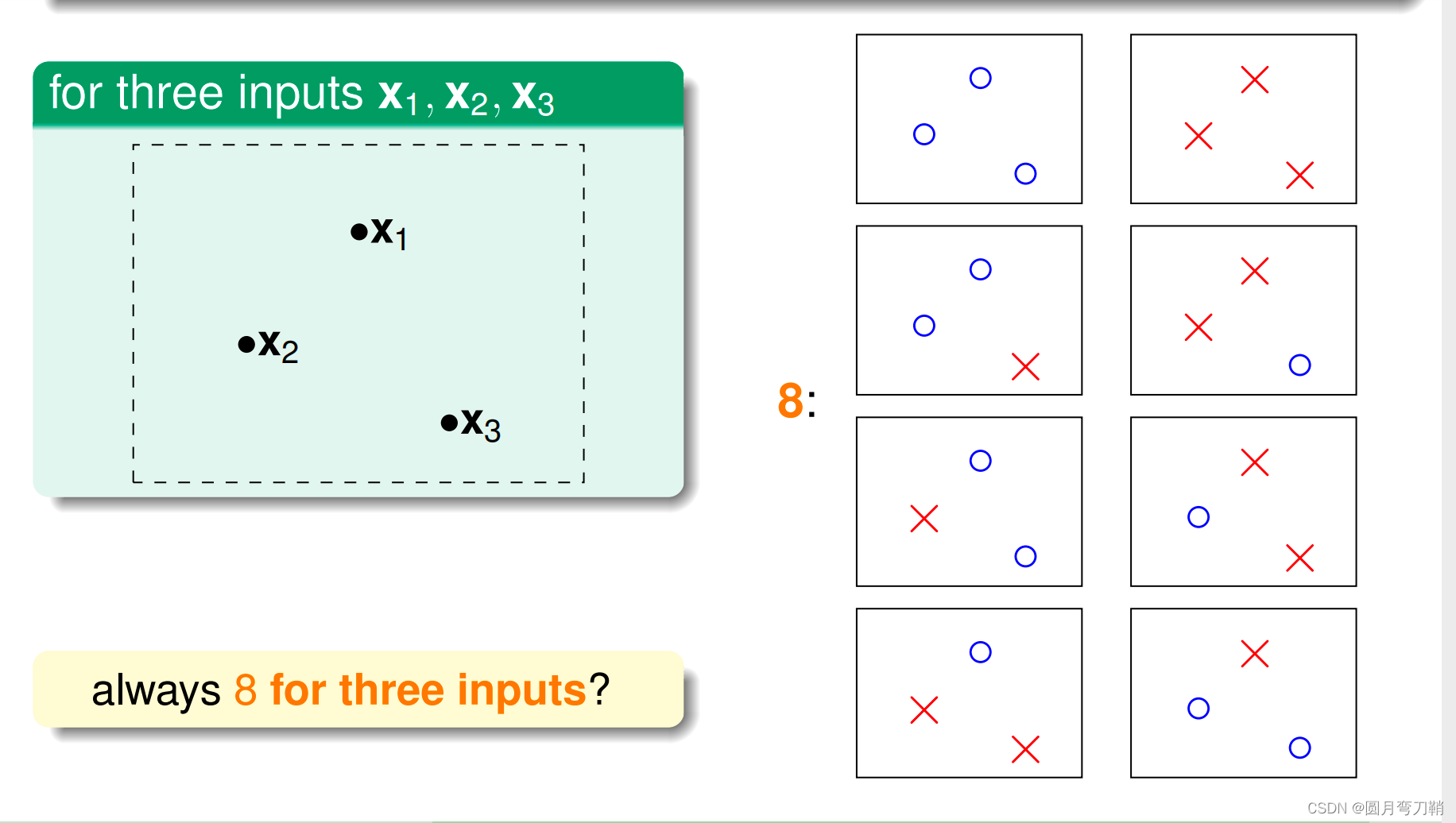
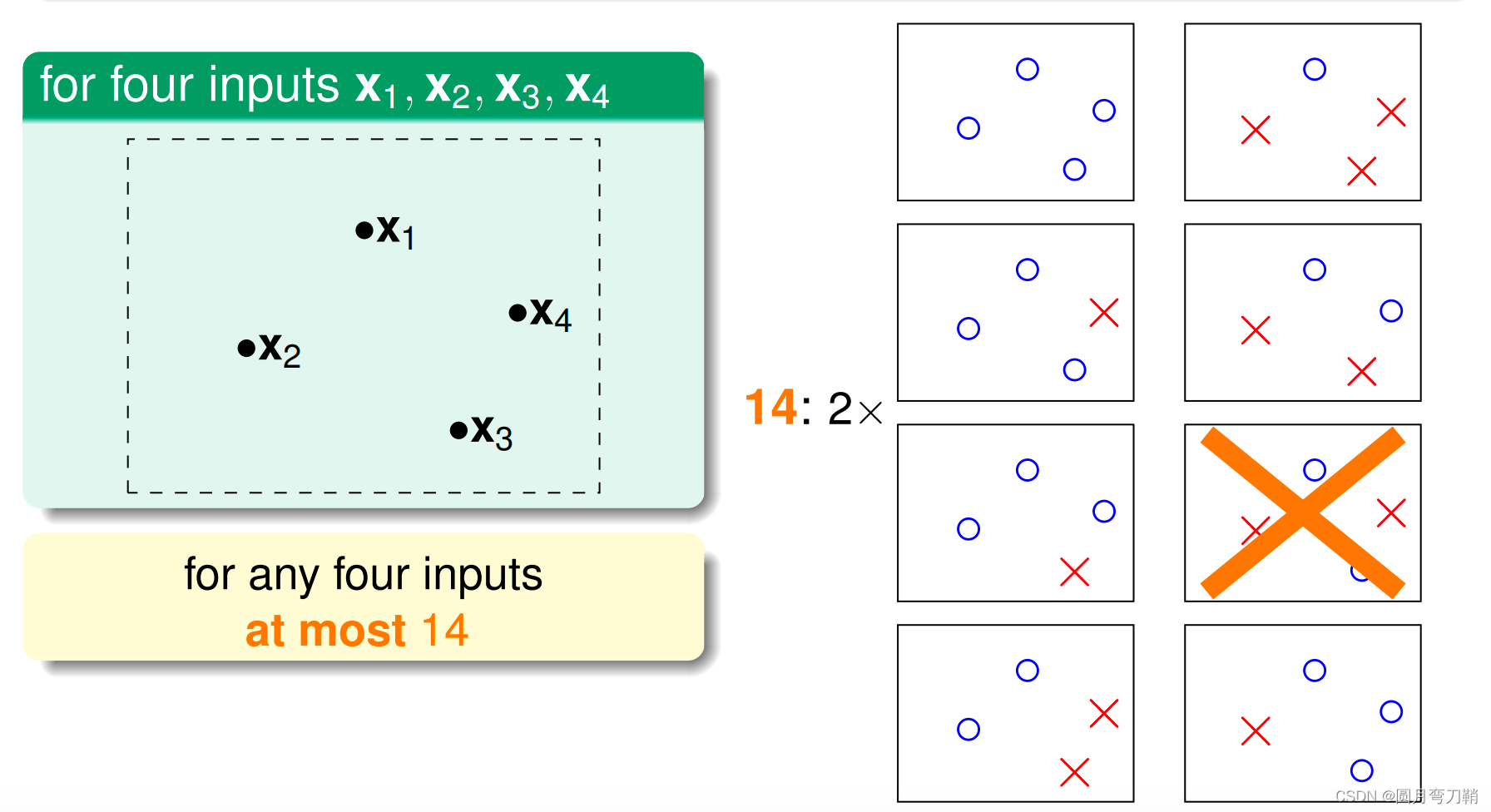
情况似乎有所明朗,在4个点的情况中,有效超平面的个数已经小于
2
4
2^4
24了(4这个点被称为break point)。
M
M
M似乎可以得到简化,既然如此,针对不同的hypothesis set,不同的数据集大小(即不同的任务,不同的模型),我们是否可以找到一个上限,而且是多项式上限,而非指数级别的上限,答案是肯定的,这样的上限是存在的,证明过程见林轩田老师的机器学习基石。
如此一来,只要我们的hypothesis set存在break point,并且数据集足够大,
E
i
n
E_{in}
Ein和
E
o
u
t
E_{out}
Eout很接近就可以在概率上得到保证。最后有公式如下:
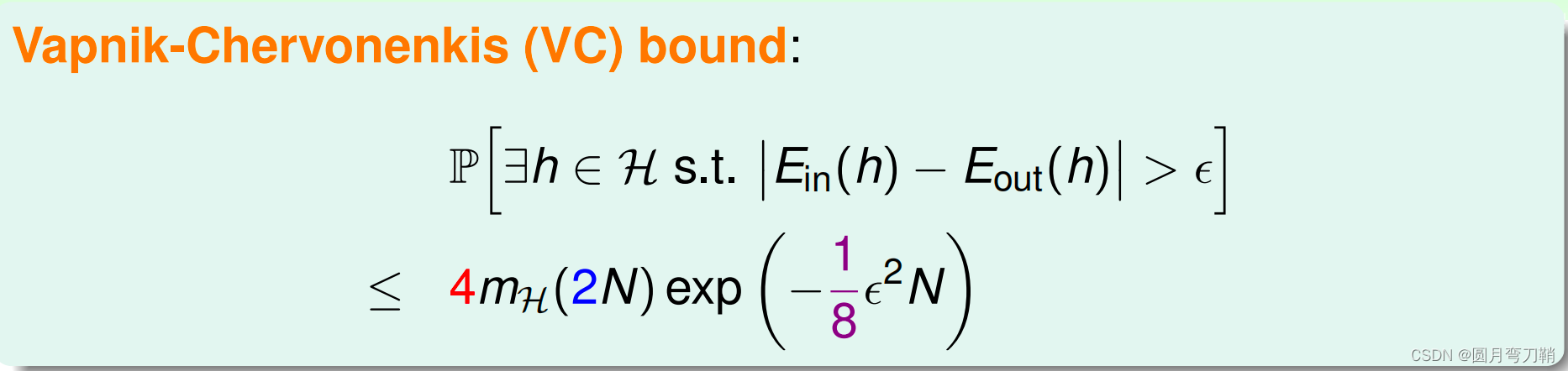
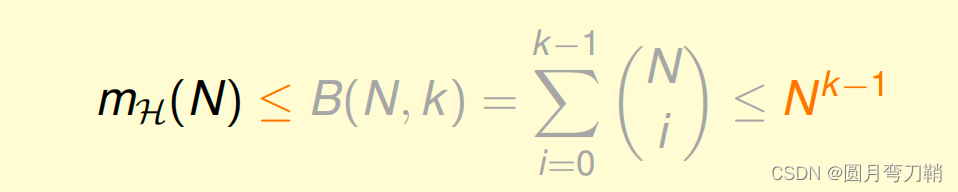
六、vc dimension
上文中提到,“在4个点的情况中,有效超平面的个数已经小于
2
4
2^4
24了”,这里的4被称为break point,而vc dimension就是break point-1,对于上面的情形来说就是3,但是我们关于vc dimension的说明并不是计算,而是希望理解vc dimension的含义。
在二元分类的情况下,vc dimension等于hypothesis set的参数数量,比如2维感知机,有3个参数(包含2个权重决定分割线的斜率和1个截距)。vc dimension是hypothesis set能力或者自由度的一种指标,vc dimension越大,说明hypothesis set中包含了更广泛的函数,以致于我们可以在这个很大的hypothesis set中找到我们想要的函数(在训练数据上表现好的函数)。
我们在上面的表述都是在说坏事情(
E
i
n
E_{in}
Ein和
E
o
u
t
E_{out}
Eout相隔很大)发生的概率,我们尝试找到一个多项式的上限约束坏事情发生的概率。现在我们看霍夫丁不等式的一个变形:
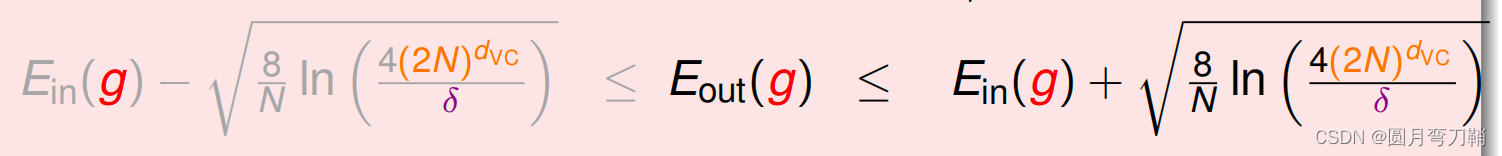
可以看到,影响
E
i
n
E_{in}
Ein和
E
o
u
t
E_{out}
Eout之间差距的因素很多,有
N
N
N,vc dimension,
δ
\delta
δ,我们现在看vc dimension对公式的影响,vc dimension越大,模型能力越强,
E
i
n
E_{in}
Ein会更小,但是后面那个复杂的一项也会同时变大,会有如下一个常见的趋势:

即,vc dimension并不是越大(模型能力越强)越好,模型能力太强会过拟合。
再来看数据集大小
N
N
N对
E
i
n
E_{in}
Ein和
E
o
u
t
E_{out}
Eout之间差距的影响,直觉上数据量肯定越多越好,但是实际过程中,可靠数据的取得是很困难的,所以理论上为了保证机器学习的可靠性,所需的数据量和vc dimension有如下关系:
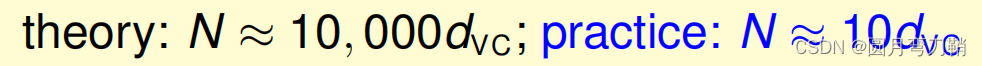
之所以theory和practice之间有如此大的差距,是因为我们上面推导的不等式上限是很宽松的,它涵盖了各种hypothesis set,各种数据集大小,各种机器学习算法,各种目标函数。