分类目录：《深入理解强化学习》总目录

因为对动作—价值的估计总会存在不确定性，所以试探是必须的。贪心动作虽然在当前时刻看起来最好，但实际上其他一些动作可能从长远看更好。$ϵ-$贪心算法会尝试选择非贪心的动作，但是这是一种盲目的选择，因为它不大会去选择接近贪心或者不确定性特别大的动作。在非贪心动作中，最好是根据它们的潜力来选择可能事实上是最优的动作，这就要考虑到它们的估计有多接近最大值，以及这些估计的不确定性。一个有效的方法是按照以下公式选择动作：
$$A_t=\arg \underset{a}{\max }[Q_t(a)+c\sqrt{\frac{\ln t}{N_t(a)}}]$$

在这个公式里，$\ln t$表示的自然对数，$N_t(a)$表示在$t$时刻之前动作$a$被选择的次数。$c$是一个大于0的数，它控制试探的程度。如果$N_t(a)=0$，则$a$就被认为是满足最大化条件的动作。

这种基于置信度上界（UpperConfidence Bound，UCB）的动作选择的思想是，平方根项是对$a$动作值估计的不确定性或方差的度量。因此，最大值的大小是动作$a$的可能真实值的上限，参数$c$决定了置信水平。每次选$a$时，不确定性可能会减小；由于$N_t(a)$出现在不确定项的分母上，因此随着$N_t(a)$的增加，这一项就减小了。另一方面，每次选择$a$之外的动作时，在分子上的增大，而$N_t(a)$却没有变化，所以不确定性增加了。自然对数的使用意味着随着时间的推移，增加会变得越来越小，但它是无限的。所有动作最终都将被选中，但是随着时间的流逝，具有较低价值估计的动作或者已经被选择了更多次的动作被选择的频率较低。

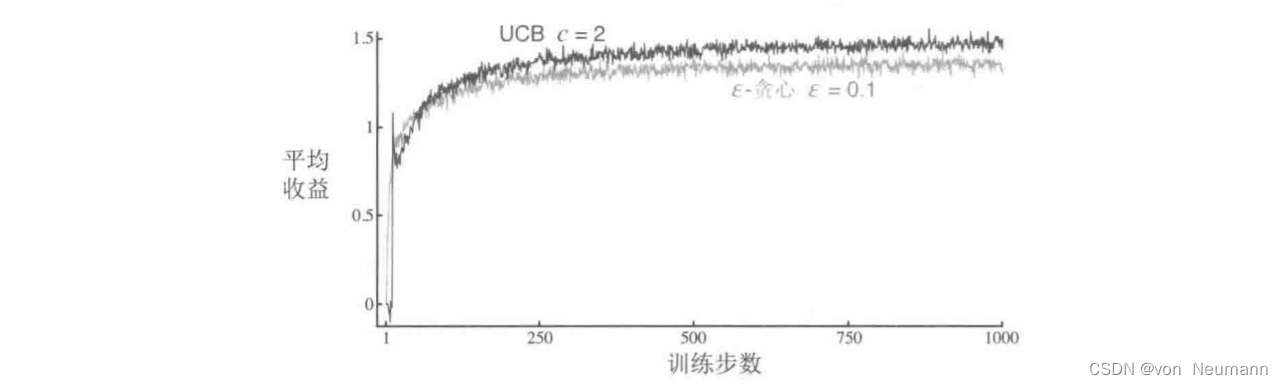
下图展示了在10臂测试平台上采用UCB算法的结果。如图所示，UCB往往会表现良好。但是和$ϵ-$贪心算法相比，它更难推广到其它一些更一般的强化学习问题。一个难题是要处理大的状态空间，目前还没有已知的实用方法利用UCB动作选择的思想。

参考文献：
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习（第2版）[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践（原书第2版）[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL：强化学习教程 [M]. 人民邮电出版社, 2022