QuantLib学习笔记——一个简单的价值估算案例

news2024/12/24 1:05:31

⭐️ 前言

QuantLib很强大，它实现了很多金融工具及其价值估算方法，从最简单的折现模型，到利用BSM模型对期权进行定价，覆盖面相当齐全。本文以一个简单的净现值估算案例，开启笔者金融工具估值的旅程。
在这里插入图片描述
开上豪车，出发！！！

⭐️ 一些概念

这里介绍一些金融投资上的概念，以便我们顺利进行接下来的实验。

名称	解释
Portfolio	投资组合，其中包含多个相同或不同的金融工具，例如可以包含一个期权和一个现金存款，也可以包含一个固定利率现金流和一个浮动利率现金流
Leg	投资组合中的每一种金融工具，例如上面的期权，或者现金存款，或者现金流
Cashflow	现金流，即一次现金的流入流出，主要属性包括日期及现金金额
Coupon	票息，即债券持有人每次获得的利息，他也是一种现金流

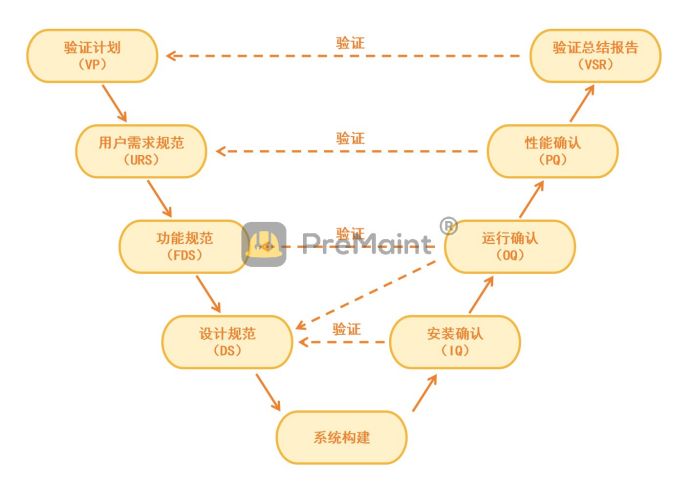
他们的关系如下图

在这里插入图片描述

⭐️ 实验债券

债券的概念，这里就不细说了，点进来的小伙伴们应该都很熟悉了，我们讨论这样一种附息债券，债券持有人会在债券到期前，每隔一段时间获得一次票息，债券到期时，会获得最后一次利息和票面金额，具体来说，票面金额为100元，每次票息为5元，每隔一年支付一次票息，有效期4年。

⭐️ NPV

NPV，就是净现值，它是将未来的现金流按折现率或利率折合成现在的值，然后将折合后的所有现值相加得到的。本文也会给出折现率和NPV的关系。
在这里插入图片描述

本文的实验就是计算上面描述的债券的NPV。

⭐️ 观察者模式

观察者模式是程序设计当中常用的设计模式，当被观察者发生改变时，会将这种改变通知所有观察者，观察者们会根据具体的情况执行相应的操作。
在这里插入图片描述

在QuantLib中，Quote可以将数值包装成被观察者，其他对象例如Term Structures可以注册为该Quote的观察者，当Quote包装的对象改变时，Term Structures会得到通知，重新进行一些计算任务。

⭐️ 代码

import QuantLib as ql
import matplotlib.pyplot as plt


if __name__ == "__main__":
    # 参考日期
    ref_date = ql.Date(1,11,2023)
    # 利率Quote
    rate = ql.SimpleQuote(0.01)
    rate_handle=ql.QuoteHandle(rate)
    # 平直的利率曲线
    curve = ql.FlatForward(ref_date, rate_handle, ql.Actual365Fixed(), ql.Compounded)
    # 利率结构
    yts = ql.YieldTermStructureHandle(curve)    
    # 构造现金流及leg
    cf1 = ql.SimpleCashFlow(5, ref_date + 365)
    cf2 = ql.SimpleCashFlow(5, ref_date + 365*2)
    cf3 = ql.SimpleCashFlow(5, ref_date + 365*3)
    cf4 = ql.SimpleCashFlow(105, ref_date + 365*4)
    leg = ql.Leg([cf1, cf2, cf3, cf4])
    # 面值
    f = 100
    # 票息
    a = 5
    # 绘图坐标值
    x_ = []
    y_ = []
    # 构建绘图数据
    for i in range(5):
        # 修改利率的值
        rate.setValue(rate.value() + 0.01 * i)
        # 利率
        r = round(rate.value(), 2)
        # leg净现值
        npv = ql.CashFlows.npv(leg, yts, True, ref_date)
        
        print("***************************************")
        print(f'利率水平：{r}')
        
        pv=a/(1+rate.value()) + a/(1+rate.value())**2 + a/(1+rate.value())**3 + (a+f)/(1+rate.value())**4
        print(f'直接用折现公式计算的债券价格为：{pv}')
        
        print(f'Quantlib计算的债券价格为：{pv}')
        # 绘图坐标值
        x_.append(r)
        y_.append(npv) 
        
    plt.plot(x_, y_)
    plt.show()

输出结果如下

***************************************
利率水平：0.02
直接用折现公式计算的债券价格为：111.42318609602287
Quantlib计算的债券价格为：111.42318609602287
***************************************
利率水平：0.03
直接用折现公式计算的债券价格为：107.43419680562073
Quantlib计算的债券价格为：107.43419680562073
***************************************
利率水平：0.04
直接用折现公式计算的债券价格为：103.62989522425684
Quantlib计算的债券价格为：103.62989522425684
***************************************
利率水平：0.05
直接用折现公式计算的债券价格为：99.99999999999999
Quantlib计算的债券价格为：99.99999999999999
***************************************
利率水平：0.06
直接用折现公式计算的债券价格为：96.53489438730033
Quantlib计算的债券价格为：96.53489438730033

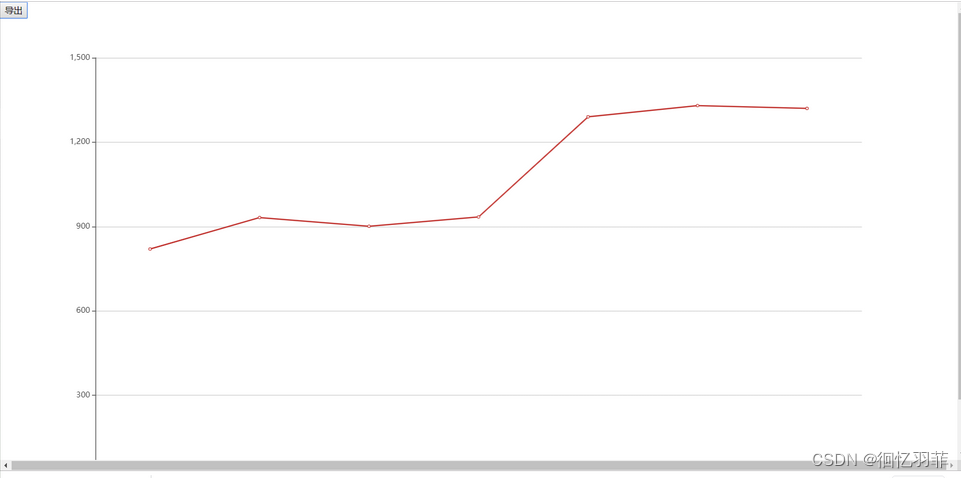
绘图结果如下
在这里插入图片描述
可见，折现率或利率越大，npv则越小。