84.柱状图中最大的矩形

题目：给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。


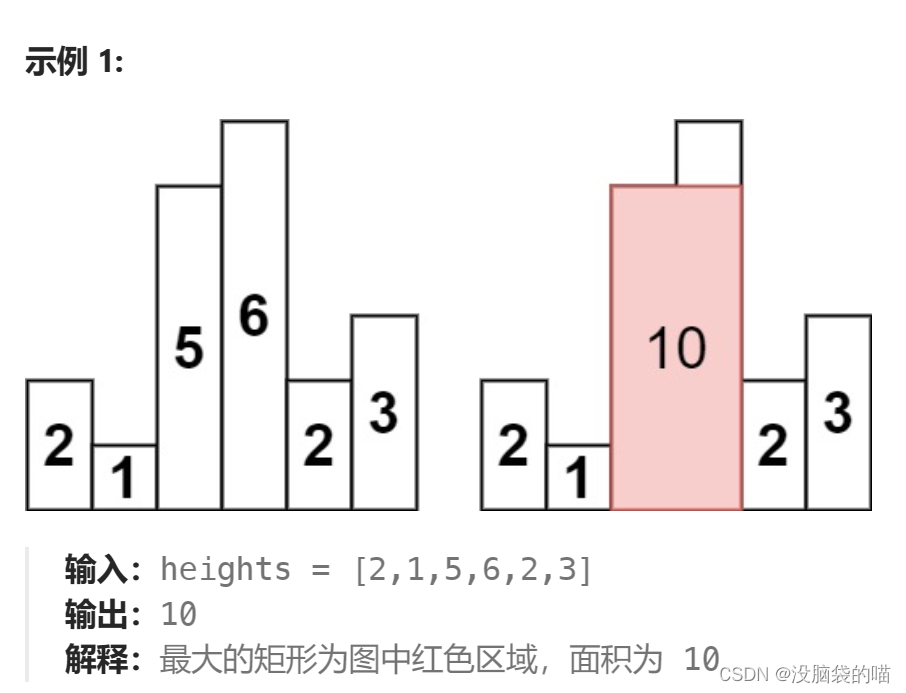
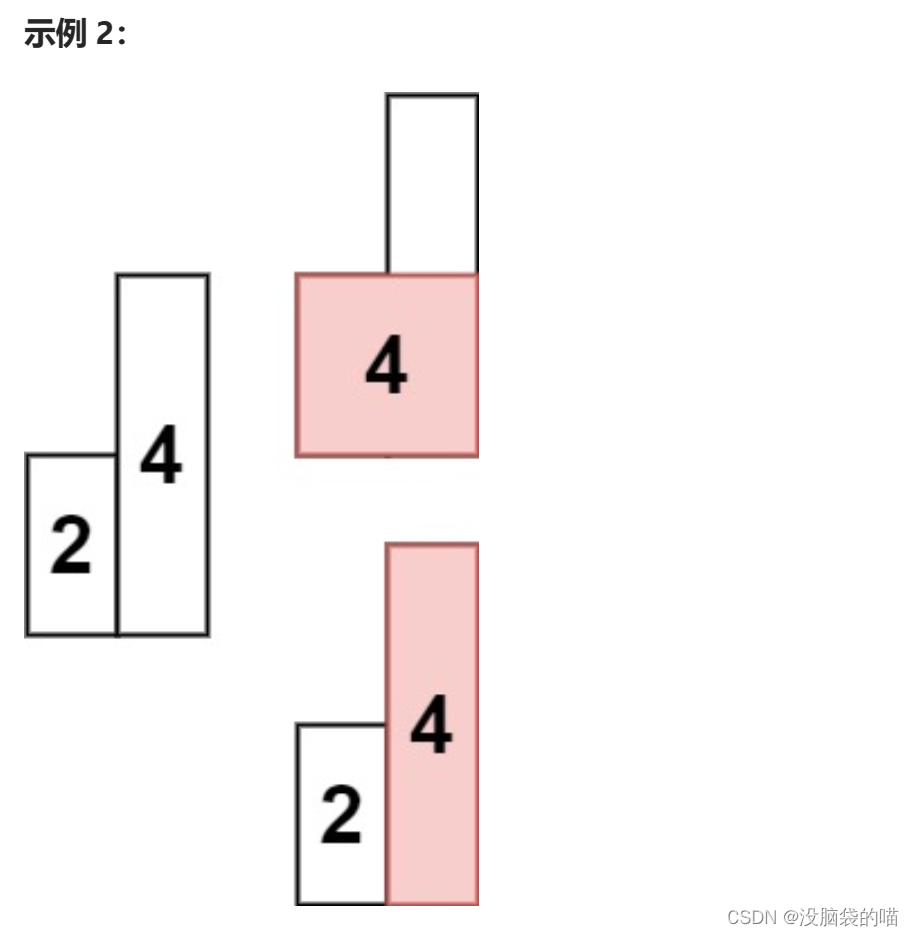
提示：

1 <= heights.length <=105
0 <= heights[i] <= 104

题目链接：84.柱状图中最大的矩形

//单调栈
class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        Stack<Integer> stack=new Stack<Integer>();
        int ans=0;
        //要找左边右边第一个比当前柱子小的元素
        //维护单调递增栈
        //求左边第一个 栈中的是左侧元素 弹出比它大的 栈顶就是比它小的第一个元素
        int[] left=new int[heights.length];
        int[] right=new int[heights.length];
        stack.push(0);
        left[0]=-1;
        for(int i=1;i<heights.length;i++){
            while(!stack.isEmpty()&&heights[i]<=heights[stack.peek()]){
               stack.pop();
            }
            if(stack.isEmpty()){
                left[i]=-1;
            }else{
                left[i]=stack.peek();
            }
            stack.push(i);
        }
        stack.clear();
        for (int i = n - 1; i >= 0; --i) {
            while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
                stack.pop();
            }
            right[i] = (stack.isEmpty() ? n : stack.peek());
            stack.push(i);
        }
        

        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
    //单调栈优化
    //维护一个递增的栈 当入站元素小于栈顶元素时 栈顶元素左边第一个比他小的和右边第一个比它小的都找齐了 直接计算面积即可
    public int largestRectangleArea(int[] heights) {
        int[] newheights = new int[heights.length + 1];
        System.arraycopy(heights,0,newheights,0,heights.length);
        newheights[newheights.length-1]=0;
        int n = newheights.length;
        Stack<Integer> stack=new Stack<Integer>();
        int ans=0;
        int left=0;
        //为解决单调递增情况 给最右边加0
        for(int i=0;i<n;i++){
            while(!stack.isEmpty()&&newheights[i]<newheights[stack.peek()]){
                int mid=newheights[stack.peek()];
                stack.pop();
                if(!stack.isEmpty()){
                   left=stack.peek(); 

                }else{
                    left=-1;
                }
                
                ans=Math.max(ans,(i-left-1)*mid);
            }
            stack.push(i);
        }
        return ans;
    }
}