50. Pow(x, n) - 力扣（LeetCode）

计算 x 的 n 次幂，如果是直接暴力求解的话，会造成计算时间周期过长，所以要从别的角度出发，将幂等数分为两个幂等数相乘，例如：三的八次方，等于三的四次方乘以三的四次方，大致可以分为以下两种情况：

1. 无法分为两个幂等数，则再乘一次 x；

2. 可以分为两个幂等数，即转换为两个幂等数相乘；

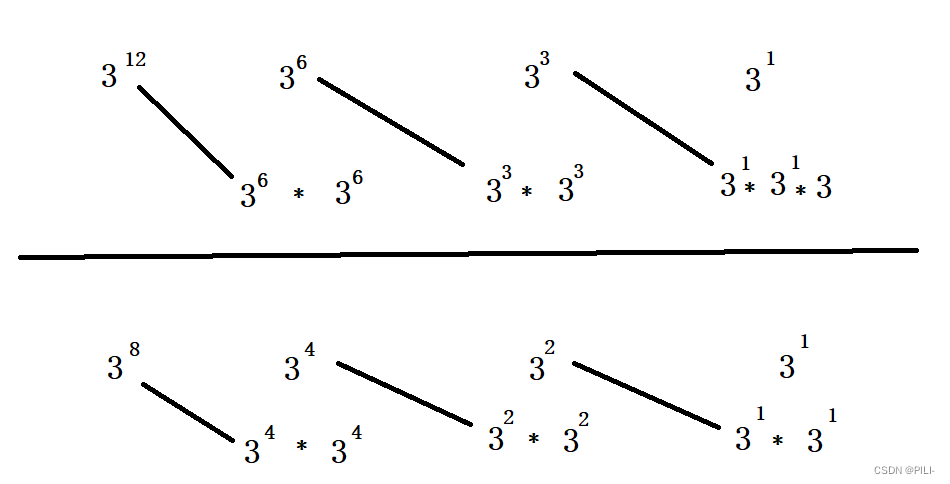
 从中也可以发现，每个轮回，都是相同的子问题；

1. 重复子问题 -> 函数头：给定一个数 x ，要求其 n 次幂，返回结果；

2. 解析子问题 -> 函数体：x 的 n 次幂等于两个 x 的 n/2 次幂 进行相乘，还要进行判断，判断 n%2 是否为 0 ，如果为 0，则为情况 2，如果为 1，则为情况 1，就需要再乘一次 x；

3. 递归出口：当 n == 0 的时候，return 1；

还有一个注意点：就是 n 可以为负数，此时 x 的 n 次幂就等于 x 的 -n 次幂 的倒数； 

代码实现：

class Solution {
    public double myPow(double x, int n) {
        return n < 0 ? 1.0 / Pow(x,-n) : Pow(x,n);
    }
    public double Pow(double x,int n){
        if(n == 0) return 1;
        double ret = Pow(x,n/2);
        return n % 2 == 0 ? ret * ret : ret * ret * x; 
    }
}