[动态规划] (十二) 简单多状态: LeetCode 213.打家劫舍II

213. 打家劫舍 II

题目解析

本题是对打家劫舍和按摩师的升级题型，可以看完上一道题再来看下面的内容。

[动态规划] (十一) 简单多状态 LeetCode 面试题17.16.按摩师 和 198.打家劫舍-CSDN博客

(1) 房屋是环绕的，第一个房子和最后一个房子是紧挨着的

(2) 不能连续进入房子

(3) 返回最高金额

解题思路

状态表示

dp[i]：按照以往的经验，以i为结尾可以获得的最高的金额。

dp[i]又可以分为偷到i位置时，进入i房间(f[i])和不进入i房间(g[i])。(详情可以点之前的链接。)

但是本题又不一样，多了个房屋环绕，如图。

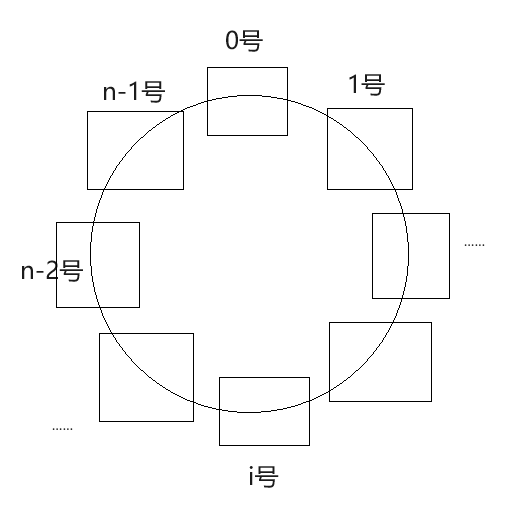
由于0号房间和n-1号房间是紧挨的，我们只能进入其中一个。

所以细分问题为：进入0号房或者不进入0号房。

• 进入0号房

如果偷了0号房，那么我们首先就不能再进入1号，和n-1号。

剩下的2_{n-2号就是一个打家劫舍I的子问题：从2}n-2号进行打家劫舍I。

• 不进入0号房

如果不进入了0号房，那么我们可以划分1_{n-1号房为打家劫舍I的子问题，从1}n-1号房进行打家劫舍I。

状态转移方程

和打家劫舍I一样。

• f[i]

进入i号房间就不能进入i-1号房间。(与打家劫舍I、按摩师分析相同)

f[i] = g[i-1] + nums[i]

• g[i]

不进入i号房，就要选择进入或者不进入i-1号房。(与打家劫舍I、按摩师分析相同)

g[i] = max(f[i-1], g[i-1])

初始化和填表顺序

• 初始化

(与打家劫舍I、按摩师分析相同)

f[0] = nums[0], g[0] = 0;

• 填表顺序

(与打家劫舍I、按摩师分析相同)

从左向右填表即可。

返回值

(与打家劫舍I、按摩师分析相同)

返回较大的那个金额即可。

提醒

仅仅是对问题进行分类，实际上还是打家劫舍I(按摩师)问题。

看到这里就可以去尝试实现代码了，然后再看下面的内容。

---

代码实现

class Solution {
public:
    int rob1(vector<int>& nums, int left, int right)
    {
        if(left > right) return 0;
        //创建dp数组
        int n = nums.size();
        vector<int> f(n);
        vector<int> g(n);
        //初始化
        f[left] = nums[left];
        //填表
        for(int i = left+1; i <= right; i++)
        {
            f[i] = g[i-1] + nums[i];
            g[i] = max(f[i-1], g[i-1]);
        }
        //返回值
        return max(f[right], g[right]);
    }
    int rob(vector<int>& nums) {
        int n = nums.size();
       return max(nums[0] + rob1(nums, 2, n-2), rob1(nums, 1, n-1));
    }
};

总结

细节1：本质上是进行打家劫舍I(按摩师)问题，只需要划分好区间即可。

细节2：注意，如果left>right时，还进行填表就没有意义了

细节3：初始化时，我们从传进来的位置left初始化即可，填表从传进来的left+1开始。

细节4：返回值是最后一个位置的元素即为max(f[right], g[right])

细节5：大家都不要学习偷窃这种行为。