蓝桥杯算法竞赛系列第九章·巧解哈希题，用这3种数据类型足矣

在这里插入图片描述

你好，我是安然无虞。

文章目录

哈希基础概念
哈希相关题目
- · 有效的字母异位词
- · 赎金信
- · 字母异位词分组
- · 两个数组的交集
- · 快乐数
- · 两数之和
- · 四数相加 II
- · 最长连续序列
- · 查找共用字符
- · 同构字符串
- · 单词规律
- · 字节跳动面试：缺失的第一个正数

哈喽哈喽，好久没总结完整的算法博客啦，今天开始把之前欠下的补上，一起加油哦。

在开肝之前，请老铁们思考一个问题：算法对于我们计算机相关专业的大学生来说重要吗，是“非常重要”，还是“狗都不学”，欢迎大家在评论区发表自己的看法。

首先从哈希表说起吧，因为我上次面试遇到这个题型了，还是TM hard（哭泣）。

OK，话不多说，开车～

哈希基础概念

常用作哈希表的三种数据结构：

数组
set
map

数组的话就不多说了，下面我们来谈谈set和map：

首先来说说unordered_set和set以及multiset的区别：

unordered_set底层实现是哈希表，set和multiset的底层是红黑树，而红黑树是一种平衡二叉搜索树，所以key是有序的，但是key不可以修改，因为改动key会导致整棵树的错乱，所以只能删除或者增加。

具体如下表：

集合	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
set	红黑树	有序	否	否	O(logN)	O(logN)
multiset	红黑树	有序	是	否	O(logN)	O(logN)
unordered_set	哈希表	无序	否	否	O(1)	O(1)

接下来谈谈unordered_map和map以及multimap的区别：

unordered_map底层实现是哈希表，map和multimap的底层是红黑树，而红黑树是一种平衡二叉搜索树，同理map和multimap的key也是有序的。

映射	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
map	红黑树	key有序	key不可重复	key不可修改	O(logN)	O(logN)
multimap	红黑树	key有序	key可重复	key不可修改	O(logN)	O(logN)
unordered_map	哈希表	key无序	key不可重复	key不可修改	O(1)	O(1)

所以当我们要使用集合来解决哈希问题的时候，优先使用unordered_set，因为它的查询和增删效率都是最优的，如果要求集合是有序的，那么就使用set，如果要求集合不仅有序，还要有重复数值，那么就使用multiset。

map是一个<key, value>的数据结构，map对key是有限制的，因为其不可以修改，对value是没有限制的，因为key的存储方式是使用红黑树实现的。

但是哈希法是牺牲空间换取了时间，因为我们要使用额外的数组、set或者map来存放数据，才能实现快速的查找。

当遇到需要判断一个元素是否在集合中出现过的场景，就应该第一时间想到哈希法。

哈希相关题目

下面开始我们刷题之旅，在刷题中探索算法的奥秘～

· 有效的字母异位词

题目链接：有效的字母异位词

在这里插入图片描述

解题思路：

首先我们看到字符串s和t都只包含小写字母，所以我们可以定义一个整数数组用于统计字符串中每个字符的出现次数。

先遍历字符串s统计其中每个字符的出现次数；
紧接着再遍历字符串t用哈希数组中统计的s字符串中字符出现次数减去t中出现次数；
最后再遍历哈希数组，如果数组中每个元素都是0就是有效字母异位词。

代码详解：

class Solution {
public:
    bool isAnagram(string s, string t) 
    {
        // 定义一个数组用来统计每个字符的出现次数
        int hashNums[26] = {0};

        // 遍历字符串s统计每个字符的出现次数
        for(int i = 0; i < s.size(); i++)
        {
            hashNums[s[i] - 'a']++;
        }

        // 遍历字符串t用哈希数组中统计的字符出现次数减去t中出现次数
        for(int i = 0; i < t.size(); i++)
        {
            hashNums[t[i] - 'a']--;
        }

        // 最后再遍历哈希数组，如果都为0就符合题意
        for(int i = 0; i < 26; i++)
        {
            if(hashNums[i] != 0)
            {
                return false;
            }
        }

        return true;
    }
};

// 思路2:
// 1. 分别统计每个字符串中的字符出现次数
// 2. 判断两个字符串中所有字符出现次数是否相等
class Solution {
public:
    bool isAnagram(string s, string t) 
    {
        vector<int> nums1 = encode(s);
        vector<int> nums2 = encode(t);

        // 判断两个字符串中所有字符出现次数是否相等
        for(int i = 0; i < 26; i++)
        {
            if(nums1[i] != nums2[i])
            {
                return false;
            }
        }

        return true;
    }

    // 统计字符串中字符的出现次数
    vector<int> encode(string& s)
    {
        vector<int> hashNums(26);

        for(int i = 0; i < s.size(); i++)
        {
            hashNums[s[i] - 'a']++;
        }

        return hashNums;
    }
};

· 赎金信

题目链接：赎金信

在这里插入图片描述

解题思路：

本题跟上一道题很类似，只不过可能需要注意一下对于细节的处理，这里就不多说了，请老铁细品。

代码详解：

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) 
    {
        vector<int> hashNums(26);

        // 先统计字符串magazine中字符的出现次数
        for(int i = 0; i < magazine.size(); i++)
        {
            hashNums[magazine[i] - 'a']++;
        }

        // 遍历字符串ransomNote用哈希数组中统计的字符出现次数减去其中出现次数
        for(int i = 0; i < ransomNote.size(); i++)
        {
            hashNums[ransomNote[i] - 'a']--;

            if(hashNums[ransomNote[i] - 'a'] < 0)
                return false;
        }

        return true;
    }
};

· 字母异位词分组

题目链接：字母异位词分组

在这里插入图片描述

解题思路：参考：《la bu la dong》

本题也是异位词相关，异位词这类问题的关键在于，如何迅速判断两个字符串是异位词，主要考察我们数据编码和哈希表的使用：

是否可以找到一种编码方法，使得字母异位词的编码都相同？找到这种编码方式之后，就可以用一个哈希表存储编码相同的所有异位词，得到最终的答案。

242. 有效的字母异位词考察了异位词的编码问题，对字符串排序可以是一种编码方案，如果是异位词，排序后就变成一样的了，但是这样时间复杂度略高，且会修改原始数据。更好的编码方案是利用每个字符的出现次数进行编码，也就是下面的解法代码。

代码详解：

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) 
    {
        // 建立编码到分组的映射
        unordered_map<string, vector<string>> encodeToGroup;

        // 将相同编码的字符串放到一个分组中
        for(auto& str : strs)
        {
            // 对字符串进行编码
            string code = encode(str);

            // 将相同编码的字符串放到一起
            encodeToGroup[code].push_back(str);
        }

        // 统计结果
        vector<vector<string>> res;
        for(auto& group : encodeToGroup)
        {
            res.push_back(group.second);
        }

        return res;
    }

    // 对字符串中字符的出现次数进行编码
    string encode(string& s)
    {
        vector<int> hashNums(26);

        for(int i = 0; i < s.size(); i++)
        {
            hashNums[s[i] - 'a']++;
        }

        string code(hashNums.begin(), hashNums.end());

        return code;
    }
};

· 两个数组的交集

题目链接：两个数组的交集

在这里插入图片描述

解题思路：

统计两个数组的交集，而且要保证结果中每个元素都是唯一的，所以第一时间想到的是set相关结构。

然后本题很简单，有不理解的地方直接看代码注释就行啦。

代码详解：

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) 
    {
        // 将nums1中数字存放到集合中
        unordered_set<int> set;
        for(int num : nums1)
        {
            set.insert(num);
        }

        // 记录结果
        unordered_set<int> res;

        // 遍历数组2进行比较，统计结果
        for(int num : nums2)
        {
            if(set.count(num))
            {
                res.insert(num);
            }
        }

        return vector<int>(res.begin(), res.end());
    }
};

· 快乐数

题目链接：快乐数

在这里插入图片描述

解题思路：

题目中说了会 无限循环，那么也就是说求和的过程中，sum会重复出现，这对解题很重要！

当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。

所以这道题目使用哈希法，来判断这个sum是否重复出现，如果重复了就是return false，否则一直找到sum为1为止。

代码详解：

class Solution {
public:

    // 统计数字的每一位的平方和 - 101
    int getNum(int n)
    {
        int sum = 0;

        while(n != 0)
        {
            sum += (n % 10) * (n % 10);
            n /= 10;
        }

        return sum;
    }

    bool isHappy(int n) 
    {
        // 将计算结果记录到集合当中
        unordered_set<int> set;

        while(n != 1)
        {
            int num = getNum(n);

            if(set.count(num))
            {
                return false;
            }
            else
            {
                set.insert(num);
            }

            n = num;
        }

        return true;
    }
};

· 两数之和

题目链接：两数之和

在这里插入图片描述

解题思路：

对于一个元素 nums[i]，想知道有没有另一个元素 nums[j] 的值为 target - nums[i]，这很简单，我们用一个哈希表记录每个元素的值到索引的映射，这样就能快速判断数组中是否有一个值为 target - nums[i] 的元素了。

简单说，数组其实可以理解为一个「索引 -> 值」的哈希表映射，而我们又建立一个「值 -> 索引」的映射即可完成此题。

代码详解：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) 
    {
        // 建立值到索引的映射
        unordered_map<int, int> valToIndex;

        for(int i = 0; i < nums.size(); i++)
        {
            // 查哈希表，看是否有能和 nums[i] 凑出 target 的元素
            int need = target - nums[i];
            if(valToIndex.count(need))
            {
                return {i, valToIndex[need]};
            }

            // 存入val->index的映射
            valToIndex[nums[i]] = i;
        }    

        return {-1, -1};
    }
};

· 四数相加 II

题目链接：四数相加 II

在这里插入图片描述

解题思路：

首先定义一个unordered_map，key放a和b两数之和，value 放a和b两数之和出现的次数。
遍历大A和大B数组，统计两个数组元素之和，和出现的次数，放到map中。
定义int变量count，用来统计 a+b+c+d = 0 出现的次数。
在遍历大C和大D数组，找到如果 0-(c+d) 在map中出现过的话，就用count把map中key对应的value也就是出现次数统计出来。
最后返回统计值 count 就可以了

代码详解：

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        // 统计数组12所有元素的和及其出现次数
        unordered_map<int, int> sumToCount;
        for(int i = 0; i < nums1.size(); i++)
        {
            for(int j = 0; j < nums2.size(); j++)
            {
                int sum = nums1[i] + nums2[j];
                sumToCount[sum]++;
            }
        }

        // 记录符合题意的结果
        int count = 0;

        // 遍历数组34寻找符合条件的组合
        for(int i = 0; i < nums3.size(); i++)
        {
            for(int j = 0; j < nums4.size(); j++)
            {
                int sum = nums3[i] + nums4[j];
                if(sumToCount.count(0 - sum))
                {
                    count += sumToCount[0-sum];
                }
            }
        }

        return count;
    }
};

· 最长连续序列

题目链接：最长连续序列

在这里插入图片描述

解题思路：

这道题最直接的想法就是排序，排序之后连续的序列就很容易找到了。但是排序的时间复杂度是 O(NlogN)，而题目要求我们时间复杂度为 O(N)，所以我们需要另想办法。

想找连续序列，首先要找到这个连续序列的开头元素，然后递增，看看之后有多少个元素还在 nums 中，即可得到最长连续序列的长度了。

由此我们可以想到用空间换时间的思路，把数组元素放到哈希集合里面，然后去寻找连续序列的第一个元素，即可在 O(N) 时间找到答案。

比方说 nums = [8,4,9,1,3,2]，我们先找到 1，然后递增，找到了 2, 3, 4，这就是一个长度为 4 的序列。

代码详情：

class Solution {
public:
    int longestConsecutive(vector<int>& nums) 
    {
        // 转化成哈希集合，方便快速判断是否存在某个元素
        unordered_set<int> set;
        for (int num : nums) 
        {
            set.insert(num);
        }
				
      	// 记录结果
        int res = 0;

        for (int num : set) {
            if (set.count(num - 1)) {
                // num 不是连续子序列的第一个，跳过
                continue;
            }
            // num 是连续子序列的第一个，开始继续计算连续子序列的长度
            int curNum = num;
            int curLen = 1;

            while (set.count(curNum + 1)) {
                curNum += 1;
                curLen += 1;
            }
            // 更新最长连续序列的长度
            res = max(res, curLen);
        }

        return res;
    }
};

· 查找共用字符

题目链接：查找共用字符

在这里插入图片描述

解题思路：

我们先定义一个哈希数组记录第一个字符串中字符的出现次数
然后再定义一个哈希数组记录其他字符串中字符的出现次数，循环比较取两者较小值，请参考代码注释进行理解

代码详情：

class Solution {
public:
    vector<string> commonChars(vector<string>& words) 
    {
        // 记录结果
        vector<string> res;

        // 统计第一个字符串中字符的出现次数
        int hash[26] = {0};

        for(int i = 0; i < words[0].size(); i++)
        {
            hash[words[0][i] - 'a']++;
        }

        // 统计出第一个字符串之外的字符串中字符的出现次数
        int hashOther[26] = {0};
        
        for(int i = 1; i < words.size(); i++)
        {
            memset(hashOther, 0, sizeof(hashOther)); // 别忘记每次都要清空

            for(int j = 0; j < words[i].size(); j++)
            {
                hashOther[words[i][j] - 'a']++;
            }

            // 和第一个字符串比较，取较小值
            for(int i = 0; i < 26; i++)
            {
                hash[i] = min(hash[i], hashOther[i]);
            }
        }

        // 将哈希数组中元素不为0的转换为字符后插入到结果字符串中
        for(int i = 0; i < 26; i++)
        {
            // 注意理解为啥是while而不是if
            while(hash[i] != 0)
            {
                string str(1, i + 'a');
                res.push_back(str);
                hash[i]--;
            }
        }

        return res;
    }
};

· 同构字符串

题目链接：同构字符串

在这里插入图片描述

解题思路：

字符串没有说都是小写字母之类的，所以用数组不合适了，用map来做映射。

使用两个map 保存 s[i] 到 t[j] 和 t[j] 到 s[i] 的映射关系，如果发现对应不上，立刻返回 false

代码详解：

class Solution {
public:
    bool isIsomorphic(string s, string t) 
    {
        // 使用两个map来保存从s[i]到t[j]和从t[j]到s[i]的映射关系
        unordered_map<char, char> map1;
        unordered_map<char, char> map2;

        for(int i = 0, j = 0; i < s.size(); i++, j++)
        {
            if(map1.find(s[i]) == map1.end())
            {
                // map1保存着从s[i]到t[j]的映射
                map1[s[i]] = t[j];
            }

            if(map2.find(t[j]) == map2.end())
            {
                // map2保存着从t[j]到s[i]的映射
                map2[t[j]] = s[i];
            }
            
            // 发现映射 对应不上，立刻返回false
            if(map1[s[i]] != t[j] || map2[t[j]] != s[i])
                return false;
        }

        return true;
    }
};


// 思路2: 可以仿照单词规律的思路，请题请看下一题
class Solution {
public:
    bool isIsomorphic(string s, string t) 
    {
        if(s.size() != t.size())
        {
            return false;
        }

        unordered_map<char,char> map; // 建立字符到字符的映射
        unordered_set<char> hasWord; // 记录有字符映射字符

        for(int i = 0; i < s.size(); i++)
        {
            if(!map.count(s[i]))
            {
                if(hasWord.count(t[i]))
                {
                    return false;
                }

                map[s[i]] = t[i];
            }
            else
            {
                if(map[s[i]] != t[i])
                {
                    return false;
                }
            }

            hasWord.insert(t[i]);
        }

        return true;
    }
};

· 单词规律

题目链接：单词规律

在这里插入图片描述

解题思路：

利用哈希表，把 pattern 中的每个叠词模式字符在 s 中的对应单词记录下来，就能判断 s 是否匹配 pattern 的模式了。

具体请看代码详解：

class Solution {
public:
    bool wordPattern(string pattern, string s) 
    {
        vector<string> words;

        stringstream ss(s);
        string str;

        while(getline(ss, str, ' '))
        {
            words.push_back(str);
        }

        // 注意这一条判断语句，别忘记了
        if(pattern.size() != words.size())
        {
            return false;
        }

        // 建立字符到字符串的映射
        unordered_map<char, string> patternToStr;

        // 记录已经有字符对应的字符串
        unordered_set<string> hasWord;

        for(int i = 0; i < pattern.size(); i++)
        {
            char c = pattern[i]; 
            string word = words[i];

            // 该字符还没有建立对应的单词映射
            if(!patternToStr.count(c))
            {
                // 但是与之对应的单词却有自己的字符了
                if(hasWord.count(word))
                {
                    return false;
                }   

                // 建立该字符到单词的映射
                patternToStr[c] = word;
            }
            else // 该字符已经有对应的单词了
            {   
                // 如若该字符所对应的单词与实际不符
                if(patternToStr[c] != word)
                {
                    return false;
                }
            }

            hasWord.insert(word);
        }

        return true;
    }
};

· 字节跳动面试：缺失的第一个正数

题目链接：缺失的第一个正数

在这里插入图片描述

解题思路：

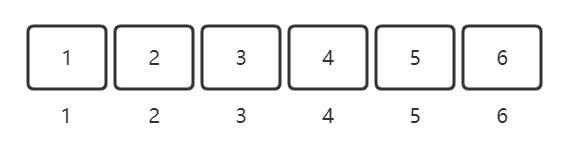
理想情况下每个元素都在自己的位置上，如下：

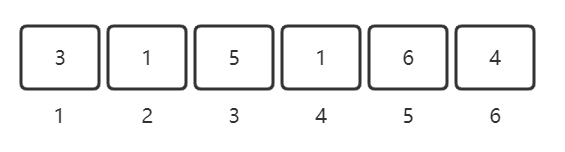
现在将元素对应位置打乱，并且缺失了一个元素，如下：

题目就是要求我们找到这个缺失的元素，我们该如何找呢？

注意：首先我们需要遍历数组中的每一个元素，比如nums[i]，我们将以nums[i]为下标的元素中的值置换为其绝对值的相反数，也就是做标记。（做这道题目的时候一定要画图来理解）

像下面这样：

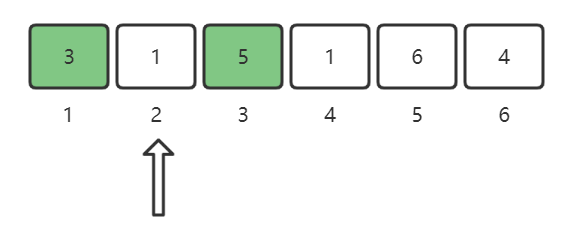
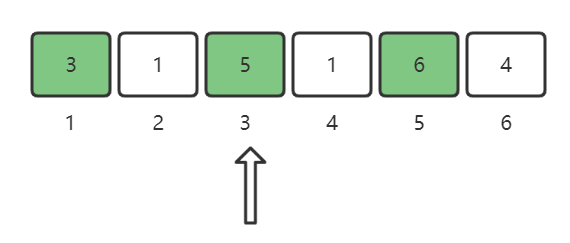
nums[1] = 3，将3这个位置做标记：

nums[2] = 1，将1这个位置做标记：

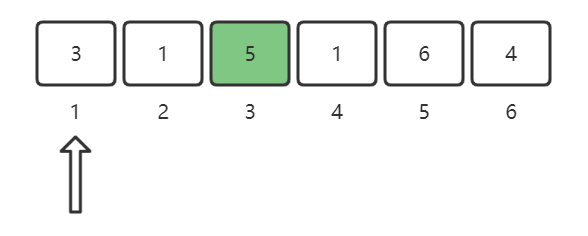
nums[3] = 5，将5这个位置做标记：

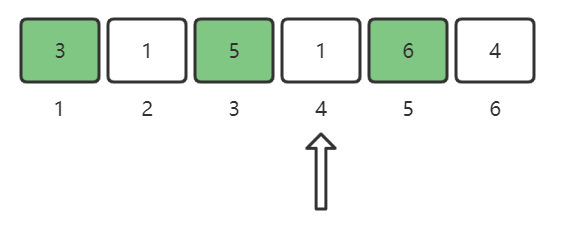
nums[4] = 1，将1这个位置做标记：

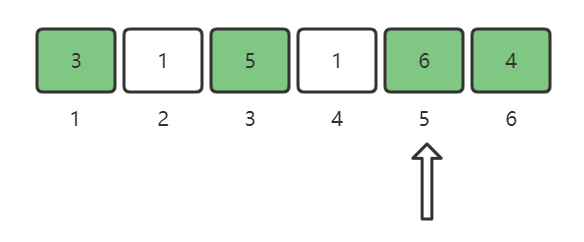
nums[5] = 6，将6这个位置做标记：

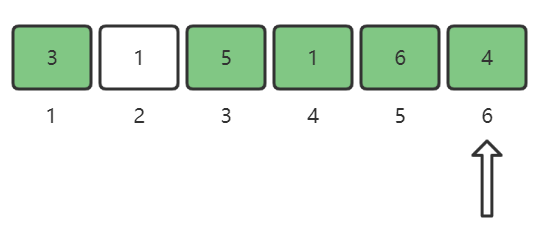
nums[6] = 4，将4这个位置做标记：

现在我们看到，只有2这个位置是没有做标记的，所以2就是所求。

温馨提示：可能比较难以理解，一定要自己动手画图去理解。

所以想到这一步的话，那么这道题目前的难点就是怎么做标记了，OK接着看：

首先，我们遍历数组将数组中值为非正整数的元素全部忽略，什么意思呢就是将其值全部映射到n之外，所以我们遍历一遍数组，将值为负数和值为0的元素全部赋值为n+1;

接下来就是，遍历数组中的每一个元素nums[i]，先判断其值是否大于n，若大于，则说明其之前是非正整数，忽略它，继续向后遍历；反之，则将以nums[i]为下标的值置换为其绝对值的相反数（因为可能有两个相同的元素，注意画图理解）。

最后再遍历数组中的每一个元素，值不为负数，其下标就是题目所求。

题目详解：

class Solution {
public:
    int firstMissingPositive(vector<int>& nums) 
    {   
        int n = nums.size();

        // 将数组中的非正整数元素忽略，即是映射到n之外
        for(int i = 0; i < n; i++)
        {
            if(nums[i] <= 0)
            {
                nums[i] = n + 1;
            }
        }

        // 遍历数组中的元素，将以元素的值为对应的下标里的元素取其绝对值的相反数，也就是做标记
        for(int i = 0; i < n; i++)
        {
            if(abs(nums[i]) <= n) // 说明是正整数
            {
                nums[abs(nums[i]) - 1] = -abs(nums[abs(nums[i]) - 1]);
            }
        }

        // 遍历数组中的元素，元素值不为负数的其下标就是答案
        for(int i = 0; i < n; i++)
        {
            if(nums[i] > 0)
            {
                return i + 1;
            }
        }

        return n + 1;
    }
};